Xavier初始值是以【激活函数是线性函数】为前提而推导出来的。

因sigmoid函数和tanh函数左右对称，且中央附近可以视作线性函数，所以适合使用 Xavier 初始值。但当激活函数使用 ReLU 时，一般推荐使用 ReLU 专用的初始值，也就是 Kaiming He 等人推荐的初始值，也称为“He 初始值”。当前一层的节点数为n时，He 初始值使用标准差为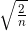的高斯分布。当 Xavier 初始值是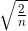时，（直观上）可以解释为，因为 ReLU 的负值区域的值为 0，为了使它更有广度，所以需要 2 倍的系数。

现在来看一下激活函数使用 ReLU 时激活值的分布。我们给出了 3 个实验的结果（图 6-14），依次是权重初始值为标准差是 0.01 的高斯分布（下文简写为“std = 0.01”）时、初始值为 Xavier 初始值时(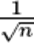)、初始值为 ReLU (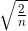)专用的“He 初始值”时的结果。

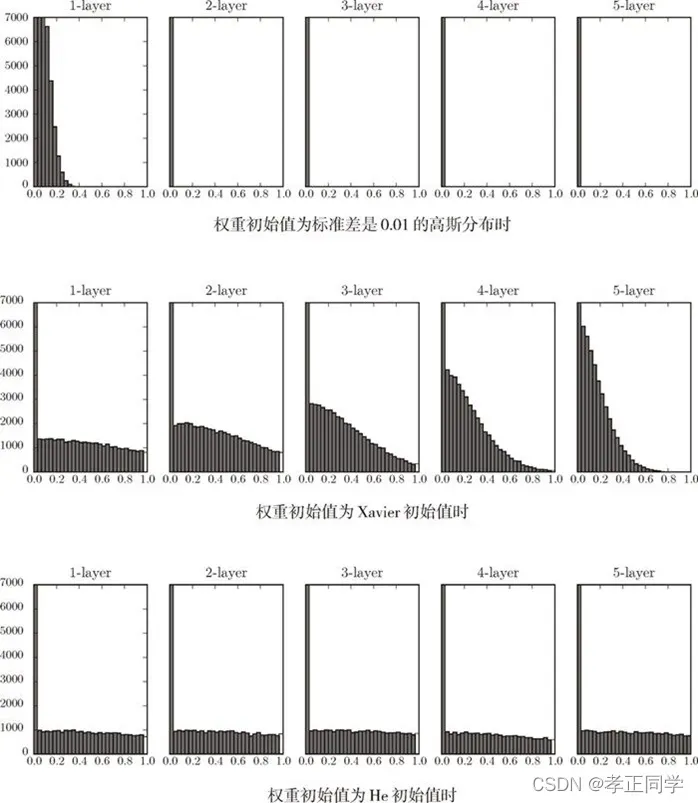
图 6-14　激活函数使用 ReLU 时，不同权重初始值的激活值分布的变化

观察实验结果可知，当“std = 0.01”时，各层的激活值非常小。例如此时各层激活值的分布平均值如下。1 层 : 0.0396，2 层 : 0.00290，3 层 : 0.000197，4 层 : 1.32e-5，5 层 : 9.46e-7。

神经网络传递的值非常小，表明反向传播期间权重的梯度也很小。这是一个严重的问题，实际上学习上基本没有进步。

接下来是初始值为 Xavier 初始值时的结果。在这种情况下，随着层的加深，偏向一点点变大(“偏向”意思是倾斜度)。实际上，层加深后，激活值的偏向变大，学习时会出现梯度消失的问题。而当初始值为 He 初始值时，各层中分布的广度相同。由于即便层加深，数据的广度也能保持不变，因此逆向传播时，也会传递合适的值。

综上所述，

1. 当激活函数使用 ReLU 时，权重初始值使用 He 初始值，
2. 当激活函数为 sigmoid 或 tanh 等 S 型曲线函数时，初始值使用 Xavier 初始值。这是目前的最佳实践。

附：图6-14代码

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1/(1+np.exp(-x))
x = np.random.randn(1000, 100)
node_num = 100
hidden_layer_size = 5
activations = {}

std = 1/np.sqrt(node_num)#从此处替换 权重的标准差
for i in range(hidden_layer_size):
    if i!=0:
        x = activations[i-1]
    w = np.random.randn(node_num, node_num) * std
    z = np.dot(x, w)
    a = sigmoid(z)
    activations[i] = a

#绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1)+'layers')
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()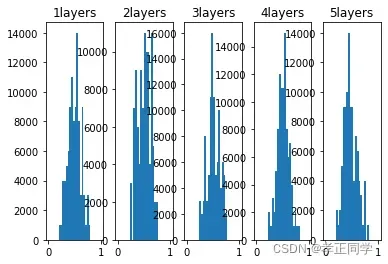

权重参数为1/sqrt(n)

基于MNIST数据集的权重初始化比较

下面通过实际的数据，观察不同的权重初始值的赋值方法会在多大程度上影响神经网络的学习。这里，我们基于 std = 0.01、Xavier 初始值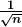（）、He 初始值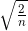（）进行实验。先来看一下结果，如图 6-15 所示。

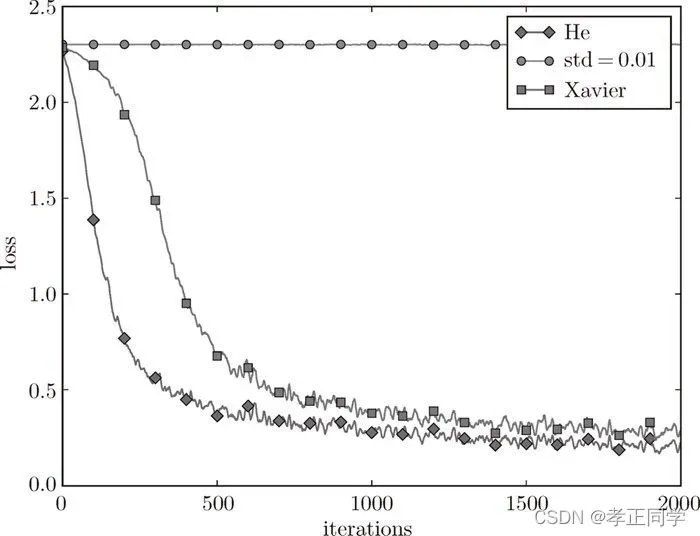
图 6-15　基于 MNIST 数据集的权重初始值的比较：横轴是学习的迭代次数（iterations），纵轴是损失函数的值（loss）

这个实验中，神经网络有 5 层，每层有 100 个神经元，激活函数使用的是 ReLU。

从图 6-15 的结果可知，std = 0.01 时完全无法进行学习。这和刚才观察到的激活值的分布一样，是因为正向传播中传递的值很小（集中在 0 附近的数据）。因此，逆向传播时求到的梯度也很小，权重几乎不进行更新。相反，当权重初始值为 Xavier 初始值和 He 初始值时，学习进行得很顺利。并且，我们发现 He 初始值时的学习进度更快一些。

综上所述，在神经网络的学习中，权重的初始值非常重要。在很多情况下，权重初始值的设置关系到神经网络学习的成功与否。