Lesson 3.3 线性回归手动实现与模型局限

• 补充知识点相关系数计算

# 科学计算模块
import numpy as np
import pandas as pd

# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt

# 自定义模块
from ML_basic_function import *

一、线性回归的手动实现

接下来，我们尝试进行线性回归模型的手动建模实验。建模过程将遵照机器学习的一般建模流程，并且借助NumPy所提供的相关工具来进行实现。通过本次实验，我们将进一步深化对机器学习建模流程的理解，并且也将进一步熟悉对编程基础工具的掌握。

1.根据机器学习建模流程构建线性回归模型

• Step 1.数据准备

首先是准备数据集。我们使用数据生成器创建一个扰动不太大的数据集：

# 设置随机数种子
np.random.seed(24)   

# 扰动项取值为0.01
features, labels = arrayGenReg(delta=0.01)

labels[:10]

array([[ 4.43811826],
       [ 1.375912  ],
       [ 0.30286597],
       [ 1.81970897],
       [-2.47783626],
       [ 0.47374318],
       [ 2.83085905],
       [-0.83695165],
       [ 2.84344069],
       [ 0.8176895 ]])

features

array([[ 1.32921217, -0.77003345,  1.        ],
       [-0.31628036, -0.99081039,  1.        ],
       [-1.07081626, -1.43871328,  1.        ],
       ...,
       [ 1.5507578 , -0.35986144,  1.        ],
       [-1.36267161, -0.61353562,  1.        ],
       [-1.44029131,  0.50439425,  1.        ]])

plt.plot(features[:,0],labels,'o')
plt.plot(features[:,1],labels,'ro')

w = np.linalg.inv(features.T.dot(features)).dot(features.T).dot(labels)
w

array([[ 1.99961892],
       [-0.99985281],
       [ 0.99970541]])

y_hat = features.dot(w)
y_hat[:10]

array([[ 4.42754333],
       [ 1.35792976],
       [ 0.29698247],
       [ 1.83264567],
       [-2.47201615],
       [ 0.46806169],
       [ 2.8184199 ],
       [-0.81254525],
       [ 2.84841913],
       [ 0.81582296]])

plt.plot(features[:,0],y_hat,'o')

其中，features也被称为特征矩阵、labels也被称为标签数组

• Step 2.模型选取

接下来，选择一个模型来对上述回归问题数据进行建模。这里我们选择一个带有截距项的多元线性回归方程进行建模。基本模型是：

令，，上式可写为

注，此处如果要构建一个不带截距项的模型，则可另X为原始特征矩阵带入进行建模。

• Step 3.构造损失函数

对于线性回归来说，我们可以参照SSE、MSE或者RMSE的计算过程构造损失函数。由于目前模型参数还只是隐式的值（在代码中并不显示），我们可以简单尝试，通过人工设置一组来计算SSE。

• 另为一组随机值，计算SSE

np.random.seed(24)
w = np.random.randn(3).reshape(-1, 1)
w

array([[ 1.32921217],
       [-0.77003345],
       [-0.31628036]])

此时模型的输出为：

y_hat = features.dot(w)
y_hat[:10]

array([[ 2.04347616],
       [ 0.02627308],
       [-0.63176501],
       [ 0.20623364],
       [-2.64718921],
       [-0.86880796],
       [ 0.88171608],
       [-1.61055557],
       [ 0.80113619],
       [-0.49279524]])

据此，根据公式，SSE计算结果为：

(labels - y_hat).T.dot(labels - y_hat)

array([[2093.52940481]])

# 计算MSE
(labels - y_hat).T.dot(labels - y_hat) / len(labels)

array([[2.0935294]])

labels[:10]

array([[ 4.43811826],
       [ 1.375912  ],
       [ 0.30286597],
       [ 1.81970897],
       [-2.47783626],
       [ 0.47374318],
       [ 2.83085905],
       [-0.83695165],
       [ 2.84344069],
       [ 0.8176895 ]])

可以看出，在当前参数值下，模型输出结果与真实结果相差甚远。

不过，为了后续快速计算SSE，我们可以将上述SSE计算过程封装为一个函数，令其在输入特征矩阵、标签数组和真实参数情况下即可输出SSE计算结果：

def SSELoss(X, w, y):
    """
    SSE计算函数
    
    :param X：输入数据的特征矩阵
    :param w：线性方程参数
    :param y：输入数据的标签数组
    :return SSE：返回对应数据集预测结果和真实结果的误差平方和 
    """
    y_hat = X.dot(w)
    SSE = (y - y_hat).T.dot(y - y_hat)
    return SSE

# 简单测试函数性能
SSELoss(features, w, labels)

array([[2093.52940481]])

实验结束后，需要将上述SSELoss函数写入ML_basic_function.py中。

• Step 4.利用最小二乘法求解损失函数

接下来，我们需要在SSELoss中找到一组最佳的参数取值，另模型预测结果和真实结果尽可能接近。此处我们利用Lesson 2中介绍的最小二乘法来进行求解，最小二乘法求解模型参数公式为：

值得注意的是，在求解最小二乘法的过程中，特征矩阵的叉积需要可逆，即必须有逆矩阵。我们可以通过计算它的行​​列式来判断这个条件是否满足：

np.linalg.det(features.T.dot(features))

967456500.179829

行列式不为0，因此逆矩阵存在，可以通过最小二乘法求解。具体求解方法分为两种，其一是使用NumPy中线性代数基本方法，根据上述公式进行求解，同时也可以直接使用lstsq函数进行求解。

• 基本方法解决方案

w = np.linalg.inv(features.T.dot(features)).dot(features.T).dot(labels)
w

array([[ 1.99961892],
       [-0.99985281],
       [ 0.99970541]])

即可算出模型最优参数w。所谓模型最优参数，指的是参数取得任何其他数值，模型评估结果都不如该组参数时计算结果更好。首先，我们也可以计算此时模型SSE指标：

SSELoss(features, w, labels)

array([[0.09300731]])

明显小于此前所采用的随机w取值时SSE结果。此外，我们还可以计算模型MSE

SSELoss(features, w, labels) / len(labels)

array([[9.30073138e-05]])

当然，由于数据集本身是按照规则构建的，从模型参数上也可以看出模型预测效果更好。

模型评估指标中SSE、MSE、RMSE三者反应的是一个事实，我们根据SSE构建损失函数只是因为SSE计算函数能够非常方便的进行最小值推导，SSE取得最小值时MSE、RMSE也取得最小值。

• lstsq函数求解

当然，我们也可以利用lstsq函数进行最小二乘法结果求解。二者结果一致。

np.linalg.lstsq(features, labels, rcond=-1)

(array([[ 1.99961892],
        [-0.99985281],
        [ 0.99970541]]),
 array([0.09300731]),
 3,
 array([32.70582436, 31.3166949 , 30.3678959 ]))

最终w参数取值为：

np.linalg.lstsq(features, labels, rcond=-1)[0]

array([[ 1.99961892],
       [-0.99985281],
       [ 0.99970541]])

至此，我们已经完成了整个线性回归机器学习建模过程。

2. 线性回归模型的局限性

虽然上述建模过程可以发现，面对白噪声低、线性相关性明显的数据集，模型的整体表现较好，但在实际应用中，大部分数据集可能没有明显的线性相关性。 ，并且存在一定量的白噪声（数据错误）。这时，多元线性回归模型的效果会受到很大影响。

y_hat = features.dot(w)
y_hat[:10]

array([[ 4.42754333],
       [ 1.35792976],
       [ 0.29698247],
       [ 1.83264567],
       [-2.47201615],
       [ 0.46806169],
       [ 2.8184199 ],
       [-0.81254525],
       [ 2.84841913],
       [ 0.81582296]])

plt.plot(features[:, 0], labels, 'o')
# plt.plot(features[:, 0], y_hat, 'r-')

• 非线性相关律

例如，创建一个满足基本定律且白噪声极少的数据集，用于建模测试

# 设置随机数种子
np.random.seed(24)   

# 扰动项取值为0.01
features, labels = arrayGenReg(w=[3,1], deg=3, delta=0.01)

features

array([[ 1.32921217,  1.        ],
       [-0.77003345,  1.        ],
       [-0.31628036,  1.        ],
       ...,
       [ 0.84682091,  1.        ],
       [ 1.73889649,  1.        ],
       [ 1.93991673,  1.        ]])

plt.plot(features[:, 0], labels, 'o')

[<matplotlib.lines.Line2D at 0x27eaa6f5ac0>]

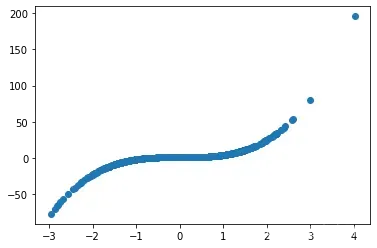
执行最小二乘模型参数求解

np.linalg.lstsq(features, labels, rcond=-1)

(array([[8.87909963],
        [0.95468493]]),
 array([64046.31887045]),
 2,
 array([32.13187164, 31.53261742]))

w = np.linalg.lstsq(features, labels, rcond=-1)[0]

w

array([[8.87909963],
       [0.95468493]])

SSELoss(features, w, labels)

array([[64046.31887045]])

y_hat = features.dot(w)

y_hat[:10]

array([[ 12.75689224],
       [ -5.8825188 ],
       [ -1.85359989],
       [ -7.8428192 ],
       [ -8.55319928],
       [-11.81979361],
       [  5.96619839],
       [  3.58042904],
       [-13.48632029],
       [  2.90422621]])

plt.plot(features[:, 0], labels, 'o')
plt.plot(features[:, 0], y_hat, 'r-')

[<matplotlib.lines.Line2D at 0x27eaa756d60>]

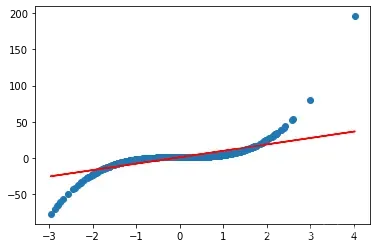
从模型结果可以看出，模型与数据集的分布规律存在较大差异。

• 噪音增加

另外，我们稍微增加模型的白噪声来测试线性回归模型的效果

# 设置随机数种子
np.random.seed(24)   

# 扰动项取值为2
features, labels = arrayGenReg(w=[2,1], delta=2)

features

array([[ 1.32921217,  1.        ],
       [-0.77003345,  1.        ],
       [-0.31628036,  1.        ],
       ...,
       [ 0.84682091,  1.        ],
       [ 1.73889649,  1.        ],
       [ 1.93991673,  1.        ]])

plt.plot(features[:, 0], labels, 'o')

np.linalg.lstsq(features, labels, rcond=-1)

(array([[1.91605821],
        [0.90602215]]),
 array([3767.12804359]),
 2,
 array([32.13187164, 31.53261742]))

w = np.linalg.lstsq(features, labels, rcond=-1)[0]

w

array([[1.91605821],
       [0.90602215]])

SSELoss(features, w, labels)

array([[3767.12804359]])

X = np.linspace(-5, 5, 1000)
y = w[0] * X + w[1]

plt.plot(features[:, 0], labels, 'o')
plt.plot(X, y, 'r-')

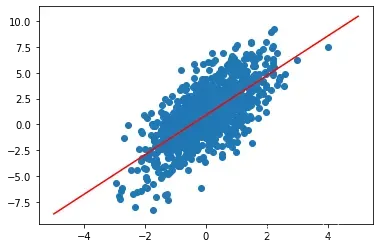
可以发现模型误差很大。

• 最小二乘条件限制

并且，除此之外，线性回归模型还面临这样一个重大问题，即如果特征矩阵的叉积不可逆，则最小二乘求解过程不成立。

当然，这也意味着数据集具有严重的多重共线性，也就是说，数据集的特征矩阵之间可能是线性表示的。此时，矩阵方程不一定有唯一解。有很多方法可以解决这个问题。从数学的角度，我们可以从以下三个方面入手：

• 首先，降低数据的维度：
  首先，可考虑进一步对数据集进行SVD分解或PCA主成分分析，在SVD或PCA执行的过程中会对数据集进行正交变换，最终所得数据集各列将不存在任何相关性。当然此举会对数据集的结构进行改变，且各列特征变得不可解释。
• 二、修改求解损失函数的方法：
  我们可以尝试求解原方程的广义逆矩阵。对于一些矩阵方程，通过求解广义逆矩阵，也可以得到近似最优解；此外，我们还可以使用梯度下降等其他优化方法。等待解决；
• 三、修改损失函数：
  其实可以修改原损失函数，令其满足最小二乘法求解条件即可。如果不可逆，那么我们可以通过试图在损失函数中加入一个正则化项，从而令损失函数可解。根据Lesson 2中的公式推导，目前根据SSE所构建的损失函数如下：

通过数学过程可以证明，此时如果我们在原有损失函数基础上添加一个关于参数的1-范数()或者2-范数()的某个计算结果，则可令最小二乘法条件得到满足。此时最小二乘法计算结果由无偏估计变为有偏估计。例如，当我们在损失函数中加上（其中为参数）时，模型损失函数为：

经数学变换后，可从导出上述矩阵表达式并将其置零，则可解出：

其中是单位矩阵。此时，由于肯定是一个可逆矩阵，所以可以顺利求解：

该过程也被称为岭回归。而类似的，如果是通过添加了的1-范数的某个表达式，从而构造损失函数如下：

则该过程被称为Lasso。而更进一步，如果构建的损失函数同时包含的1-范数和2-范数，形如如下形式：

则构建的是弹性网模型（Elastic-Net），其中都是参数，n是样本个数。不难发现，岭回归和Lasso其实都是弹性网的一种特殊形式。更多关于线性模型的相关方法，我们将在后续逐渐介绍。

1-范数也被称为L1范数，将参数的1-范数添加入损失函数的做法，也被称为损失函数的L1正则化，L2正则化也类似。在大多数情况下，添加正则化项也可称为添加惩罚函数，核心作用是缓解模型过拟合倾向。

三、线性回归的确定系数

对于线性回归模型来说，除了SSE以外，我们还可使用决定系数（R-square，也被称为拟合优度检验）作为其模型评估指标。决定系数的计算需要使用之前介绍的组间误差平方和和离差平方和的概念。在回归分析中，SSR表示聚类中类似的组间平方和概念，表意为Sum of squares of the regression，由预测数据与标签均值之间差值的平方和计算的出：

而SST（Total sum of squares）则是实际值和均值之间的差值的平方和计算得到：

并且，可以通过来计算。决定系数由和共同决定：

很明显，决定系数是一个鉴于[0,1]之间的值，并且约趋近于1，模型拟合效果越好。我们可以通过如下过程，进行决定系数的计算：

sst = np.power(labels - labels.mean(), 2).sum()
sse = SSELoss(features, w, labels)

r = 1-(sse/sst)

r

array([[0.50011461]])