上一篇文章中提到的贝叶斯推理的一般步骤是:
- 结合总体、样本和先验信息,得到参数贝叶斯后验分布
- 数据后验预测分布
,相对于先验预测分布
,后验预测分布增加了样本信息,因此更接近真实的预测分布。
- 通过适当提取后验预测分布
,可以得到后验预测均值
和后验预测方差
第二步和第三步都有积分计算,一般很难得到解析解。获得近似解的方法有两种,即蒙特卡洛采样法和变分推断法。
蒙特卡罗抽样
蒙特卡洛抽样是一种从目标分布中抽取样本,然后使用样本代替分布进行相关性计算的方法。该方法解决问题的基本步骤是:
- 构造一个概率模型,使得要解决的问题正好是概率模型的一个参数,比如概率模型的期望值
- 根据构建的概率模型生成样本
- 从样本中构建一个估计器并给出问题的近似解
例如求解积分,如果难以直接求解,可以通过蒙特卡洛采样法求解:
- 目标积分其实等价于
,这里我们先构造概率模型
- 然后从分布
中抽取几个样本
,将样本带入函数
得到
- 计算样本均值
作为积分问题的近似解
如果用蒙特卡洛抽样法求解,
用于表示样本
或以下描述中样本的充分统计量
,
表示特征,
表示要估计的值:
当我们对似然度建模时,我们一般对期望值进行建模,例如线性回归建模:
同时评估两边的条件分布给出:
或者我们将神经网络的输出采样为高斯分布的平均值:
于是上面的公式就变成了:
其中是从
分布中采样的几个参数。
如果我们能从中取样,问题就可以解决。考虑下面的抽样问题。
拒绝抽样
假设目标抽样分布为,是一个比较复杂的分布,直接抽样并不容易。并且目标分布可能没有被归一化,用
表示:
但我们可以从另外一个容易采样的分布中采样,比如高斯分布,这个分布称为Proposal分布。我对们
分布乘以常数系数k,使得下面不等式恒成立:
拒绝抽样的步骤是:
- 从
分布中抽样得到样本
- 以概率
丢弃样本
,或以概率
接受样本
- 重复以上2步骤,到样本容量满足要求为止
样本的真实概率为,等于目标分布乘以一个不影响数据分布的常数系数,采样得到的样本服从目标分布
。
下面是一个完整的例子,假设目标分布是混合高斯分布:
采用的proposal分布为标准高斯分布
参数系数的推导如下:
以下是示例实现代码:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
def gaussian_pdf(x, mu, sigma):
return tf.compat.v1.distributions.Normal(mu,sigma).prob(x)
def p_pdf(x):
# target distribution
return gaussian_pdf(x, 1.0, 0.5) + gaussian_pdf(x, 0.0, 1.0)
def q_pdf(x):
# proposal distribution
return gaussian_pdf(x, 0.0, 1.0)
def accept_rate(x):
k = 2 * np.exp(2.0/3.0) + 1
return p_pdf(x) / (k * q_pdf(x))
X = []
AC =[]
while len(X) < 2000:
x = np.random.normal(0.0, 1.0, 1)
ar = accept_rate(x)
AC.append(ar)
if tf.random.uniform([1]) < ar:
X.append(x)
Y.append(p_x)
r += 1
plt.plot(AC)
plt.grid()
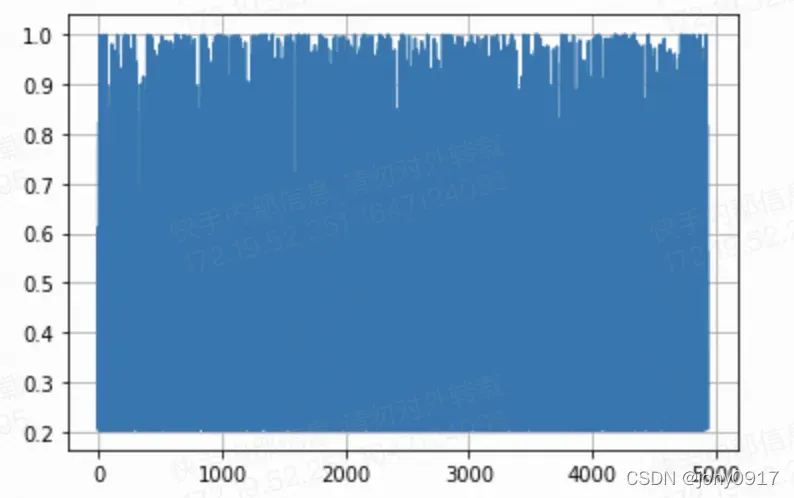
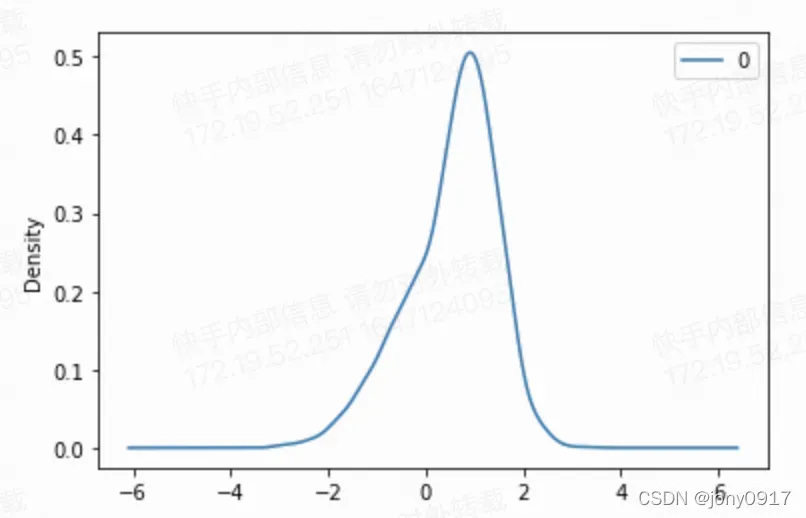
import pandas as pd
pd.DataFrame(X).plot(kind='density')

重要性抽样
目标积分分解如下:
可以看出,将中采样的样本
带入函数
后,乘以权重
即可得到目标结果。拒绝采样和重要性采样都需要proposal distribution和目标分布越接近越好。
如何解决概率归一化问题:
归一化问题解决了。
MCMC(马尔科夫链蒙特卡洛采样)
这里介绍称为M-H的MCMC采样算法,算法步骤为:
- 选择一个我们已经可以采样的分布(例如高斯分布)作为齐次马尔可夫链的转移概率:
- 以任意方式获取初始样本
,确定超参数
- 根据转移概率
和当前状态
,采样下一个状态
,以概率
接受新状态,如果接受新状态,则
,否则
- 重复第三步,选择
后的样本作为采样结果
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
def gaussian_pdf(x, mu, sigma):
return tf.compat.v1.distributions.Normal(mu,sigma).prob(x)
def p_pdf(x):
# target distribution
return gaussian_pdf(x, 1.0, 0.5) + gaussian_pdf(x, 0.0, 1.0)
def accept_rate(x_i, x_j):
t1 = p_pdf(x_j) * gaussian_pdf(x_j - x_i, 0.0, 0.1)
t2 = p_pdf(x_i) * gaussian_pdf(x_i - x_j, 0.0, 0.1)
ac_rate = t1 / t2
return min(1.0, ac_rate)
X = []
AC = []
M = 1000
x_i = 0.0
x_j = 0.0
r = 0
while len(X) < 1000:
x_j = x_i + np.random.normal(0.0, 0.1, 1)
ac = accept_rate(x_i, x_j)
AC.append(ac)
if tf.random.uniform([1]) < ac:
x_i = x_j
if r > M:
X.append(x_i)
r += 1
plt.plot(AC)
plt.grid()
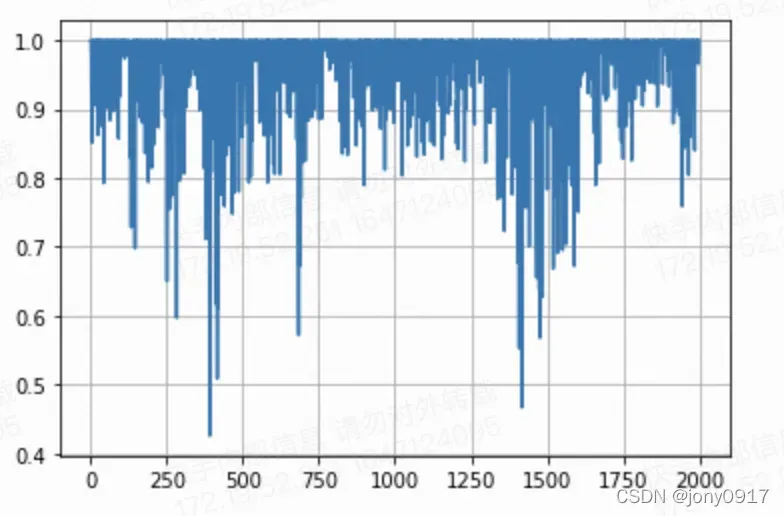
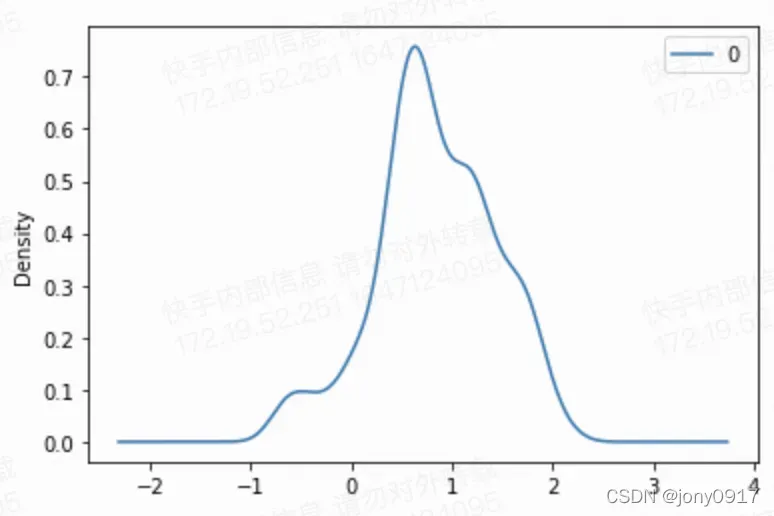
import pandas as pd
pd.DataFrame(X).plot(kind='density')
变分推理
变分推断的方式是寻找一个与目标分接近的参数分布,具体做法可以通过优化
与目标分布间的KL相散度:
定义了Loss后,可以通过梯度下降的方式寻找参数,下面是具体实现代码,任然一上面的混合高斯分布为目标分布,这里采用
,作为相似分布:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.optimizers import Adam
def gaussian_pdf(x, mu, sigma):
return tf.compat.v1.distributions.Normal(mu,sigma).prob(x)
def p_pdf(x):
# target distribution
return gaussian_pdf(x, 1.0, 0.5) + gaussian_pdf(x, 0.0, 1.0)
# 训练参数 w = {x_mu, x_rho}
x_mu = tf.Variable(0.0)
x_rho = tf.Variable(0.1)
trainables = [x_mu, x_rho]
x = x_mu + x_rho * tf.random.normal(x_mu.shape)
loss = tf.math.log(gaussian_pdf(x, x_mu, x_rho)) - tf.math.log(p_pdf(x))
r = 0
mus = []
rhos = []
losses = []
optimizer = Adam(0.0001)
while r < 20000:
with tf.GradientTape() as g:
x = x_mu + x_rho * tf.random.normal(x_mu.shape)
loss = tf.math.log(gaussian_pdf(x, x_mu, x_rho)) - tf.math.log(p_pdf(x))
gradients = g.gradient(loss, trainables)
optimizer.apply_gradients(zip(gradients, trainables))
losses.append(loss.numpy())
mus.append(x_mu.numpy())
rhos.append(x_rho.numpy())
r += 1
# 打印loss
plt.plot(losses)
plt.grid()
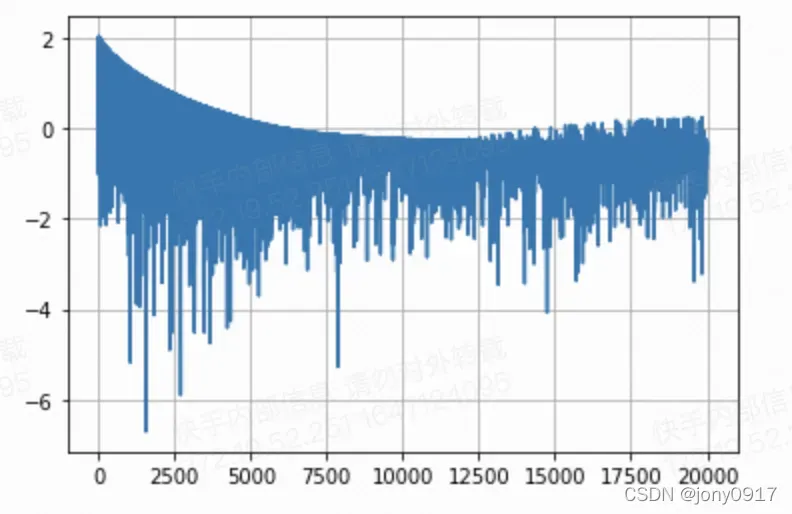
# 打印均值变化
plt.plot(mus)
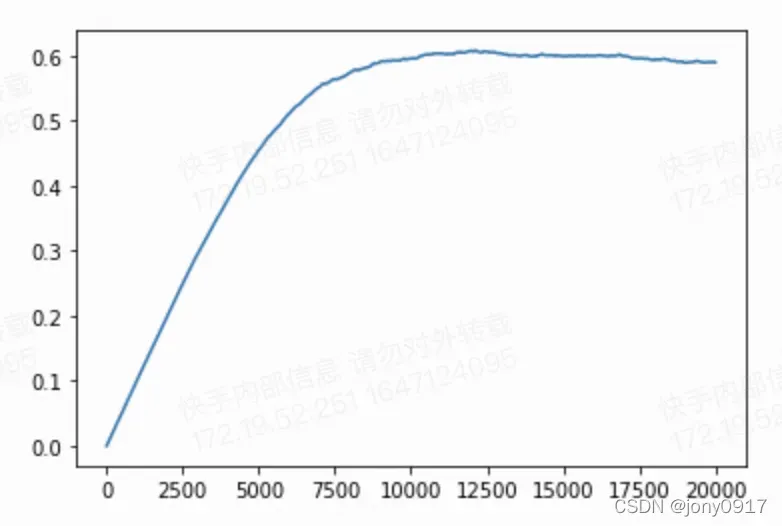
# 打印标准差变化
plt.plot(rhos)
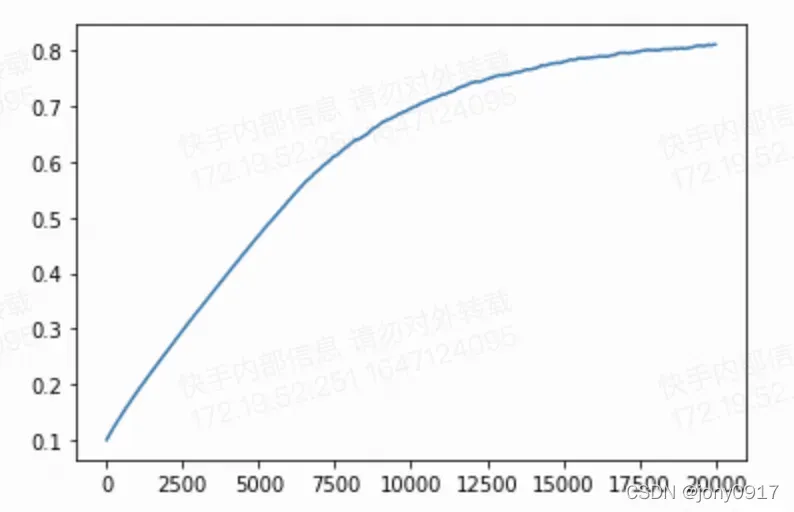
import pandas as pd
# 从训练完的分布q(x;w)中采样若干样本x
r = 0
X = []
Y = []
while r < 1000:
x = x_mu + x_rho * tf.random.normal(x_mu.shape)
p_x = gaussian_pdf(x, x_mu, x_rho)
X.append(x.numpy())
Y.append(p_x)
r += 1
pd.DataFrame(X).plot(kind='density')
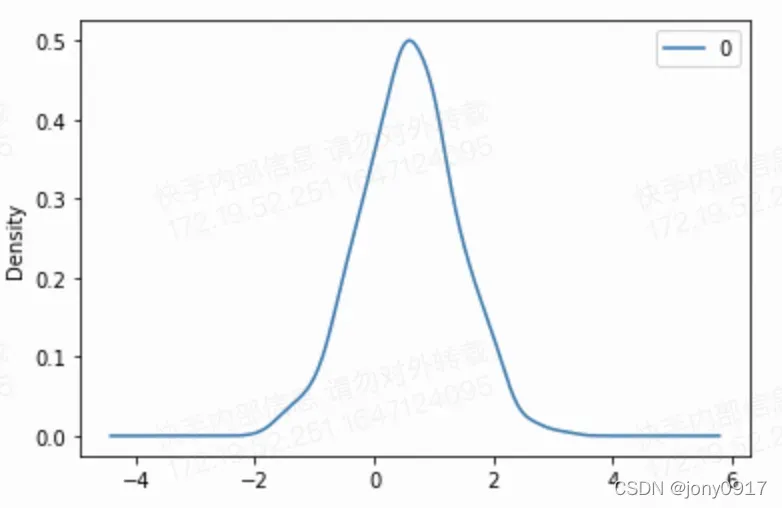
文章出处登录后可见!
