1. 共轭梯度算法介绍
共轭梯度(Conjugate Gradient)方法是一种迭代算法,可用于求解无约束的优化问题,例如能量最小化。常见的优化算法还有梯度下降法,相比于梯度下降法,共轭梯度法具有收敛更快,以及算法稳定性更好的优点。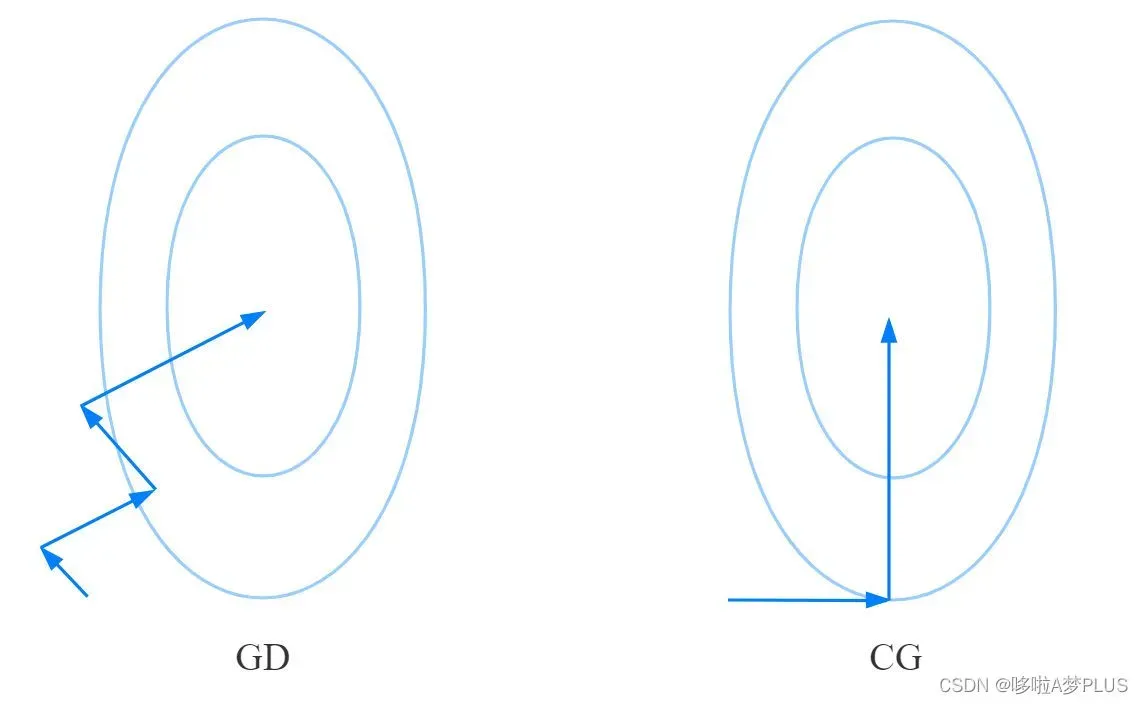
从上图可以看出来,梯度下降法优化过程中函数是沿着梯度的反方向逐步优化,后一步优化的结果会对前一步的优化结果造成影响,收敛较慢。而共轭梯度方法每一步的优化方向与前一步的优化方向是共轭的,因此并不会对前一步的优化结果造成影响,同时优化过程中保证在每一个方向上函数优化到最小值,从而保证沿着这些共轭方向优化完成后,函数能够达到全局最小值点。具体解释可以参考这篇文章:https://zhuanlan.zhihu.com/p/338838078
2. 实现共轭梯度法的两个重要组成部分
1.共轭方向的确定
共轭梯度法中新的共轭方向仅由上一步的梯度、新梯度和上一步的优化方向决定,即:
其中的定义方式有很多种,常用的有FR和PRP两种:
2.方向优化步长的确定
当优化方向确定之后,需要利用线性搜索技术确定优化的步长,即是寻找α>0使得
线搜索技术包含两大类,即精确线搜索技术和非精确线搜索技术,详见这篇文章:https://www.longzf.com/optimization/2/line_search/
精确线搜索技术包括牛顿法和二分法。由于以下代码中使用的线搜索技术是牛顿法,下面对牛顿法进行简单介绍。
牛顿法用于解决函数的最小值和最大值问题。函数的极值点应该有。将函数展开到二阶泰勒展开后,可以得到α的迭代公式:
note
由于数值计算过程中使用了差分法,这里简要列出一阶和二阶微分中使用的差分表达式:
其中是少量。
三、共轭梯度算法优化过程
- 计算初始梯度值
和优化方向
- 如果
,退出迭代过程,否则执行以下步骤
- 使用线性搜索算法(牛顿法)找到使
的步长 α,并更新
:
- 计算新梯度
- 根据前面提到的FR公式或PRP公式计算新的组合系数
- 计算新的共轭方向:
- 重复执行第2步
四、python实现共轭梯度算法
这里使用的测试函数的形式是:
可以看到函数存在最小值点(1, 1.5),以下是实现的python代码。
1.FR-CG
############共轭梯度算法#############
import numpy as np
import matplotlib.pyplot as plt
def testFun(x, y):
t = 3.0*x - 2.0*y
t1 = x - 1.0
z = np.power(t, 2) + np.power(t1, 4)
return z
def gradTestFun(x, y):
'''
求函数的梯度
'''
delta_x = 1e-6 #x方向差分小量
delta_y = 1e-6 #y方向差分小量
grad_x = (testFun(x+delta_x, y)-testFun(x-delta_x, y))/(2.0*delta_x)
grad_y = (testFun(x, y+delta_y)-testFun(x, y-delta_y))/(2.0*delta_y)
grad_xy = np.array([grad_x, grad_y])
return grad_xy
def getStepLengthByNewton(array_xy, array_d):
'''
采用牛顿法,精确线性搜索确定移动步长
'''
a0 = 1.0 #初始猜测值
e0 = 1e-6 #退出搜索循环的条件
delta_a = 1e-6 #对a作差分的小量
while(1):
new_a = array_xy + a0*array_d
new_a_l = array_xy + (a0-delta_a)*array_d
new_a_h = array_xy + (a0+delta_a)*array_d
diff_a0 = (testFun(new_a_h[0], new_a_h[1]) - testFun(new_a_l[0], new_a_l[1]))/(2.0*delta_a)
if np.abs(diff_a0) < e0:
break
ddiff_a0 = (testFun(new_a_h[0], new_a_h[1]) + testFun(new_a_l[0], new_a_l[1]) - 2.0*testFun(new_a[0], new_a[1]))/(delta_a*delta_a)
a0 = a0 - diff_a0/ddiff_a0
return a0
def plotResult(array_xy_history):
x = np.linspace(-1.0, 4.0, 100)
y = np.linspace(-4.0, 8.0, 100)
X, Y = np.meshgrid(x, y)
Z = testFun(X, Y)
plt.figure(dpi=300)
plt.xlim(-1.0, 4.0)
plt.ylim(-4.0, 8.0)
plt.xlabel("x")
plt.ylabel("y")
plt.contour(X, Y, Z, 40)
plt.plot(array_xy_history[:,0], array_xy_history[:,1], marker='.', ms=10)
xy_count = array_xy_history.shape[0]
for i in range(xy_count):
if i == xy_count-1:
break
dx = (array_xy_history[i+1][0] - array_xy_history[i][0])*0.6
dy = (array_xy_history[i+1][1] - array_xy_history[i][1])*0.6
plt.arrow(array_xy_history[i][0], array_xy_history[i][1], dx, dy, width=0.1)
def mainFRCG():
'''
使用CG算法优化,用FR公式计算组合系数
'''
ls_xy_history = [] #存储初始坐标的迭代结果
xy0 = np.array([4.0, -2.0]) #初始点
grad_xy = gradTestFun(xy0[0], xy0[1])
d = -1.0*grad_xy #初始搜索方向
e0 = 1e-6 #迭代退出条件
xy = xy0
while(1):
ls_xy_history.append(xy)
grad_xy = gradTestFun(xy[0], xy[1])
tag_reach = np.abs(grad_xy) < e0
if tag_reach.all():
break
step_length = getStepLengthByNewton(xy, d)
xy_new = xy + step_length*d
grad_xy_new = gradTestFun(xy_new[0], xy_new[1])
b = np.dot(grad_xy_new, grad_xy_new)/np.dot(grad_xy, grad_xy) #根据FR公式计算组合系数
d = b*d - grad_xy_new
xy = xy_new
array_xy_history = np.array(ls_xy_history)
plotResult(array_xy_history)
return array_xy_history
以下是运行结果
最终得到的最小值的坐标为[ 1.00113664, 1.50170496]
营业时间:
2.PRP-CG
换用PRP公式计算只需要将上面求解组合系数部分的代码作少量修改即可,代码为:
def mainPRPCG():
'''
使用CG算法优化,用PRP公式计算组合系数
'''
ls_xy_history = []
xy0 = np.array([4.0, -2.0])
grad_xy = gradTestFun(xy0[0], xy0[1])
d = -1.0*grad_xy
e0 = 1e-6
xy = xy0
while(1):
ls_xy_history.append(xy)
grad_xy = gradTestFun(xy[0], xy[1])
tag_reach = np.abs(grad_xy) < e0
if tag_reach.all():
break
step_length = getStepLengthByNewton(xy, d)
xy_new = xy + step_length*d
grad_xy_new = gradTestFun(xy_new[0], xy_new[1])
b = np.dot(grad_xy_new, (grad_xy_new - grad_xy))/np.dot(grad_xy, grad_xy) #根据PRP公式计算组合系数
d = b*d - grad_xy_new
xy = xy_new
array_xy_history = np.array(ls_xy_history)
plotResult(array_xy_history)
return array_xy_history
运行结果是:
得到的最小值的坐标是[ 1.00318321, 1.50477481]
营业时间:
3.GD
最后将梯度下降法的优化结果写在一起进行比较。以下是实现代码:
def mainGD():
'''
使用梯度下降法计优化函数
'''
ls_xy_history = []
xy0 = np.array([4.0, -2.0])
ls_xy_history.append(xy0)
grad_xy = gradTestFun(xy0[0], xy0[1])
alpha = 1e-3
e0 = 1e-3
xy = xy0
while(1):
tag_reach = np.abs(grad_xy)<e0
if tag_reach.all():
break
xy = xy - alpha*grad_xy
grad_xy = gradTestFun(xy[0], xy[1])
ls_xy_history.append(xy)
array_xy_history = np.array(ls_xy_history)
plotResult(array_xy_history)
return array_xy_history
运行结果是:
得到的最小值坐标是[ 0.9185095 , 1.37763925]
运行时是:
五、总结
对比可以发现,CG算法在计算的速度和准确度上都相较于GD算法有一定的优势。
文章出处登录后可见!
