概述

作为一种分类算法，生成方法朴素贝叶斯与判别方法思路是不一样的。简单地理解，朴素贝叶斯首先找到特征X和输出Y的联合概率 $P(X,Y)$ ，接着根据贝叶斯公式 $P(Y|X)=\frac{P(X,Y)}{P(X)}$ 求得预测类别。

贝叶斯方法的思想可以概括为：数据+先验概率=后验概率。后验概率是我们想要得到的概率分布。在此基础上，朴素贝叶斯有一个“朴素”的简单假设，即每个特征都是条件独立的，这是一个很强的假设，但在实际复杂场景中也能取得更好的效果。的结果。

由于我之前对这部分知识的理解还不够透彻，所以想尽可能详细地推导出朴素贝叶斯分类器的原理。为了更好的理解，我们先看一下全概率公式和贝叶斯公式的先验知识，最后给出朴素贝叶斯分类器的目标函数。

1. 总概率公式

假设事件 $Y_{1},Y_{2},...,Y_{K}$ 是样本空间中的一个完备事件组（即两对不相交，并集为完备集）， $P(Y_{k})> 0 (k=1,2,...,K)$ 。那么任何事件 $X$ 都可以根据 $Y_{k}$ 来划分，如下图所示：

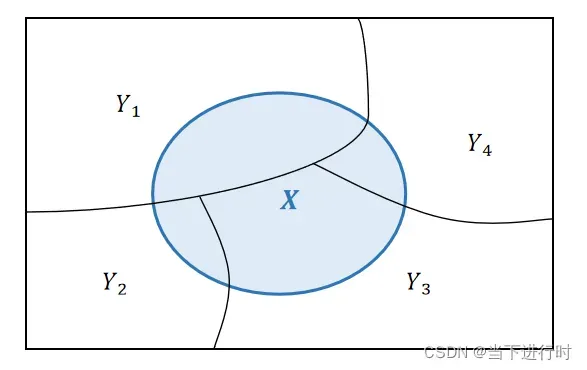
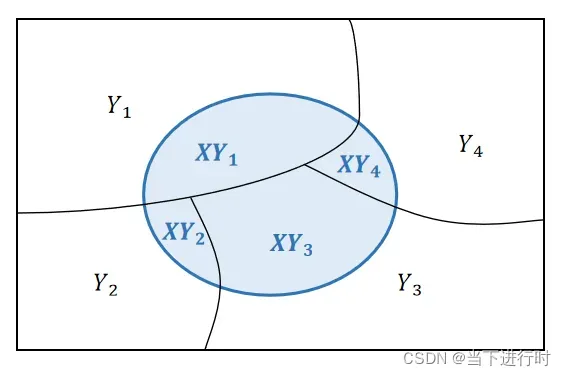
事件 $X$ 发生的概率表示为：

$P(X)=P(XY_{1})+P(XY_{2})+..+P(XY_{K})$

由条件概率公式可知

$P(XY_{1})=P(X)P(Y_{1}|X) =P(Y_{1})P(X|Y_{1})$

因此，事件 $X$ 发生的概率写为：

$P(X)=P(Y_{1})P(X|Y_{1})+P(Y_{2})P(X|Y_{2})+...+P(Y_{K})P(X|Y_{K})$

$=\sum_{k=1}^{K}P(Y_{k})P(X|Y_{k})$

↑ 这是总概率公式。

2.贝叶斯公式

贝叶斯公式是从条件概率和总概率推导出来的：

$P(Y_{k}|X)=\frac{P(XY_{k})}{P(X)}$

$=\frac{P(Y_{k})P(X|Y_{k})}{\sum_{k=1}^{K}P(Y_{k})P(X|Y_{k})}$

其中 $k=1,2,...,K$
$P(Y)$ 、 $P(X)$ 是先验概率（也称为边际概率），在计算中不考虑任何其他事件的影响。
$P(Y|X)$ 为后验概率，表示事件 $X$ 已经发生时事件 $X$ 发生的概率。

在分类任务中， $X$ 代表特征， $Y$ 代表类别标签，贝叶斯公式等价于：

3.朴素贝叶斯公式

在贝叶斯公式的基础上，如果加入一个很强的“朴素”假设，即特征的条件概率分布是独立的，则称为朴素贝叶斯。即朴素贝叶斯=贝叶斯定理+特征条件独立假设。

设输入空间，输出空间是所有的K类标记。定义在输入空间上的n维随机向量记作 $X$ ，定义在输出空间上的随机向量记作 $Y$ 。对于一个输入 $x$ 和它对应的输出 $y$ ，用下标代表样本，上标代表特征，贝叶斯公式中的条件概率分布写作：

$P(X=x|Y=c_{k})=P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)}|Y=c_{k}),$

$k=1,2,...,K$

在朴素贝叶斯中，特征独立性假设导致以下公式：

$P(X=x|Y=c_{k})=\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_{k})$

所以朴素贝叶斯将后验概率表示为：

$P(Y=c_{k}|X=x)=\frac{P(Y=c_{k})P(X=x|Y=c_{k})}{\sum_{k=1}^{K}P(Y=c_{k})P(X=x|Y=c_{k})}$

$=\frac{P(Y=c_{k})\prod_{j=1}^{n}P(X^{(i)}=x^{(i)}|Y=c_{k})}{\sum_{k=1}^{K}P(Y=c_{k})\prod_{j=1}^{n}P(X^{(i)}=x^{(i)}|Y=c_{k})}$

（说白了就是在贝叶斯公式的基础上，把独立的特征写成乘积的形式。）

4.朴素贝叶斯分类器

分类器输出后验概率最高的类，即：

$y=f(x)=arg\underset{c_{k}}{max}P(Y=c_{k}|X=x)$

$=arg\underset{c_{k}}{max}\frac{P(Y=c_{k})\prod_{j=1}^{n}P(X^{(i)}=x^{(i)}|Y=c_{k})}{\sum_{k=1}^{K}P(Y=c_{k})\prod_{j=1}^{n}P(X^{(i)}=x^{(i)}|Y=c_{k})}$

由于上式中的分母对于所有类都是相同的，所以朴素贝叶斯分类器的目标函数直接简化为分子：

$y=arg\underset{c_{k}}{max}P(Y=c_{k})\prod_{j=1}^{n}P(X^{(i)}=x^{(i)}|Y=c_{k})$

五、关于如何获取朴素贝叶斯的参数

在知道了朴素贝叶斯分类器的目标函数之后，就要考虑如何估计参数了。

目标函数涉及两个概率，一个是先验概率 $P(Y=c_{k})$ ，另一个是条件概率 $P(X^{(i)}=x^{(i)}|Y=c_{k})$ 。这两个概率是使用最大似然估计来估计的。

1、先验概率 $P(Y=c_{k})$ 的估计：

这个是最好计算的，不用考虑特征向量 $X$ ，直接统计训练集的标签就可以。设训练集共有N个样本，训练集表示为 $\left \{ {(x_{1},y_{1}),(x_{2},y_{2}),...},(x_{N},y_{N}) \right \}$ ，先验概率直接统计即可：

$P(Y=c_{k})=\frac{\sum_{i=1}^{N}I(y_{i}=c_{k})}{N}$

（式中 $I(\cdot )$ 为指示函数，括号为真时 $I=1$ 为真）。

2、条件概率 $P(X^{(i)}=x^{(i)}|Y=c_{k})$ 的估计：

由于特征有多个可能的取值，设第j个特征有 $S_{j}$ 个可能的取值 $\left \{ a_{j1},a_{j2},...,a_{jS_{j}} \right \}$ 。条件概率的估计为：

$P(X^{(j)}=a_{jl}|Y=c_{k})=\frac{\sum_{i=1}^{N}I(x_{i}^{(j)}=a_{jl},y_{i}=c_{k})}{\sum_{i=1}^{N}I(y_{i}=c_{k})}$

（类似地，其中 $I(\cdot )$ 是指示函数）。

在获得两个概率的最大似然估计后，使用朴素贝叶斯分类器的目标函数进行预测。

参考：

李航《统计学习方法（第2版）》

文章出处登录后可见！

已经登录？立即刷新

监督学习：朴素贝叶斯

概述

1. 总概率公式

2.贝叶斯公式

3.朴素贝叶斯公式

4.朴素贝叶斯分类器

五、关于如何获取朴素贝叶斯的参数

相关推荐