作者‖ Cocoon
编辑‖3D视觉开发者社区
✨如果觉得文章内容不错，别忘了支持三遍😘~
介绍：
本文由英特尔中国提出，发表于ICLR 2017，本文提出了一种渐进式量化的方法——INQ （被引：797），通过先分组量化，冻结已量化的部分并训练未量化的部分，重复上述步骤直到所有权重都完成量化。这种方法可以把一个预训练的全精度模型近乎无损地压缩成一个低精度的模型，在Alexnet，VGG，ResNet等模型上都表现良好，精确度有较大提升。
论文链接：https://arxiv.org/pdf/1702.03044v2.pdf
代码链接：https://github.com/Zhouaojun/IncrementalNetwork-Quantization
概述
该方法发表于ICLR 2017，由英特尔中国提出，目的是希望能够无损地用低位宽的权重表达神经网络，是量化领域中的经典论文之一。具体地，文章提出了一种渐进量化方式，其主要包含三个相互依赖的操作：权重划分、分组量化与重训练。即，首先通过某种分组规则将权重分为两个互不相干的组，然后对其中一组进行量化，而后将其冻结，再对另外一组以渐进迭代的方式进行重训练，目的是补偿第一组的量化损失。其中，渐进迭代的终止条件是所有的权值都被量化完毕。
下文将对权值量化的方式、渐进量化的策略以及整体的算法步骤进行介绍，并在实验部分贴出INQ相比起其他SOTA的对比效果及部分消融实验结果。
渐进式量化
变长编码的权重量化（variable-length encoding scheme）
姓名：
假设预训练的全精度的模型为，其中
表示第
层的权重，
表示在模型中要学习参数的层数。为了对接下来的表达进行简化，我们只考虑对卷积层和全连接层进行量化。举个例子，就像
、
、
以及
之类的网络而言，对应于其中的卷积层，
可以是4D的tensor，对应于其中的全连接层，
可以是2D的矩阵。
设低位版本的权重为，其中的每个元素只能从以下集合中选择：
(1)
其中和
是两个整数，
。
也就是说，量化后的权重数值范围由和
决定，在一定范围以外的数值会被直接怼成0。
任务详情：
给定一个预训练的全精度模型，INQ的目的是在尽可能不损失精度的前提下，将该32位的浮点型权重变换到2的整数幂或0上。
此外，希望能够在网络无损量化的约束下，探索能够支持的最极端的小位宽。
怎么做？
在INQ中，期待的位宽需要我们预先确定好，然后我们只要确定好超参
就可以了，因为
可以根据位宽
以及超参
推断而得。
的计算方法是一个经验有点复杂但实践证明有用的公式：
(2)
其中，计算为：
(3)
其中，计算为：
(4)
其中，是逐个元素的操作。
当得到时，通过
自然可以得到
，例如当
、
、
时。
当候选池确定后，我们进一步将
中的每个元素通过以下公式转化为低位量化值：
其中，和
是在侯选池
中相邻的两个元素，进而迫使量化后的权重都能够是侯选池中的元素。这里有一个小细节，即在公式（2）中的系数
的设定与公式（4）是强呼应的。
假设我们希望模型量化位数是5，由于0不能够用2的整数次幂来表达，因此我们额外给出一个比特来表示0值，剩下的4个比特则用来表达最多16个2的整数次幂数。换句话说，候选的量化值的个数最多只有
个，这也对应点了该小节的“变长（variable-length ）”的题。
显然，上述量化方法是线性的，另一种选择是“对数”。尽管这种替代方案可能是有效的，但它在实现和计算开销方面存在更大的困难。 .
渐进式量化策略
认为：
虽然我们可以直接用上面的量化方法直接量化全精度模型，但难免会遇到很大的精度损失。
在当时已有的量化工作中，比如说HashedNet（Chen 等， 2015），BinaryConnect（Courbariaux等，2015）等，其实大家都会面临着掉点的问题，在大型的数据面前，掉点问题会显得更加突出。然而，发现已有的量化工作有一个共性，就是在量化的过程中都采用了全局的策略，即所有的权重参数同时地转换为低比特位的量化参数。而INQ认为，这种全局策略是导致精度损失的原因之一。此外，当量化比特位越低时，精度损失的越厉害。
INQ受当时的某些剪枝工作的启发，即在剪枝中，移除某些不那么重要的神经网络中的层所带来的精度损失往往可以通过后续的训练弥补回来，因此，INQ做出了这样的推测：改变网络权重的重要性是获得无损量化的关键。
战略：
在上述假设的基础上，INQ提出了三个互相依赖的操作：权重划分、逐组的量化、重训练。
权重划分将全精度的CNN中的每一层的权重划分为两个互不相关的组，这两个组主要起着互补的作用。在第一组的权重主要用于构成全精度网络的低比特版本，因此其中的权重直接使用公式（4）进行量化，而第二组的权重，则用于补偿模型精度的损失，因此他们需要被重训练。
一旦第一次量化和再训练操作结束，这三个操作将在第二组权重中以迭代的方式进行。迭代结束的条件是所有权重都已量化。这个过程称为渐进式网络量化和精度提高的过程。该过程的优点是低比特量化精度的损失可以通过渐进策略很好地补偿。
INQ迭代的过程如Fig 2所示：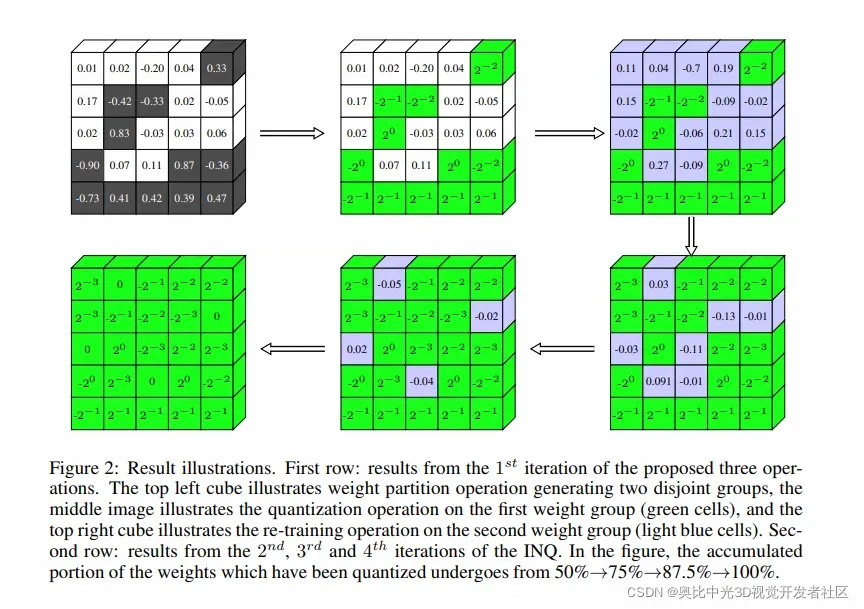
在Fig 2中，第一行表示在提出的三个操作中的第一次迭代，最左上角的cube表示权重划分操作，该操作产生了两个互不相关的组，中间的影像则表示对第一组权重的量化操作（绿色表示），第一行最右边表示对第二组的权重（浅蓝色表示）进行重训练。第二行表示了INQ中第二次、第三次、第四次的迭代。在这样的过程中，慢慢地量化参数的比例为50% – 75% – 87.5% – 100%。
对于层，权重划分可以表示为：
其中，代表第一组需要量化的权重参数，
代表第二组需要重新训练的参数。具体的分组标准留给实验部分作进一步说明。
这里定义了一个二进制矩阵来帮助区分上述两种类型的权重。即
表示
，
表示
。
渐进式网络量化算法
本节主要介绍训练方法。
仍以层为例，量化优化问题可表示为：
其中，代表网络损失，
是正则项，
是正系数，所有权重只能从候选池中选择。直接求解这样的优化公式具有挑战性，而且容易遇到不收敛的问题。
而前面我们提到过所谓的权重划分以及逐组量化，这两个操作可以使得公式（6）进一步变化到以下形式：
由于和
已知，优化公式直接用
等优化算法求解。也就是说，再训练时的权重更新方式为：
其中代表正学习率。注意二进制矩阵
的存在会导致只有浮点数被更新，这类似于一些剪枝方法，只有没有被移除的层才会被重新训练。
INQ的所有流程描述在以下算法中：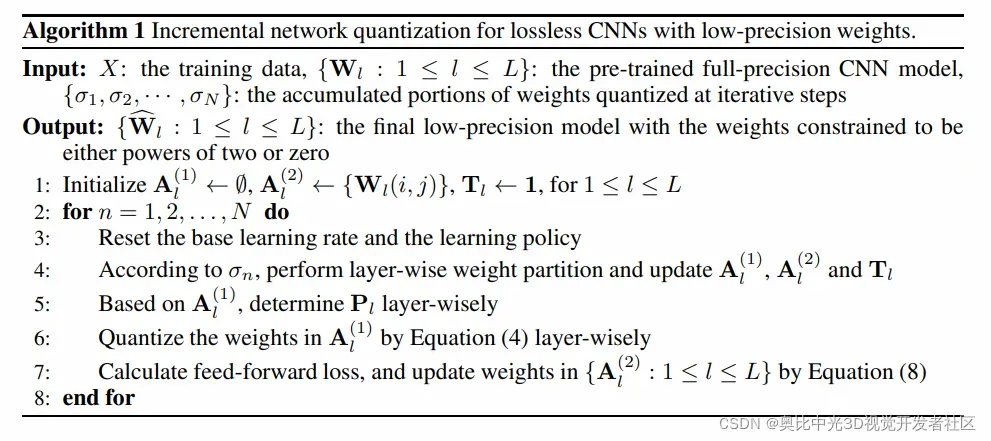
实验
ImageNet 上的结果
下表为将全精度不同的CNN模型通过INQ的方式转换为5比特模型时的掉点情况：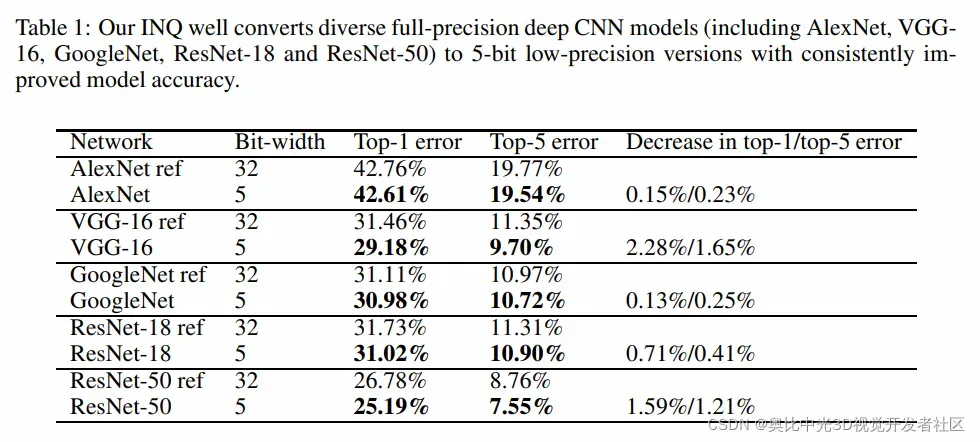
权重分组策略
权重分组将直接影响后续的分组量化和再训练操作。有两种候选的分组策略。一种是受到剪枝算法的启发，认为绝对值越大的权重相对更重要，另一种是随机划分。
本节对ResNet进行量化，下表总结了INQ使用不同分组策略时5位量化的对比结果，显然，使用由剪枝算法启发的分组策略效果相对于随机划分要好：
也因此，文章采用了“Pruning-inspired”，即由剪枝算法启发的权值分组策略。
不过，文章也指出了如何划分权重作为后续值得探讨的问题之一。
期望位宽与模型精度之间的trade-off
与章节中3.2的实验设定一样，本节逐渐的减少量化位数（对应地增加迭代次数），观察无损量化的位宽极限。
具体有：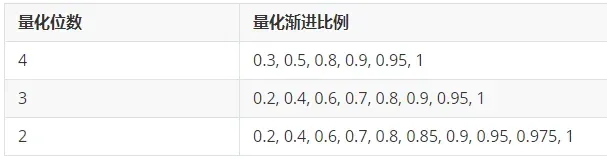
实验结果是：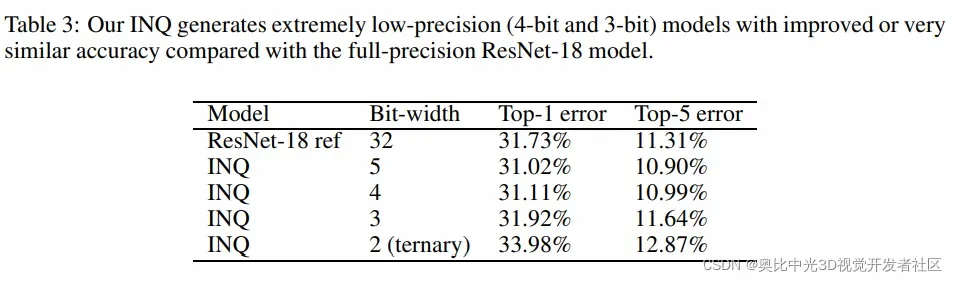
尽管看起来量化到2比特的时候，掉点比较厉害，但是相对于当时的SOTA来说，已经有所提升，具体对比结果见下表：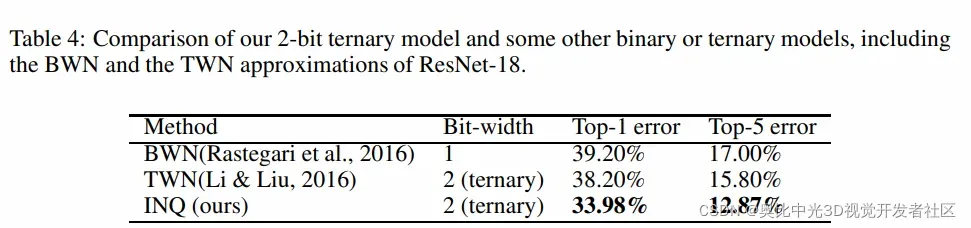
低位压缩
在模型压缩角度上，实验与其他模型压缩的方式进行了对比实验，实验表明INQ在5位或4位的量化上几乎没有损失，且相比起其他压缩的方式，比如说剪枝(Han等, 2015)、矢量量化（vector quantization）(Gong等, 2014)、深度压缩(Han等, 2016)等，INQ的最终权值是2的整数次幂或0，其显著优势在于可以用于FPGA等硬件上。
具体实验结果如下表所示：
综上所述
本文对经典量化方法之一：渐进量化，进行了介绍。该方法依赖三个核心操作：权重分组、分组量化、重训练，对全精度的神经网络模型进行预设位宽的量化。该方法相比起之前的量化方法最大的不同在于并非将所有权重同时进行量化，而是采用了渐进的策略，逐渐地对模型进行量化，与其他SOTA的对比实验结果表现了该策略的优越性。特别地，文章还在实验部分探索了无损量化的极限位宽，结果表明，尽管在两比特（3值）量化的掉点比较严重，却还是相对于当时其他的SOTA要好一些。
参考
- Matthieu Courbariaux, Bengio Yoshua, and David Jean-Pierre. Binaryconnect: Training deep neural networks with binary weights during propagations. In NIPS, 2015.
- Song Han, Jeff Pool, John Tran, and William J. Dally. Learning both weights and connections for efficient neural networks. In NIPS, 2015.
- Song Han, Jeff Pool, John Tran, and William J. Dally. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. In ICLR, 2016.
- Wenlin Chen, James T. Wilson, Stephen Tyree, Kilian Q. Weinberger, and Yixin Chen. Compressing neural networks with the hashing trick. In ICML, 2015.
- Yunchao Gong, Liu Liu, Ming Yang, and Lubomir Bourdev. Compressing deep concolutional networks using vector quantization. arXiv preprint arXiv:1412.6115v1, 2014.
版权声明：本文为奥比中光3D视觉开发者社区特约作者授权原创发布，未经授权不得转载，本文仅做学术分享，版权归原作者所有，若涉及侵权内容请联系删文。
3D视觉开发者社区是由奥比中光给所有开发者打造的分享与交流平台，旨在将3D视觉技术开放给开发者。平台为开发者提供3D视觉领域免费课程、奥比中光独家资源与专业技术支持。点击加入3D视觉开发者社区，和开发者们一起讨论分享吧~
也可移步微信关注官方公众号 3D视觉开发者社区 ，获取更多干货知识哦。
文章出处登录后可见！
