一、简介

本文前半部分算法实现参考的为姚健康老师的论文，这篇论文在万方学术平台可以免费下载：http://d.g.wanfangdata.com.cn/Periodical_jxkx200701002.aspx

后半部分算法涉及到稀疏优化，我在之前的博客中介绍了实现原理并给出了代码，链接如下：稀疏优化L1范数最小化问题求解之基追踪准则(Basis Pursuit)——原理及其Python实现

2. 问题的重述

给定一个超定线性方程组：

其中，找到，这样

即求超定线性方程组在范数意义下的解，简称范数极小化问题1。

定义：设为问题的解，称为问题的最小模残差向量。如果能够得到最小的-模残差向量，则一致线性方程组的解就是问题的解。

2.求最小模残差向量的性质和方法

依据文献2中的说明，我们得到如下定理：

定理：设有 2 个超定线性方程组，若存在可逆阵，使，则这 2 个超定线性方程组的极小模剩余向量相同。

令（为阶可逆矩阵），则方程可转化为公式：

假设方程组的最小模残差向量为，则由上式和方程组具有相同的最小模残差向量，所以也是式的最小模残差向量，记为，所以

如果我们订购

那么最小模残差向量满足以下线性方程：

在

具体转换过程可以参考姚老师的论文。因此，需要最小的模残差向量，即需要满足公式的，使得最小。

3.一种基于基追踪准则的求解算法

从方程式。 ，原超定线性方程组的最小模残差向量可以通过以下约束不可微优化问题得到：

表示问题的最优解，方程组是原方程的一致线性方程组，其解是问题的解：

在问题中，如果我们定义：

那么问题变成如下问题：

对于极小模剩余向量，考虑到我们的求解应当尽可能逼近精确解，即极小模剩余向量中的元素应当尽可能为0。这样问题的形式又回到了范数最小化问题中的稀疏优化问题。

参考我的这篇博客求解上述稀疏优化问题：稀疏优化L1范数最小化问题求解之基追踪准则(Basis Pursuit)——原理及其Python实现

四、超定线性方程组极小范数求解Python代码

采用 Python 中scipy模块内置的linprog函数求解线性方程组，编写代码如下：

import numpy as np 
from scipy import optimize as op

def OLE_linprog(A, b):
    '''
    Ax = b (Given A & b, try to derive x)
    
    Parameters
    ----------
    A : matrix like.
    b : array like.

    Returns
    -------
    x : array
        Minimal L1 norm solution of the system of equations.
        
    Reference
    ---------
    YAO Jian-kang. An Algorithm for Minimizing l1-Norm to Overdetermined Linear Eguations[J]. 
    JIANGXI SCE7NICE, 2007, 25(1): 1-4.(Available at: 
    http://d.g.wanfangdata.com.cn/Periodical_jxkx200701002.aspx)
        
    Version: 1.0 writen by z.q.feng @2022.03.13
    '''
    A, b = np.array(A), np.array(b)
    if np.size(A, 0) < np.size(A, 1):
        raise ValueError('Matrix A rows must greater than columns!')
    m, n = A.shape
    # Trans A into two matrix(n x n and (m - n) x n)
    A1, A2 = A[:n, :], A[n:, :]
    if np.linalg.matrix_rank(A) >= n:
        # inverse of A1 
        A1_ = np.linalg.inv(A1)
    else:
        # Generalized inverse of A1 
        A1_ = np.linalg.pinv(A1)
    # c_ij = A2 * A1_
    c = np.dot(A2, A1_)
    # r(n+1:m) = A2*inv(A1)*r(1:n) + d
    d = np.dot(c, b[:n]) - b[n:]
    # Basic-Pursuit, target function = sum(u, v)
    t = np.ones([2 * m, 1])
    # Aeq_ = [c I(m-n)]
    Aeq_ = np.hstack([-c, np.eye(m - n, m - n)])
    # Aeq[u v] = Aeq_ * (u - v)
    Aeq = np.hstack([Aeq_, -Aeq_])
    # u, v > 0
    bounds = [(0, None) for i in range(2 * m)]
    # r0 = [u; v]
    r0 = op.linprog(t, A_eq = Aeq, b_eq = d, bounds = bounds,
                    method='revised simplex')['x']
    # Minimal L1-norm residual vector, r = u - v
    r = np.array([r0[:m] - r0[m:]])
    # Solving compatible linear equations Ax = b + r
    # Generalized inverse solution
    x = np.linalg.pinv(A).dot(b + r.T)
    return x

采用 MATLAB 求解的由于篇幅问题我就不放了，私信我。

五、检验检测

1. 矩阵A满秩情况

对于线性方程，通过生成给定的和，并制作，我们可以认为是问题的最优解。然后我们用上面的函数求解得到它的经验解，用定义它的恢复残差，用plot来确定解的精度。

if __name__ == '__main__':
    m, n = 256, 128
    # 256x128矩阵，每个元素服从Gauss随机分布
    A = np.random.randn(m, n)
    # 128x1矩阵，每个元素服从Gauss随机分布
    # b = A * u, 则 Au - b = 0，u 即为我们要求的精确解
    u = np.random.randn(n, 1)
    b = np.dot(A, u)
    alpha = OLE_linprog(A, b)
    # 恢复残差 
    print('\n恢复残差：', np.linalg.norm(alpha - u, 2))
    # 绘图
    plt.figure(figsize = (8, 6))
    # 绘制原信号
    plt.plot(u, 'r', linewidth = 2, label = 'Original')
    # 绘制恢复信号
    plt.plot(alpha, 'b--', linewidth = 2, label = 'Recovery')
    plt.grid() 
    plt.legend()
    plt.show()

得到恢复残差为6.0407e-14，恢复信号图如图所示(信号随机生成，每次结果均不一样)。

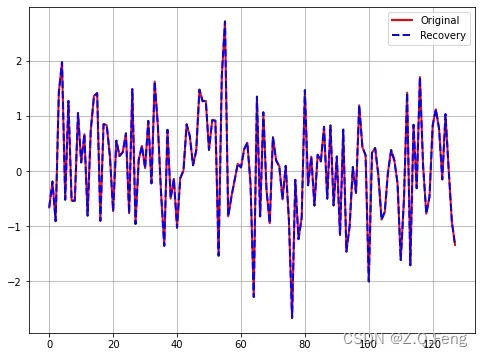
2. 矩阵A列缺秩情况

根据式可以看出，若矩阵行不满秩，即，我们的方法是不需要做对应改变的，而若矩阵列缺秩，则需要使用矩阵的Moore-Penrose逆矩阵替代在式中构造。

下面我们通过代码让矩阵列秩亏缺1：

A(:, n) = zeros(m, 1);

运行代码，得到恢复残差为0.2551，恢复信号图如图所示(信号随机生成，每次结果均不一样)。可以看到，虽然误差增大了，但是还在允许范围内。

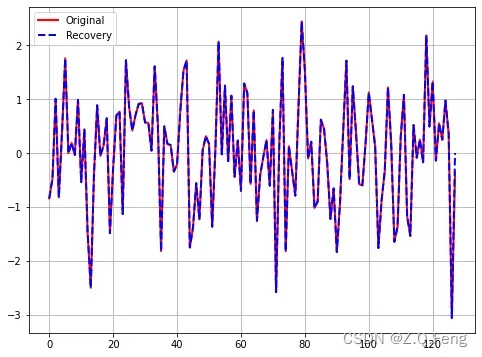
6.总结

目前解决问题的方法很多，主要有：

• 线性规划方法；
  
• 投影下降法；
  
• 有效的设置方法；
  
• 区间法等
  

上述方法各有优缺点。比如线性规划法增加尺度，投影下降算法太复杂难以被工程技术人员掌握，有效集法比其他方法更直观，算法简单，区间法太复杂，并且没有最优解区间。检查难度更大。本文利用最小的模残差向量将问题转化为有约束的不可微优化问题，进而求解出一致的线性方程组。该算法具有不扩大规模、简单易操作的优点。