内容

1 K的选择

1.1 肘部法则(Elbow method)

1.2 目标法则

1.3 间隔统计量 Gap Statistic

1.4 关于K值选择的改进算法——ISODATA算法

2 聚类算法的评估

2.1 估计聚类趋势

2.2 判定数据簇数

2.3 测定聚类质量

2.3.1 轮廓系数（Silhouette Coefficient）

2.3.2 均方根标准偏差（Root-mean-square standard deviation，RMSSTD）

2.3.3 R方（R-Square）

2.3.4 改进的HubertΓ统计

1 K的选择

没有所谓最好的选择聚类数的方法，通常是需要根据不同的问题，人工进行选择的。选择的时候思考我们运用 K-均值算法聚类的动机是什么，然后选择能最好服务于该目标的聚类数。

1.1肘部法则(Elbow method)

改变聚类数K，然后进行聚类，计算损失函数，拐点处即为推荐的聚类数(即通过此点后，聚类数的增大也不会对损失函数的下降带来很大的影响，所以会选择拐点)

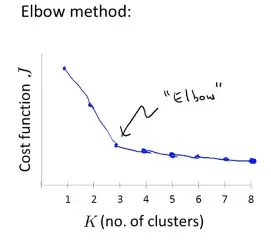
由图可见，K值越大，距离和越小；并且，当K=3时，存在一个拐点，就像人的肘部一样；当K (1,3)时，曲线急速下降；当K>3时，曲线趋于平稳。手肘法认为拐点就是K的最佳值。

但是也有损失函数随着K的增大平缓下降的例子，此时通过肘部法则选择K的值就不是一个很有效的方法了(下图中的拐点不明显，k=3,4,5有类似的功能) 。

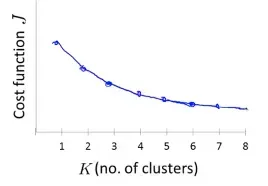
肘部法是一种经验方法，缺点是不够自动化。

1.2目标法则

通常K均值聚类是为下一步操作做准备，例如：市场分割，社交网络分析，网络集群优化，下一步的操作都能给你一些评价指标，那么决定聚类的数量更好的方式是：看哪个聚类数量能更好的应用于后续目的。

例如对于T恤衫的尺码进行聚类的方法，如左图将其聚为3类(S,M,L)，右图将其聚为5类(XS,S,M,L,XL)进行表示，这两种聚类都是可行的，我们可以根据聚类后用户的满意程度或者是市场的销售额来决定最终的聚类数量。

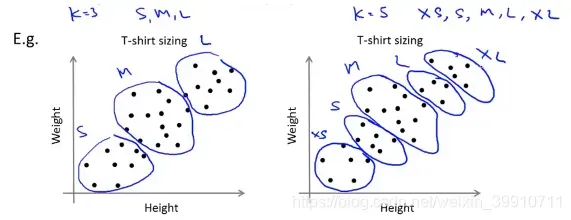
1.3 间隔统计量 Gap Statistic

Gap Statistic方法的优点是，不再需要肉眼判断，而只需要找到最大的Gap statistic所对应的K即可，因此该方法也适用于批量化作业。在这里我们继续使用上面的损失函数，当分为K簇时，对应的损失函数记为Dk。Gap Statistic定义为：

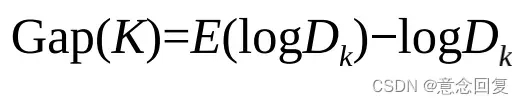
其中E(logDk)是logDk的期望，一般通过蒙特卡洛模拟产生。我们在样本所在的区域内按照均匀分布随机地产生和原始样本数一样多的随机样本，并对这个随机样本做K-Means，从而得到一个Dk。如此往复多次，通常20次，我们可以得到20个logDk。对这20个数值求平均值，就得到了E(logDk)的近似值。那么Gap(K)有什么物理含义呢？它可以视为随机样本的损失与实际样本的损失之差。试想实际样本对应的最佳簇数为K，那么实际样本的损失应该相对较小，随机样本损失与实际样本损失之差也相应地达到最大值，从而Gap(K)取得最大值所对应的K值就是最佳的簇数。

1.4 关于K值选择的改进算法——ISODATA算法

当K值的大小不确定时，可以使用ISODATA算法。ISODATA的全称是迭代自组织数据分析法。在K均值算法中，聚类个数K的值需要预先人为地确定，并且在整个算法过程中无法更改。而当遇到高维度、海量的数据集时，人们往往很难准确地估计出K的大小。ISODATA算法就是针对这个问题进行了改进，它的思想也很直观。当属于某个类别的样本数过少时，把该类别去除；当属于某个类别的样本数过多、分散程度较大时，把该类别分为两个子类别。ISODATA算法在K均值算法的基础之上增加了两个操作，一是分裂操作，对应着增加聚类中心数；二是合并操作，对应着减少聚类中心数。ISODATA算法是一个比较常见的算法，其缺点是需要指定的参数比较多，不仅仅需要一个参考的聚类数量Ko，还需要制定3个阈值。下面介绍ISODATA算法的各个输入参数。

（1）预期的聚类中心数目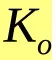。在ISODATA运行过程中聚类中心数可以变化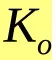，是一个用户指定的参考值，该算法的聚类中心数目变动范围也由其决定。具体地，最终输出的聚类中心数目常见范围是从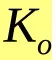的一半，到两倍。

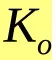（2）每个类所要求的最少样本数目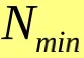。如果分裂后会导致某个子类别所包含样本数目小于该阈值，就不会对该类别进行分裂操作。

（3）最大方差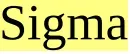。用于控制某个类别中样本的分散程度。当样本的分散程度超过这个阈值时，且分裂后满足（1），进行分裂操作。

（4）两个聚类中心之间所允许最小距离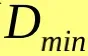。如果两个类靠得非常近（即这两个类别对应聚类中心之间的距离非常小），小于该阈值时，则对这两个类进行合并操作。

如果希望样本不划分到单一的类中，可以使用模糊C均值或者高斯混合模型。

2 聚类算法的评估

人的归纳思维能力强，善于从大量零散的事实或数据中找出一般规律，得出合乎逻辑的结论。以用户观看视频的行为为例，有很多直观的总结方式。比如，从观看内容来看，可以分为漫画、偶像剧、科幻电影等；从常用设备来看，可分为台式电脑、手机、平板便携设备、电视等；从使用时间上看，有用户在晚上、中午、每天观看、仅在周末观看等等。所有用户的有效分组对于理解用户并向他们推荐适当的内容很重要。通常这类问题不具备观测数据的标签或分组信息，需要通过算法模型寻找数据的内在结构和模式。

数据的聚类取决于实际需要，也取决于数据的特征度量和评估数据相似性的方法。与监督学习相比，无监督学习通常没有标注数据，模型和算法的设计直接影响最终输出和模型的性能。为了评估不同聚类算法的性能，我们需要了解常见数据聚类的特征。

由中心定义的数据簇：这类数据集往往呈球形分布，通常将中心定义为质心，即该数据簇中所有点的平均值。集合中的数据比其他集群的中心更靠近中心。
由密度定义的数据集群：这种类型的数据集表现出与周围数据集群显着不同的密度，无论是密集的还是稀疏的。当数据集群不规则或相互缠绕，带有噪声和异常值时，通常使用基于密度的集群定义。
连通性定义的数据簇：该类数据集中的数据点与数据点之间存在连接关系，整个数据簇表示为一个图结构。该定义适用于不规则形状或纠缠的数据簇。
概念上定义的数据集群：这类数据集中的所有数据点都有一些共同的属性。

由于数据以及需求的多样性，没有一种算法能够适用于所有的数据类型、数据簇或应用场景，似乎每种情况都可能需要一种不同的评估方法或度量标准。例如，K均值聚类可以用误差平方和来评估，但是基于密度的数据簇可能不是球形，误差平方和则会失效。在许多情况下，判断聚类算法结果的好坏强烈依赖于主观解释。尽管如此，聚类算法的评估还是必需的，它是聚类分析中十分重要的部分之一。

聚类评估的任务是估计在数据集上聚类的可行性，以及聚类方法产生的结果的质量。这个过程进一步分为三个子任务。

2.1 估计聚类趋势

这一步骤是检测数据分布中是否存在非随机的簇结构。如果数据是基本随机的，那么聚类的结果也是毫无意义的。我们可以观察聚类误差是否随聚类类别数量的增加而单调变化，如果数据是基本随机的，即不存在非随机簇结构，那么聚类误差随聚类类别数量增加而变化的幅度应该较不显著，并且也找不到一个合适的K对应数据的真实簇数。

另外，我们也可以应用霍普金斯统计量（Hopkins Statistic）来判断数据在空间上的随机性。首先，从所有样本中随机找n个点，记为，对其中的每一个点，都在样本空间中找到一个离它最近的点并计算它们之间的距离，从而得到距离向量；然后，从样本的可能取值范围内随机生成n个点，记为，对每个随机生成的点，找到一个离它最近的样本点并计算它们之间的距离，得到（的计算方式是另外生成一个均匀分布，从这个分布里采样数据，计算与数据集D中数据点的最近距离得到）。霍普金斯统计量H可以表示为

如果样本接近随机分布，那么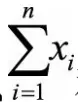和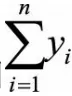的取值应该比较接近，即H的值接近于0.5（如果D也是一个均匀分布的话，那么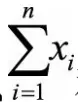和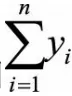就会很接近,H就会接近0.5）；如果聚类趋势明显，则随机生成的样本点距离应该远大于实际样本点的距离，即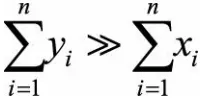，H的值接近于1（D中的数据不是均匀分布的，那么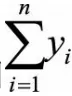就会大于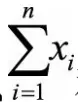，H就会大于0.5，就有可能存在簇）。

2.2 判定数据簇数

确定聚类趋势之后，我们需要找到与真实数据分布最为吻合的簇数，据此判定聚类结果的质量。数据簇数的判定方法有很多，例如手肘法和Gap Statistic方法。需要说明的是，用于评估的最佳数据簇数可能与程序输出的簇数是不同的。例如，有些聚类算法可以自动地确定数据的簇数，但可能与我们通过其他方法确定的最优数据簇数有所差别。

2.3 测定聚类质量

给定预设的聚类数量，不同的聚类算法会输出不同的结果。如何确定哪个聚类结果质量更高？在无监督的情况下，我们可以通过检查集群的分离程度和集群的紧凑程度来评估集群的效果。定义评估指标可以展示受访者实际解决和分析问题的能力。其实测量指标可以有很多种，下面列出几种常用的测量指标。

2.3.1 轮廓系数（Silhouette Coefficient）

Silhouette method 会衡量对象和所属簇之间的相似度——即内聚性（cohesion）。当把它与其他簇做比较，就称为分离性（separation）。该对比通过 silhouette 值来实现，后者在 [-1, 1] 范围内。Silhouette 值接近 1，说明对象与所属簇之间有密切联系；反之则接近 -1。若某模型中的一个数据簇，生成的基本是比较高的 silhouette 值，说明该模型是合适、可接受的。

方法：

1）计算样本i到同簇其他样本的平均距离a(i)。a(i)越小，说明样本i 越应该被聚类到该簇。将a(i)称为样本i 的簇内不相似度。簇C中所有样本的a(i)均值称为簇C的簇不相似度。

2）计算样本i到其他某簇C(j)的所有样本的平均距离b(ij)，称为样本i与簇C(j)的不相似度。定义为样本i的簇间不相似度：b(i) =min{bi1, bi2, …, bik}，b(i)越大，说明样本i越不属于其他簇。

3）根据样本 i 的簇内不相似度a i 和簇间不相似度b i ，定义样本 i 的轮廓系数：

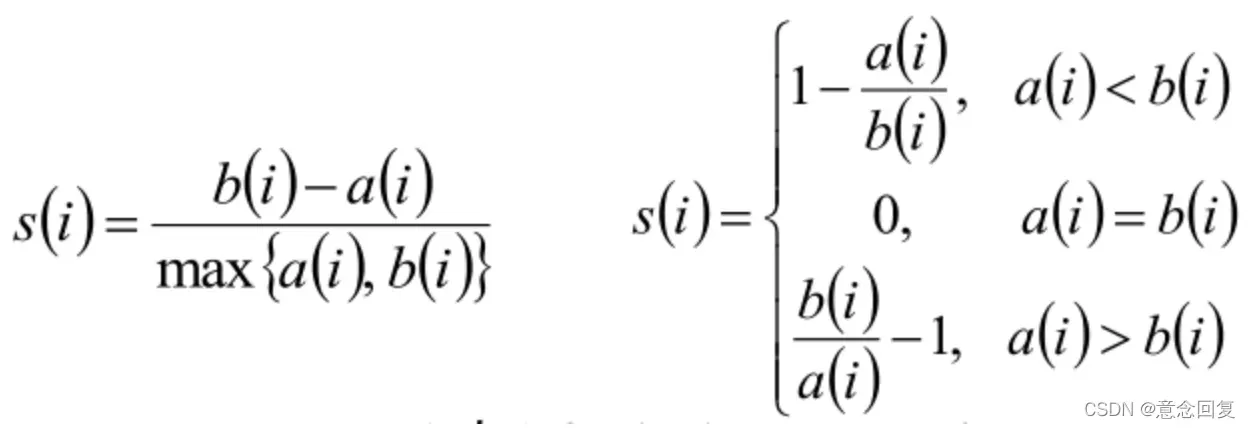
4）判断：

s(i)接近1，则说明样本i聚类合理
s(i)接近-1，则说明样本i更应该分类到另外的簇
若s(i) 近似为0，则说明样本i在两个簇的边界上

a(i)反映的是i所属簇中数据的紧凑程度，b(i)反映的是该簇与其他临近簇的分离程度。显然，b(i)越大，a(i)越小，对应的聚类质量越好。

所有样本的s(i )的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。但是，其缺陷是计算复杂度为O(n^2)，需要计算距离矩阵，那么当数据量上到百万，甚至千万级别时，计算开销会非常巨大。

2.3.2 均方根标准偏差（Root-mean-square standard deviation，RMSSTD）

用于衡量聚合结果的同质性，即紧凑程度，定义为：

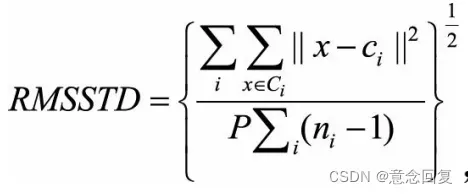
其中Ci代表第i个簇，ci是该簇的中心，x∈Ci代表属于第i个簇的一个样本点，ni为第i个簇的样本数量，P为样本点对应的向量维数。可以看出，分母对点的维度P做了惩罚，维度越高，则整体的平方距离度量值越大。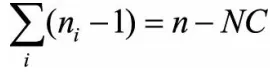，其中n为样本点的总数，NC为聚类簇的个数，通常NC<的值接近点的总数，为一个常数。综上，RMSSTD可以看作是经过归一化的标准差。

2.3.3 R方（R-Square）

它可以用来衡量聚类的差异程度，定义为

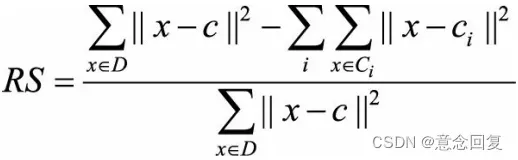
其中D代表整个数据集，c代表数据集D的中心点，从而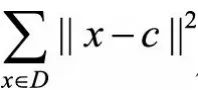代表将数据集D看作单一簇时的平方误差和。与上一指标RMSSTD中的定义相同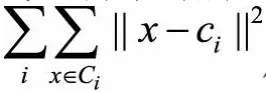，代表将数据集聚类之后的平方误差和，所以RS代表了聚类之后的结果与聚类之前相比，对应的平方误差和指标的改进幅度。

2.3.4 改进的HubertΓ统计

通过数据对的不一致来评估集群中的差异，定义为

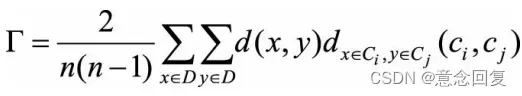
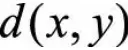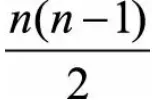其中表示点x到点y之间的距离，代表点x所在的簇中心与点y所在的簇中心cj之间的距离，为所有(x,y)点对的个数，因此指标相当于对每个点对的和做了归一化处理。理想情况下，对于每个点对(x,y)，如果d(x,y)越小，对应的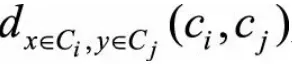也应该越小（特别地，当它们属于同一个聚类簇时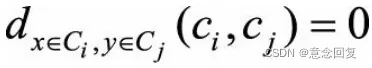，）；当d(x,y)越大时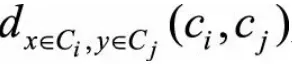，的取值也应当越大，所以Γ值越大说明聚类的结果与样本的原始距离越吻合，也就是聚类质量越高。