Momentum
是梯度校正
SGB的缺点:
其更新方向完全依赖于当前batch,因而其更新十分不稳定
例如:Data数据分成三个批次batch1,batch2,batch3,在使用梯度下降的过程中,batch1可能求得的梯度是5,batch2求得的梯度是-3,batch3求得的梯度是5,那么loss在沿着batch1方向下降后,batch2又会沿着相反的方向回去。这就导致了梯度下降的不稳定性。
解决:
momentum动量模仿的是物体的惯性,在更新的时候一定程度上保留了之前的更新的方向。
过程是附加过程。因此,您可以在提高稳定性的同时更快地学习。有一定的摆脱局部最优解的能力。
公式:
SGD公式:
momentum动量公式将原来的部分改成了
即表示
是累积的范围和每次调整的范围。
……
当是0的时候,由公式可以看出那就是SGD。一开始梯度比较大这个超参可以小一点0例如0.5,当梯度比较小的时候,可以改大一点例如0.9。
Momentum用的比较多,纯的SGD在深度学习里面用的比较少。
# 实现动量的梯度下降算法
opt = tf.keras.optimizers.SGD(learning_rate=0.1, momentum=0.9)
# 定义要更新的参数
var = tf.Variable(1.0)
var0 = var.value()
# 定义损失函数
loss = lambda :(var**2)/2.0
# 第一次更新
opt.minimize(loss, [var])
var1 = var.value()
# 第二次更新
opt.minimize(loss, [var])
var2 = var.value()
print(var0, var1, var2)
# 1.0, 0.9, 0.71
print("步长:", var0-var1)
print("步长:", var1-var2)
# 步长: tf.Tensor(0.100000024, shape=(), dtype=float32)
# 步长: tf.Tensor(0.18, shape=(), dtype=float32)Adagrad
adagrad是对学习率修正
原始的SGD
这里
…
加上保证分母不等于0
随着迭代次数的增加,分母会越来越大,整体步学习率会越来越小。
那么从公式就能看出迭代次数小的时候,n相对来说也会小(分母也会小),那么整体的步长就会大,当迭代次数越来越多的时候,分母会逐步变大,那么迭代的整体步长就越来越小。
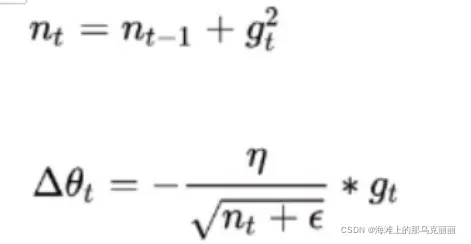
特征:
优势:
前期g较小的时候,步长就会大,就能放大梯度
后期g较大的时候,步长就会大,就能够约束梯度
缺点:
从公式可以看出,它仍然依赖于手动设置的全局学习率
后期分母上的梯度平方累加将越来越大,使g趋近于零,使训练提前结束。
# 实现adagrad梯度下降方法
# 实例化
opt = tf.keras.optimizers.Adagrad(learning_rate=0.1, initial_accumulator_value=0.1, epsilon=1e-06)
var = tf.Variable(1.0)
def loss():
return (var**2)/2.0
# 更新
opt.minimize(loss, [var])
print(var)Adadelta
adagrad的nt会不断累加,导致后期分母越来越大,整个步长越来越小,最后可能因为步长太小而不收敛的情况,adadelta为了解决这个问题加上了权重。
在Adagrad基础上在nt上加了一个权重。
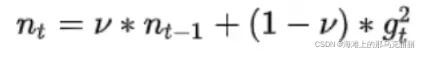
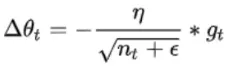
为了不依赖于全局学习率,作者对步长学习率做了一定的处理。把n*g换成了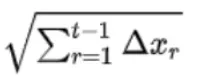 ,前面所有时刻的
,前面所有时刻的相加开根号。
分母在加权重的基础上把nt求了期望。
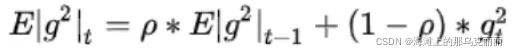
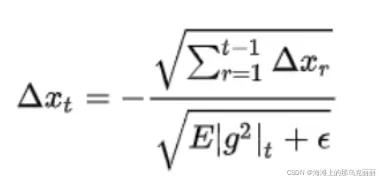
RMSprop
只是他把分子部分改回了

# 实现RMS梯度下降方法
# 实例化
opt = tf.keras.optimizers.RMSprop(learning_rate=0.1, rho=0.9)
var = tf.Variable(1.0)
def loss():
return (var**2)/2.0
# 更新
opt.minimize(loss, [var])
print(var)
Adam
adam本质上是带有动量项的RMS,就是将之前的momentum和RMSprop结合了,利用梯度的一阶估计和二阶估计动态调整每个参数的学习率。优点在于每一次迭代学习率都有一个确定范围,使得参数比较平稳。
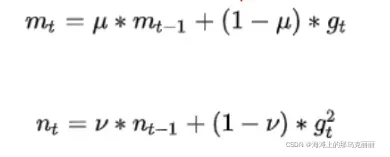
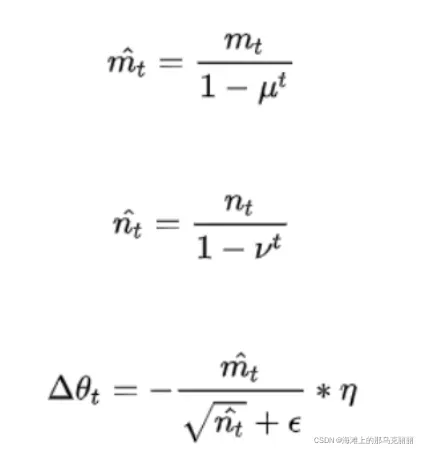
mt是动量累加公式
nt是RMSprop
结合后就是对和g同时进行调整。也就是adam的思想。
# Adam梯度下降方法
opt = tf.keras.optimizers.Adam(learning_rate=0.1)
var = tf.Variable(1.0)
def loss():
return (var**2)/2.0
# 更新
opt.minimize(loss, [var])
print(var)文章出处登录后可见!
