一、什么是交叉熵损失(Cross Entropy Loss)
交叉熵是信息论的概念。WIKIPEDIA给出的交叉熵定义如下

上面的意思大概是说,给定两个概率分布p和q,通过q来表示p的交叉熵为
![]()
其中是关于分布q的期望值算子。如果概率分布p和概率分布q是离散的,那么通过q来表示p的交叉熵为
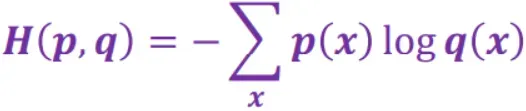
交叉熵描述了两个概率分布之间的距离。交叉熵越小,两个概率分布越接近。例如
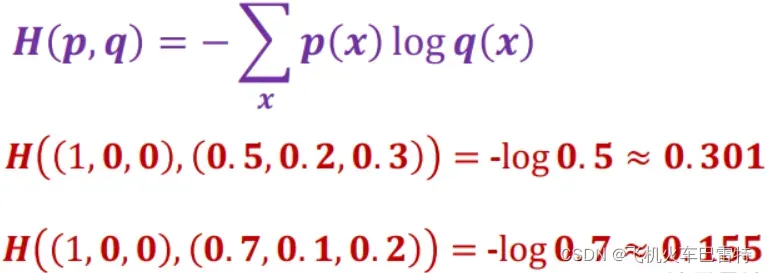
交叉熵损失定义为
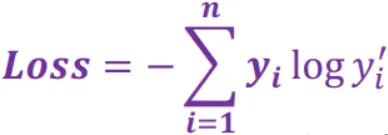
其中是标签值,
是预测值。
注意这里的预测值一般是对数据和模型参数进行一些可推导计算后得到的结果。交叉熵损失通过梯度下降不断使预测值的分布接近标签值的分布,同时模型的参数也随之更新,这在机器学习中称为学习.
二、什么是二元交叉熵损失(Binary Cross Entropy Loss)
二元交叉熵损失定义为
其中是二元标签值0或者1,
是属于
标签值的概率。
可以轻易地分析出来,当标签值时,
;当标签值
时,
。也就是说,在二元交叉熵损失函数第一项
和第二项
之中,必定有一项的值为0。我们再来看第一项和第二项的函数图像(横坐标为
,纵坐标为
):
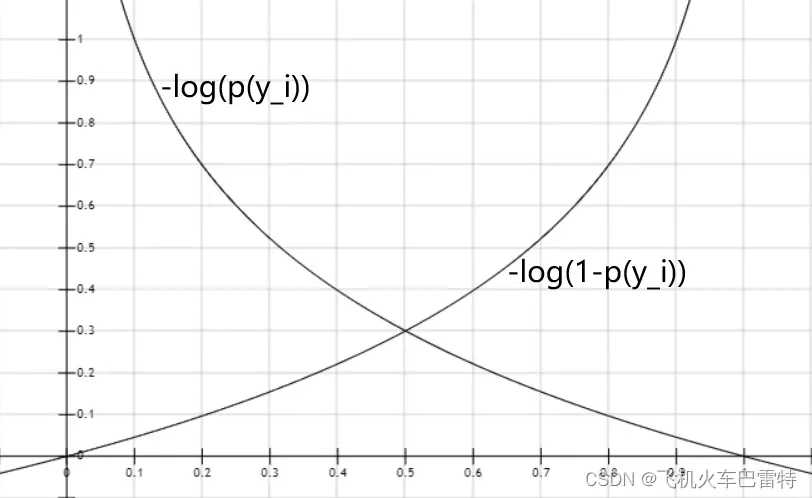
当标签值时 ,
,如果
接近1,
接近0;如果
接近0,
则变得无穷大。
当标签值时,
,如果
接近1,
变得无穷大;如果
接近0,
接近0。
通过上面的简单分析,当预测值接近标签值时,损失很小,而当预测值远离标签值时,损失很大,有利于模型的学习。
3. 参考
交叉熵损失函数
Cross Entropy
binary cross entropy in its core
文章出处登录后可见!
已经登录?立即刷新
