运动分析中的毕达哥拉斯期望，以不同运动为例

毕达哥拉斯期望用于不同的运动，如棒球、篮球、足球、曲棍球等，以驱动数据驱动的分析和预测建模

毕达哥拉斯期望是一个体育分析公式，是伟大的棒球分析师和统计学家之一 – 比尔詹姆斯的心血结晶。它最初源自棒球并为棒球而设计，最终被用于其他职业运动，如篮球、足球、美式足球、冰球等。[0]

该公式基本上表明，职业运动队在给定赛季中赢得比赛的百分比应与球队在该赛季得分/跑动/进球的平方的比值除以总和的平方和成正比。整个赛季球队和对手的得分/跑分/进球数：

这个概念不仅可以帮助解释团队为什么成功，而且可以作为预测未来结果的基础。这是一种我们可以用数据衡量的关系。我们实际上可以计算每支球队的毕达哥拉斯期望值，然后我们可以测试它是否真的与球队在给定赛季的胜率有关。

随着时间的推移，毕达哥拉斯期望公式已经根据不同的用例进行了修改和增强。修改主要集中在指数的值上。棒球案例中的理想指数被发现是 1.83 而不是 2。 Pythagenport 和 Pythagenpat 是 Bill James 原始公式的两种修改形式，已在棒球中用于计算跑步环境中的理想指数，而不是使用固定的指数值。[0][1]

同样，统计学家也研究并挖掘了其他运动的不同理想指数——篮球为 13.91，冰球为 2.37。篮球的较高指数是由于与棒球等运动相比，机会在篮球中的作用较小。

然而，在本文中，我们将深入研究毕达哥拉斯期望公式的基本形式，并了解它与不同职业运动中球队的胜率有何关系。在随后的文章中，我们还将研究毕达哥拉斯期望如何用作预测器，即我们如何使用历史毕达哥拉斯期望来预测未来的胜率。

毕达哥拉斯期望与美国职业棒球大联盟 (MLB)

我们首先将以下模块导入我们的 Jupyter Notebook：

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns

在本节中，我们将查看 2018 赛季的 MLB 比赛，可以从 Retrosheet 下载其日志。这是数据框的一瞥：[0]

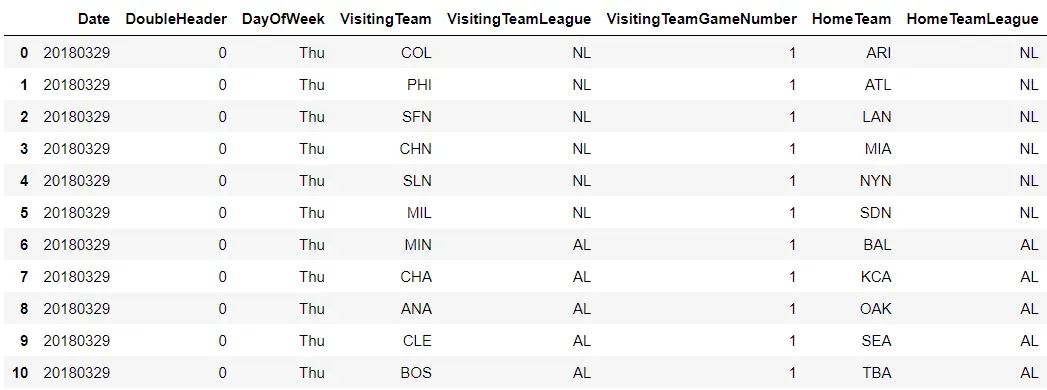
上面的屏幕截图仅涵盖前几列。 MLB 数据集中共有 161 列/特征/变量，共有 2,431 行，每行代表一个游戏。但是，对于本文，我们只需要几个列：主队、客队、主队得分、客队得分、比赛日期。为了便于使用，我们还可以将列重命名为稍短的变量名：

MLB18 = MLB[['VisitingTeam','HomeTeam','VisitorRunsScored','HomeRunsScore','Date']]
MLB18 = MLB18.rename(columns={'VisitorRunsScored':'VisR','HomeRunsScore':'HomR'})

现在，我们的数据集由单场比赛组成，每场比赛有两支球队；有主队和客队。如果我们想计算整个赛季球队得分的总数，我们需要考虑主队得分和客队得分。此外，我们需要在主队时对它进行得分，在客队时对它进行得分。为了做到这一点，我们将把这个数据框分成两个更小的数据框；一份用于客队的球队，一份用于主场球队的球队。然后我们将合并这两个数据集，以获得整个赛季每支球队的汇总数据。

在我们这样做之前，我们必须定义每场比赛的获胜者，在棒球的情况下这很简单——得分最多的球队获胜。我们可以使用 np.where Numpy 方法将胜利分为两个不同的列：主队获胜和客队获胜：

MLB18['hwin'] = np.where(MLB18['HomR'] > MLB18['VisR'],1,0)
MLB18['awin'] = np.where(MLB18['HomR'] < MLB18['VisR'],1,0)
MLB18['count'] = 1

当我们合并记录以创建一个单一的合并数据框时，将在后端使用新列 count：

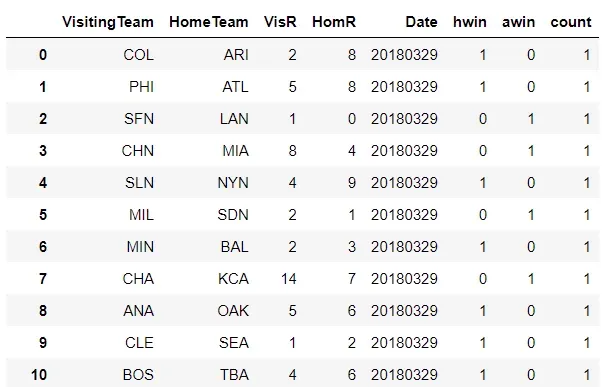
继续前进，我们现在将创建两个单独的数据框，从主队的数据框开始。我们对主队的 MLB18 数据集进行分组以获得胜利和跑分（得分和失球）的总和，以及显示打了多少场比赛的计数器变量（在 MLB 中，球队不一定打相同数量的比赛常规赛）：

MLBhome = MLB18.groupby('HomeTeam')['hwin','HomR','VisR','count'].sum().reset_index()
MLBhome = MLBhome.rename(columns={'HomeTeam':'team','VisR':'VisRh','HomR':'HomRh','count':'Gh'})

共有30支球队，其信息如下表所示：球队名称、主队胜场数、主队得分分球数、分球数客队在主队时的得分，以及该队作为主队在特定赛季中的总比赛场数。

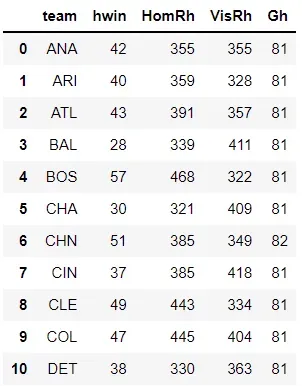
我们对客队重复同样的过程。我们从下面的代码片段中获得以下详细信息：球队名称，作为客队的球队获胜次数，作为客队的球队得分的得分，主队在对阵球队时得分的得分是客队和该队作为客队在给定赛季中的总比赛场数。

MLBaway = MLB18.groupby('VisitingTeam')['awin','HomR','VisR','count'].sum().reset_index()
MLBaway = MLBaway.rename(columns={'VisitingTeam':'team','VisR':'VisRa','HomR':'HomRa','count':'Ga'})

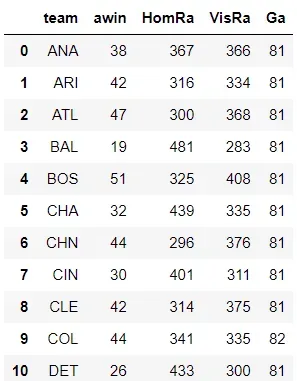
这两个数据框总结了球队作为主队和客队的表现。我们接下来需要做的是将这两个数据框合并在一起，为我们提供每支球队在整个赛季中的总体表现。为此，我们使用 pd.merge Pandas 方法将“团队”列上的两个数据框组合在一起。

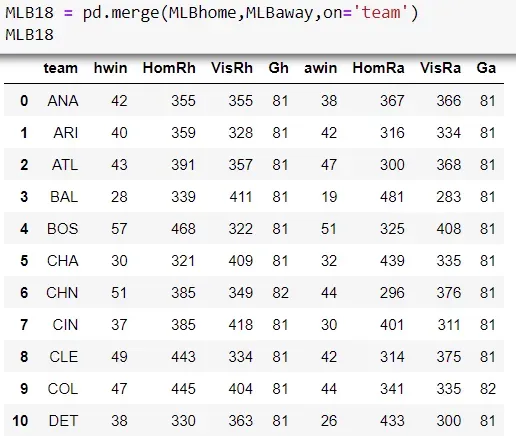
从这个合并的数据集中，我们现在可以将这些列加在一起，以获得球队在整个赛季中的总胜场数、比赛场数、得分和得分。

MLB18['W']=MLB18['hwin']+MLB18['awin']
MLB18['G']=MLB18['Gh']+MLB18['Ga']
MLB18['R']=MLB18['HomRh']+MLB18['VisRa']
MLB18['RA']=MLB18['VisRh']+MLB18['HomRa']

请注意，有 30 个不同的团队，但为了便于查看，我们将显示列表中的前 10 个：

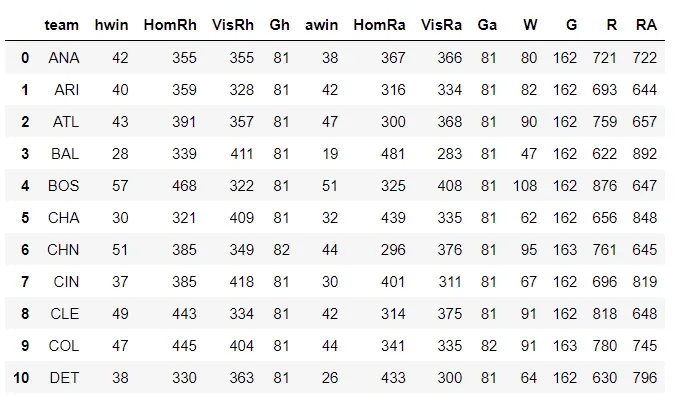
准备数据的最后一步是定义胜率和毕达哥拉斯期望。胜率只是在特定赛季中赢得的比赛总数与比赛总数的比率。

MLB18['wpc'] = MLB18['W']/MLB18['G']
MLB18['pyth'] = MLB18['R']**2/(MLB18['R']**2 + MLB18['RA']**2)ax = sns.scatterplot(x="pyth", y="wpc", data=MLB18)
plt.show()

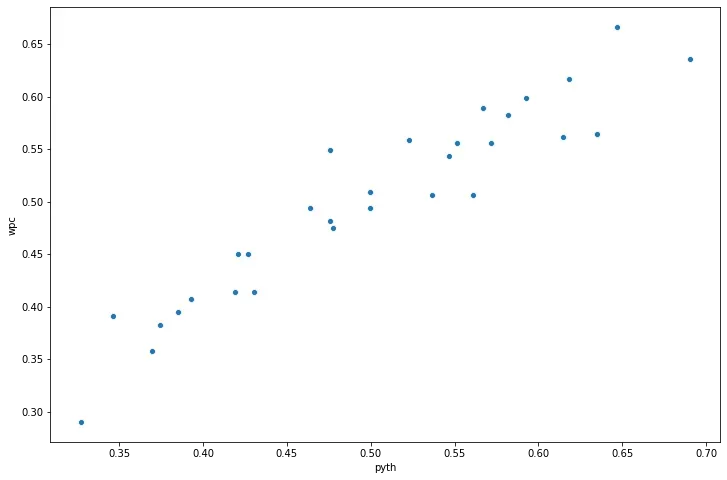
上面的散点图相当清楚地告诉我们，在我们的特定用例中，毕达哥拉斯期望值和胜率之间存在很强的相关性——毕达哥拉斯期望值越高，团队的胜率可能就越高。这证实了比尔詹姆斯所描述的关系的存在。

为了实际量化这种关系，我们可以为这种关系拟合一个回归方程，以观察毕达哥拉斯期望每增加一个单位，获胜百分比就会增加多少。

model = sm.OLS(MLB18['wpc'],MLB18['pyth'],data=MLB18)
results = model.fit()
results.summary()

回归输出告诉你很多关于胜率和毕达哥拉斯期望之间的拟合关系的信息。回归是一种识别最适合数据的方程的方法。在这种情况下，关系是：wpc = Intercept + coef x pyth

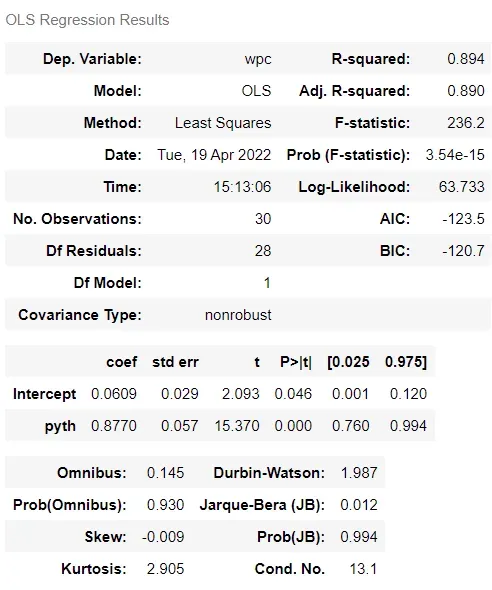
我们可以看到截距的值为 0.0609，系数为 0.8770。我们感兴趣的是后一个值。这意味着毕达哥拉斯期望每增加一个单位，胜率的值就会增加 0.877。

(i) 标准误差 (std err) 让我们了解估计的精度。系数 (coef) 与标准误差的比率称为 t 统计量 (t)，它的值告诉我们统计显着性。这可以通过 p 值 (P > |t|) 来说明——如果真实值真的为零，这是我们偶然观察到 0.8770 值的概率。这里的概率是 0.000——（这不完全是零，但表格没有包含足够的小数位来显示这一点）这意味着我们可以确信它不为零。按照惯例，通常会得出结论，如果 p 值大于 0.05，我们不能确信系数的值不为零

(ii) 表格右上角是 R 平方。该统计数据告诉您 y 变量 (wpc) 的变化百分比，这可以通过 x 变量 (pyth) 的变化来解释。 R 平方可以被认为是一个百分比——在这里，毕达哥拉斯期望可以解释 89.4% 的胜率变化。

毕达哥拉斯期望与国家篮球协会 (NBA)

以篮球为例，我们有一个具有截然不同特征的数据集。与 MLB 示例的一个重要区别是，这里每场比赛出现在两行中，每队一个，即每队每场比赛出现两次，首先作为主队，然后作为客队。所以从这个意义上说，我们的行数是游戏数的两倍。因此，我们不需要为主队和客队分开并创建两个数据框，因为在这种情况下已经为我们完成了。

数据包含 2018 赛季的比赛，这里是我们在数据框中的列/特征/变量的列表：

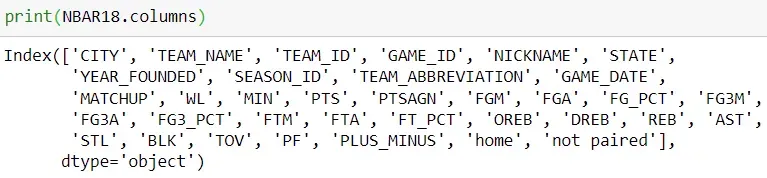
游戏结果是标有“WL”的列。我们创建一个变量，如果球队赢了，它的值为“1”，如果输了，它的值为零。现在，为了计算毕达哥拉斯期望，我们只需要结果、得分 (PTS) 和失分 (PTSAGN)。

NBAR18['result'] = np.where(NBAR18['WL']== 'W',1,0)
NBAteams18 = NBAR18.groupby('TEAM_NAME')['result','PTS','PTSAGN'].sum().reset_index()

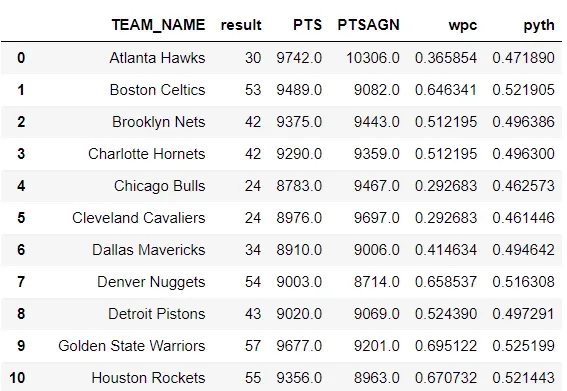
由于每支球队在一个 NBA 赛季中打了 82 场比赛，我们可以通过以下方式计算每支球队（n=30）的胜率和毕达哥拉斯期望：

NBAteams18['wpc'] = NBAteams18['result']/82
NBAteams18['pyth'] = NBAteams18['PTS']**2/(NBAteams18['PTS']**2 + NBAteams18['PTSAGN']**2)

现在，通过我们的统计分析，我们首先在 Seaborn 中创建一个散点图来查看关系是什么样的。如图所示，它看起来与棒球示例非常相似。

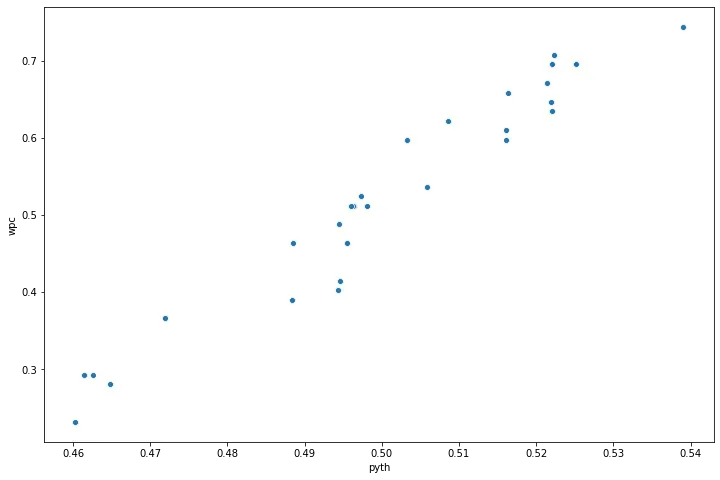
我们可以为这种关系拟合一个回归方程，以观察毕达哥拉斯期望每增加一个单位，在这个篮球示例中，胜率增加了多少。

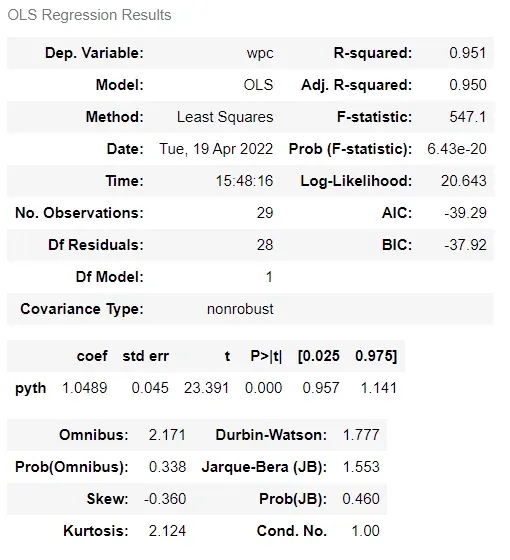
上面的结果摘要显示了非常大的 t 统计量和 0.000 的 P 值，这基本上意味着这在统计上非常显着。 R 平方（确定系数）值接近 100%，这意味着因变量 (wpc) 的几乎所有运动都完全由自变量 (pyth) 的运动来解释。

毕达哥拉斯期望和印度超级联赛（IPL）

在本文的最后一个示例中，我们将研究板球最著名的比赛 IPL 中的一个示例。我们将使用 2018 年 IPL 赛季的比赛数据，数据集包含以下列：

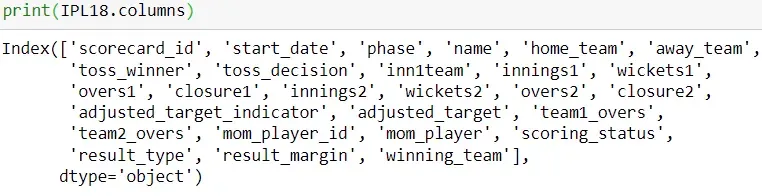
首先，我们确定主队何时是获胜队，而客队何时是获胜者。接下来我们确定主队和客队的得分（注意：与棒球不同，每支球队有九局，在 T20 板球比赛中，每支球队只有一局，一旦第一局完成，对方球队有它的一局）。最后，我们包括一个计数器，我们可以将其加起来以给出每支球队的比赛总数。

IPL18['hwin']= np.where(IPL18['home_team']==IPL18['winning_team'],1,0)
IPL18['awin']= np.where(IPL18['away_team']==IPL18['winning_team'],1,0)
IPL18['htruns']= np.where(IPL18['home_team']==IPL18['inn1team'],IPL18['innings1'],IPL18['innings2'])
IPL18['atruns']= np.where(IPL18['away_team']==IPL18['inn1team'],IPL18['innings1'],IPL18['innings2'])
IPL18['count']=1

这里要注意的一件事是 IPL18 数据框中只有 60 行（匹配）。因此，我们为板球示例所拥有的数据量明显少于我们之前介绍的篮球和棒球示例，这可能是一个潜在的问题，我们稍后会发现。

与我们在 MLB 示例中所做的类似，在 IPL 的案例中，我们也必须为主队和客队创建两个单独的数据框。我们使用相同的 .groupby 命令来汇总 2018 赛季主客队的表现，并将这两个 Data Frames 合并以获得一个组合 Data Frame，其中显示了八支 IPL 球队中每支球队的表现：

IPLhome = IPL18.groupby('home_team')['count','hwin', 'htruns','atruns'].sum().reset_index()
IPLhome = IPLhome.rename(columns={'home_team':'team','count':'Ph','htruns':'htrunsh','atruns':'atrunsh'})IPLaway = IPL18.groupby('away_team')['count','awin', 'htruns','atruns'].sum().reset_index()
IPLaway = IPLaway.rename(columns={'away_team':'team','count':'Pa','htruns':'htrunsa','atruns':'atrunsa'})IPL18 = pd.merge(IPLhome, IPLaway, on = ['team'])

这是我们需要为每支球队汇总以下数据的基本数据：获胜次数、主队获胜次数和客队获胜次数、主队和客队比赛次数、主队和客队得分，以及在主场和客场比赛时遇到：

IPL18['W'] = IPL18['hwin']+IPL18['awin']
IPL18['G'] = IPL18['Ph']+IPL18['Pa']
IPL18['R'] = IPL18['htrunsh']+IPL18['atrunsa']
IPL18['RA'] = IPL18['atrunsh']+IPL18['htrunsa']

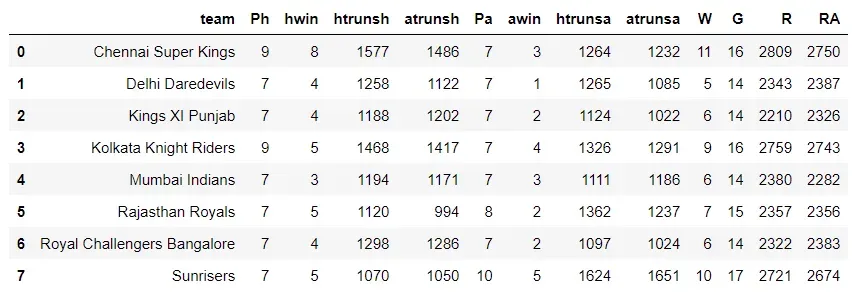
现在可以轻松计算获胜百分比，即获胜次数除以比赛次数，以及毕达哥拉斯期望，即得分平方除以得分平方和得分平方和的总和：

IPL18['wpc'] = IPL18['W']/IPL18['G']
IPL18['pyth'] = IPL18['R']**2/(IPL18['R']**2 + IPL18['RA']**2)

准备好数据后，我们现在准备使用散点图检查因变量和自变量之间的关系。

我们可以看到，胜率与毕达哥拉斯期望之间的相关性非常弱。首先，因为我们只有 8 个团队，所以我们的点要少得多，所以当你的数据中的观察值如此之少时，就很难辨别任何关系。第二点要注意的是，这些点往往分散在整个情节中，它们并没有像我们在前两个例子中看到的那样以向上倾斜的关系从左到右整齐地组织起来。

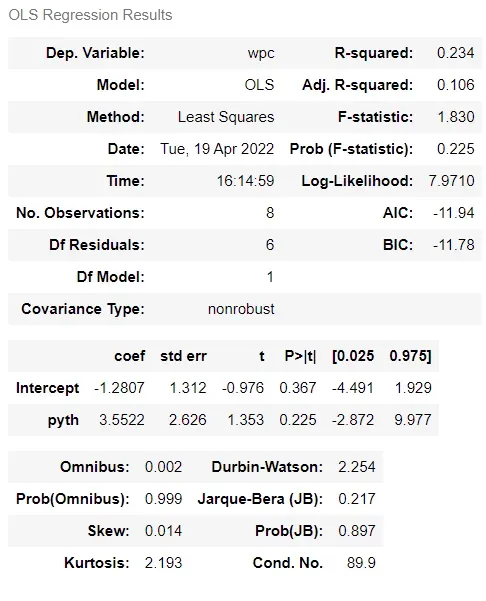
当我们在这种关系上拟合线性回归模型时，这一点得到了进一步证实。这一次，虽然 pyth 上的系数为正 – 意味着较高的毕达哥拉斯期望会导致较大的获胜百分比，但标准误差也非常大，1.353 的 t 统计量意味着 p 值为 0.225 – 远高于通常的阈值0.05。反过来，这意味着系数估计实际上与零的差异微不足道，我们可以自信地说，在 IPL 示例中，毕达哥拉斯期望与获胜百分比之间没有统计学上的显着关系。

毕达哥拉斯期望模型对 IPL 数据集没有产生好的结果可能有几个原因。首先，如上所述，我们拥有的 IPL 数据非常有限：60 场比赛和 8 支球队，而 MLB 大约有 2,300 场比赛和 30 支球队。在大规模分析数据时可能会消除随机变化，因此如果在 IPL 示例中它是正确的，那么随机变化可能会压倒毕达哥拉斯模型的可能性要大得多。

另一种解释可能是板球和棒球等运动之间存在一些根本差异，这使得毕达哥拉斯模型适用于其中之一，但不适用于另一个。例如，在板球比赛中，第二名击球手只需比对手多得分一分即可获胜，因此如果达到这一里程碑，则该局结束。如果第二个击球的球队是获胜的球队，那么比分差距就会很小。但是，如果先击球的球队可以便宜地获得全部十个三柱门，那么得分差距可能会很大。在我们的数据中，第二次击球获胜的球队的平均跑分差异为 2，而第一次击球的球队获胜时的平均跑数差异为 30。这种不对称性解释了为什么毕达哥拉斯期望可能不是在 IPL 中获胜的良好指南。

也许，我们可以在另一篇文章中研究数据局，并尝试分析获胜球队分别先击球或后击球的比赛。目前，本文到此结束。在接下来的文章中，我们将研究毕达哥拉斯期望如何在英超联赛 (EPL) 中用作预测器。

References:

1. 体育分析的基础：体育中的数据、表示和模型[0]
2. 棒球参考[0]
3. 毕达哥拉斯期望[0]
4. 来自 Retrosheet 的数据集（许可证：https://www.retrosheet.org/notice.txt）[0][1]