2.7 计算图(Computation Graph)
可以说,神经网络的计算是按照前向或反向传播过程来组织的。首先我们计算一个新网络的输出(正向过程),然后是反向传输操作。后者我们用来计算相应的梯度或导数。计算图解释了为什么我们以这种方式组织这些计算。在本视频中,我们将举例说明什么是计算图。让我们举一个比逻辑回归更简单或形式化程度更低的神经网络的例子。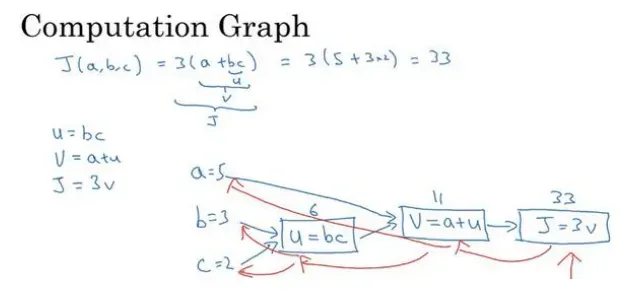
我们尝试计算函数𝐽,𝐽是由三个变量𝑎, 𝑏, 𝑐组成的函数,这个函数是3(a + bc) 。计算这个函数实际上有三个不同的步骤,首先是计算 𝑏 乘以 𝑐,我们把它储存在变量𝑢中,因此𝑢 = 𝑏𝑐; 然后计算𝑣 = 𝑎 + 𝑢;最后输出𝐽 = 3𝑣,这就是要计算的函数𝐽。我们可以把这三步画成如下的计算图,我先在这画三个变量𝑎, 𝑏, 𝑐,第一步就是计算𝑢 = 𝑏𝑐,我在这周围放个矩形框,它的输入是𝑏, 𝑐,接着第二步𝑣 = 𝑎 + 𝑢,最后一步𝐽 = 3𝑣。
举个例子: 𝑎 = 5, 𝑏 = 3, 𝑐 = 2 ,𝑢 = 𝑏𝑐就是 6,就是 5+6=11。𝐽是 3 倍的 ,因此。即3 × (5 + 3 × 2)。如果你把它算出来,实际上得到 33 就是𝐽的值。 当有不同的或者一些特殊的输出变量时,例如本例中的𝐽和逻辑回归中你想优化的代价函数𝐽,因此计算图用来处理这些计算会很方便。从这个小例子中我们可以看出,通过一个从左向右的过程,你可以计算出𝐽的值。为了计算导数,从右到左(红色箭头,和蓝色箭头的过程相反)的过程是用于计算导数最自然的方式。
回顾一下:计算图以蓝色箭头从左到右计算的形式组织计算,让我们在下一个视频中看看反向红色箭头(也就是从右到左)的导数计算是如何完成的,让我们继续学习在下一个视频中。
2.8 使用计算图求导数(Derivatives with a Computation Graph)
在上一个视频中,我们看到了一个使用流计算图 𝐽 计算函数的示例。现在让我们看一下流程图的描述,看看如何使用它来计算函数𝐽的导数。
下面使用的公式:
下面使用的公式:
文章出处登录后可见!