假设检验中的统计功效——视觉解释

青葱年少

2 年前

Table of Contents

假设检验中的统计功效——视觉解释

权力是什么/为什么/如何的互动指南

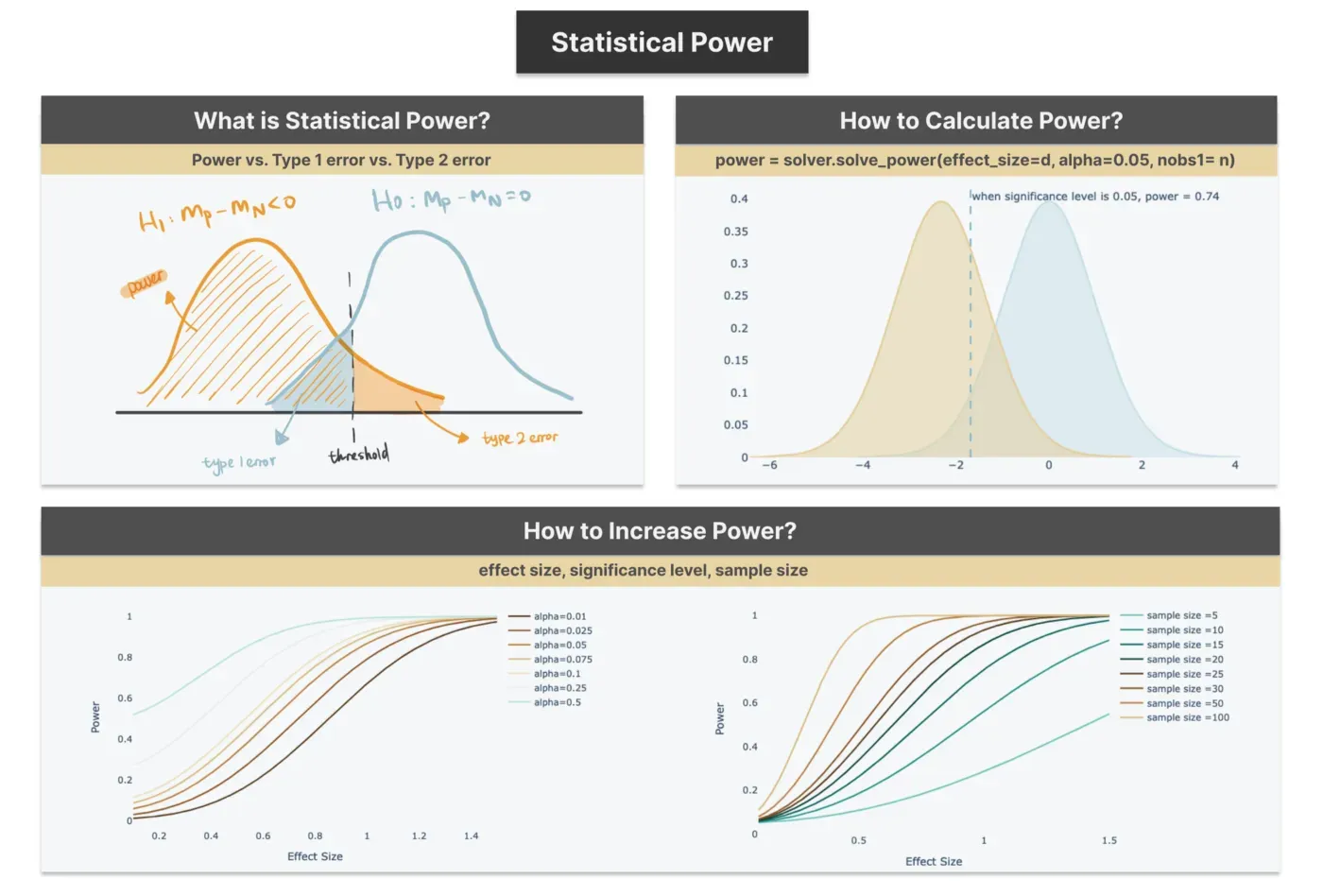
什么是统计能力？

统计功效是假设检验中的一个概念，它计算当效应实际上为正时检测到正效应的概率。在我之前的帖子中，我们介绍了进行假设检验的程序。在这篇文章中，我们将在此基础上在假设检验中引入统计功效。[0]

电源和类型 1 错误和类型 2 错误

在谈到 Power 时，似乎不可避免地还会提到 Type 1 和 Type 2 错误。它们都是众所周知的假设检验概念，用于将预测结果与实际结果进行比较。

让我们继续使用我之前的文章“假设检验的交互式指南”中的 t 检验示例来说明这些概念。[0]

回顾：我们使用单尾二样本 t 检验来比较两个客户样本——接受活动报价的客户和拒绝活动报价的客户。

recency_P = df[df['Response']==1]['Recency'].sample(n=20, random_state=100)
recency_N = df[df['Response']==0]['Recency'].sample(n=20, random_state=100)

零假设（H0）：接受报价的客户和不接受报价的客户之间的新近度没有差异——如下面的蓝线所示。
替代假设（H1）：接受报价的客户与不接受报价的客户相比具有较低的新近度——如下面的橙色线所示。

类型 1 错误（假阳性）：如果值落在图表中的蓝色区域内，即使它们在原假设为真时发生，我们也会选择拒绝原假设，因为它们低于阈值。结果，我们犯了第 1 类错误或误报错误。它与显着性水平（通常为 0.05）相同，这意味着我们允许 5% 的风险声称接受报价的客户具有较低的新近度，而实际上没有差异。类型 1 错误的结果是，公司可能会向 Recency 值低但响应率不佳的人发送新的活动报价。

类型 2 错误（假阴性）：如橙色区域中突出显示的那样，当备择假设实际上为真时，它是拒绝替代假设的概率——因此，当实际存在差异时，声称两组之间没有差异。与在业务环境中一样，营销团队可能会失去具有高投资回报的潜在目标活动机会。

统计功效（真阳性）：当备择假设为真时正确接受它的概率。它与类型 2 错误完全相反：Power = 1 — 类型 2 错误，我们正确地预测，与不接受该报价的客户相比，接受该报价的客户更有可能具有较低的 Recency。

将鼠标悬停在下面的图表上，您将看到当我们应用不同的阈值时功率、类型 1 错误和类型 2 错误如何变化。（如果您想自己构建，请查看我网站上的代码片段部分）[0]

为什么要使用统计能力？

显着性水平广泛用于确定假设检验的统计显着性。然而，它只讲述了故事的一部分——尽量避免声称存在真正的影响/差异，因为不存在实际差异。一切都基于零假设为真的假设。如果我们想看到故事的积极方面——当备择假设为真时做出正确结论的概率呢？我们可以使用电源。

此外，Power 还在确定样本量方面发挥作用。较小的样本量可能会偶然给出较小的 p 值，这表明它不太可能是误报错误。但这并不能保证有足够的证据证明真阳性。因此，通常在实验之前定义功效，以确定为检测实际效果提供足够证据所需的最小样本量。

如何计算功率？

功效的大小受三个因素的影响：显着性水平、样本量和效应量。 Python 函数solve_power() 计算给定参数值的功率——effect_size、alpha、nobs1。

让我们使用上面的 Customer Recency 示例进行功率分析。

from statsmodels.stats.power import TTestIndPower
t_solver = TTestIndPower()
power = t_solver.solve_power(effect_size=recency_d, alpha=0.05, power=None, ratio=1, nobs1= 20, alternative='smaller')

显着性水平：我们将 alpha 值设置为 0.05，这也确定了 Type 1 错误率为 5%。 Alternative=‘smaller’是指定备择假设：两组的平均差小于0。
样本大小：nobs1 指定样本 1（20 个客户）的大小，比率是样本 2 中相对于样本 1 的观察数。
效应大小： effect_size 计算为相对于合并标准差的平均差之间的差。对于两个样本的 t 检验，我们使用 Cohen 的 d 公式来计算效应大小。我们得到了 0.73。通常，0.20、0.50、0.80 和 1.3 被认为是小、中、大和非常大的效应大小。

# calculate effect size using Cohen's d
n1 = len(recency_N)
n2 = len(recency_P)
m1, m2 = mean(recency_N), mean(recency_P)
sd1, sd2 = np.std(recency_N), np.std(recency_P)
pooled_sd = sqrt(((n1 - 1) * sd1**2 + (n2 - 1) * sd2**2) / (n1 + n2 - 2))
recency_d = (m2 - m1)/pooled_sd

如上图“Power, Type1 error and Type2 error”交互图所示，显着性水平为0.05时，功效为0.74。

如何提高统计能力？

功效与效应量、显着性水平和样本量呈正相关。

1. Effect Size

较大的效应大小表示相对于合并标准差的平均值差异较大。当效应量增加时，表明两个样本数据之间存在更多观察到的差异。因此，当它提供更多证据证明替代假设为真时，Power 会增加。将鼠标悬停在线条上以查看功率如何随着效果大小的变化而变化。

2. 显着性水平/I 类错误

类型 1 错误和类型 2 错误之间存在权衡，因此如果我们允许更多类型 1 错误，我们也会增加功率。如果您将鼠标悬停在第一个交互式图表“功率、类型 1 和类型 2 错误”中的线条上，您会注意到当我们尝试减轻类型 1 错误时，类型 2 错误会增加而功率会降低。这是因为如果最大限度地减少误报错误，我们就会提高标准并为我们可以归类为积极影响的内容添加更多限制。当标准太高时，我们也在降低正确分类积极效果的概率。因此，我们无法使它们都完美。因此，应用了一个常见阈值，即类型 1 错误 0.05 和功率 – 0.8，以平衡这种权衡。