前言

实际上本次例题涉及的杜教筛不麻烦，麻烦的是例题的式子的推导与变换，后续更新其他例题，陆续更新博客内容~

涉及前置知识点：线性筛求积性函数，整除分块，积性函数的性质，狄利克雷卷积

一、前置知识

1.杜教筛解决什么问题？

解决积性函数求前缀和的问题，它可以在非线性时间内求积性函数前缀和。为什么要使用杜教筛？不能用线性筛筛积性函数吗？
答：线性筛只适用于1e8以下的求积性函数前缀和问题，因为复杂度是O(n),而当n>1e9时，就会超时，而杜教筛可以解决n = 1e11的积性函数求前缀和问题，杜教筛算法的时间复杂度是

2. 积性函数与线性筛求积性函数

积性函数：对于任意互质的整数 a,b有 f(a×b)=f(a)×f(b)的数论函数。

完全积性函数：对于任意整数 a,ba,b 有 f(a×b)=f(a)×f(b)的数论函数。

常见的积性函数:

3.狄利克雷卷积

​狄利克雷卷积满足交换律和结合律

结合狄利克雷卷积得到的几个积性函数之间性质：

4.整除分块

详情见另一篇博客：整除分块笔记1

二、杜教筛

1.式子推导

这里给出杜教筛的式子推导：

2.例题

2.1 例题一

luoguP4213
求：

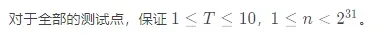
2.1.1 问题分析

P4213题解的第一篇题解里有杜教筛时间复杂度的证明。
再由积性函数的性质有：

根据杜教筛推导公式以及设定要求的函数：

2.1.2 代码实现

#include<iostream>
#include<cstdio>
#include<map>
using namespace std;
typedef long long ll;
ll t,n;
const ll N = 5e6+10;//注意一定要把N开到比筛的范围多一些，不然会爆
ll primes[N];
ll phi[N],mu[N];
bool st[N];
map<ll,ll>ans_phi;
map<ll,ll>ans_mu;
//虽然可以直接杜教筛，核心内容就是推公式+整除分块，但是很慢呜呜呜
//正常的杜教筛步骤：
//1.开始硬推公式
//2.套用杜教筛核心公式
//3.O(n)预处理一个想求的函数的前缀和,大概5e7，这一步就是降时间复杂度的
//据说能O(n^(3/4))->O(n^(2/3))证明不会呜呜呜
void init(ll n)
{
//欧拉筛求积性函数，关于欧拉筛求积性函数会另外写一篇博客
    ll cnt = 0;
    phi[1] = 1,mu[1] = 1;
    for(ll i = 2;i<=n;i++)
    {
        if(!st[i])
        {
            primes[cnt++] = i;
            mu[i] = -1;
            phi[i] = i-1;//由定义出发
        }
        for(ll j = 0;j<cnt&&i*primes[j]<=n;j++)
        {
            st[i*primes[j]] = true;
            if(i%primes[j]==0)
            {
                phi[i*primes[j]] = phi[i]*primes[j];
                mu[i*primes[j]] = 0;
                break;
            }
            else
            {
                phi[i*primes[j]] = phi[i]*phi[primes[j]];
                mu[i*primes[j]] = -mu[i];
            }
        }
    }
    //前缀和累加
    for(ll i = 1;i<=n;i++)
        phi[i]+= phi[i-1];
    for(int i = 1;i<=n;i++)
        mu[i] += mu[i-1];
}

ll phiSum(ll n)
{
    if(n<=N) return phi[n];
    if(ans_phi[n]) return ans_phi[n];
    ll ans = n*(n+1)/2;
    //主要l从2开始，第一项是S(n)
	//这里是整除分块，
    for(ll l = 2,r;l<=n;l = r+1){
        r = (n/(n/l));
        ans-=(r-l+1)*phiSum(n/l);
    }
    return ans_phi[n] = ans;//记忆化加速
}
ll muSum(ll n)
{
    if(n<=N) return mu[n];
    if(ans_mu[n]) return ans_mu[n];
    ll ans = 1;
    //主要l从2开始，第一项是S(n)
    for(ll l = 2,r;l<=n;l = r+1){
        r = (n/(n/l));
        ans-=(r-l+1)*muSum(n/l);
    }
    return ans_mu[n] = ans;//记忆化加速
}
int main()
{
    scanf("%lld",&t);
    init(N);
    while(t--)
    {
        scanf("%lld",&n);
        printf("%lld %lld\n",phiSum(n),muSum(n));
    }
    return 0;
}

2.2 例题二

求:

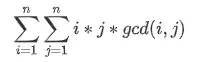
2.2.1 式子推导：

2.2

2.3 继续推导

接2.1

2.4 代码实现

三、总结

未完待续～代码后续更新~