整理GIS基础知识,投影,坐标系问题。
1. 大地测量学 (Geodesy)
大地测量学是一门量测和描绘地球表面的学科,也包括确定地球重力场和海底地形。
1.1 大地水准面 (geoid)
大地水准面是海洋表面在排除风力、潮汐等其它影响,只考虑重力和自转影响下的形状,这个形状延伸过陆地,生成一个密闭的曲面。虽然我们通常说地球是一个球体或者椭球体,但是由于地球引力分布不均(因为密度不同等原因),大地水准面是一个不规则的光滑曲面。虽然不规则,但是可以近似地表示为一个椭球体,这个椭球体被 称为参考椭球体(Reference ellipsoid)。大地水准面相对于参考椭球体的高度被称为 Undulation of the geoid 。这个波动并不是非常大,最高在冰岛为85m,最低在印度南部为 −106 m,一共不到200m。下图来自维基百科,表示 EGM96 geoid 下不同地区的 Undulation。
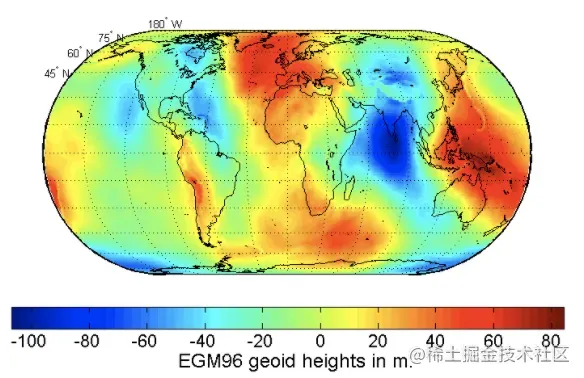
1.2 参考椭球体(Reference ellipsoid)
参考椭球体(Reference ellipsoid)是一个数学上定义的地球表面,它近似于大地水准面。因为是几何模型,可以用长半轴、短半轴和扁率来确定。我们通常所说的经度、纬度以及高度都以此为基础。
一方面,我们对地球形状的测量随着时间迁移而不断精确,另一方面,因为大地水准面并不规则,地球上不同地区往往需要使用不同的参考椭球体,来尽可能适合当地的大地水准面。历史上出现了很多不同的参考椭球体,很多还仍然在使用中。国内过去使用过“北京54”和“西安90”两个坐标系,其中北京54使用的是克拉索夫斯基(Krasovsky)1940的参考椭球,西安80使用的是1975年国际大地测量与地球物理联合会第16届大会推荐的参考椭球。当前世界范围内更普遍使用的是WGS所定义的参考椭球。
2. 坐标系(coordinate system)
有了参考椭球体这样的几何模型后,就可以定义坐标系来进行描述位置,测量距离等操作,通常有两种坐标系 地理坐标系(geographic coordinate systems) 和 投影坐标系(projected coordinate systems)。
2.1 地理坐标系(Geographic coordinate system)
地理坐标系一般是指由经度、纬度和高度组成的坐标系,能够标示地球上的任何一个位置。
前面提到了,不同地区可能会使用不同的参考椭球体,即使是使用相同的椭球体,也可能会为了让椭球体更好地吻合当地的大地水准面,而调整椭球体的方位,甚至大小。这就需要使用不同的大地测量系统(Geodetic datum)来标识。
因此,对于地球上某一个位置来说,使用不同的测量系统,得到的坐标是不一样的。我们在处理地理数据时,必须先确认数据所用的测量系统。
事实上,随着我们对地球形状测量的越来越精确,北美使用的 NAD83 基准和欧洲使用的 ETRS89 基准,与 WGS 84 基准是基本一致的,甚至我国的 CGCS2000 与WGS84之间的差异也是非常小的。但是差异非常小,不代表完全一致,以 NAD83 为例,因为它要保证北美地区的恒定,所以它与 WGS84 之间的差异在不断变化,对于美国大部分地区来说,每年有1-2cm的差异。
2.1.1 地理坐标系的列举
我们通常用经纬度来表示一个地理位置,但是由于一些原因,我们从不同渠道得到的经纬度信息可能并不是在同一个坐标系下。
- 高德地图、腾讯地图以及谷歌中国区地图使用的是GCJ-02坐标系
- 百度地图使用的是BD-09坐标系
- 底层接口(HTML5 Geolocation或ios、安卓API)通过GPS设备获取的坐标使用的是WGS-84坐标系
不同的坐标系之间可能有几十到几百米的偏移,所以在开发基于地图的产品,或者做地理数据可视化时,我们需要修正不同坐标系之间的偏差。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mDr8fT9Z-1652148469330)(https://p1-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/74f0f75eac99497482d57ca31471850c~tplv-k3u1fbpfcp-watermark.image)]
2.1.2 WGS-84 – 世界大地测量系统
WGS-84(World Geodetic System, WGS)是使用最广泛的坐标系,也是世界通用的坐标系,别名有:WGS:1984、EPSG:4326。
GPS设备得到的经纬度就是在WGS84坐标系下的经纬度。
通常通过底层接口得到的定位信息都是WGS84坐标系。
全球除神州外,几乎所有地图商都是使用这个坐标系,比如Google地图使用的就是WGS84坐标。
2.1.3 GCJ-02 – 国测局坐标系
GCJ-02(G-Guojia国家,C-Cehui测绘,J-Ju局),又被称为火星坐标系,是一种基于WGS-84制定的大地测量系统,由中国国测局制定。此坐标系所采用的混淆算法会在经纬度中加入随机的偏移。
由中国国家测绘局制定的地理信息系统的坐标,国内出版的各种地图坐标系统(包括电子地图),必须至少采用GCJ02对WGS84进行首次加密。
GCJ-02坐标系应用的一些地图列举:google中国地图、soso地图、aliyun地图、mapabc地图和高德地图等。
🚨 注意:
国家规定,中国大陆所有公开地理数据都需要至少用GCJ-02进行加密,也就是说我们从国内公司的产品中得到的数据,一定是经过了加密的。绝大部分国内互联网地图提供商都是使用GCJ-02坐标系,包括高德地图,谷歌地图中国区等。
导航电子地图在公开出版、销售、传播、展示和使用前,必须进行空间位置技术处理。 — GB 20263―2006《导航电子地图安全处理技术基本要求》,4.1
2.1.4 BD-09 – 百度坐标系
BD-09(Baidu, BD)是百度地图使用的地理坐标系,其在GCJ-02上多增加了一次变换,用来保护用户隐私。从百度产品中得到的坐标都是BD-09坐标系。
2.1.5 CGCS2000 – 国家大地坐标系
2000国家大地坐标系,是我国当前最新的国家大地坐标系,英文名称为China Geodetic Coordinate System 2000,英文缩写为CGCS2000。
2000国家大地坐标系的原点为包括海洋和大气的整个地球的质量中心;2000国家大地坐标系的Z轴由原点指向历元2000.0的地球参考极的方向,该历元的指向由国际时间局给定的历元为1984.0的初始指向推算,定向的时间演化保证相对于地壳不产生残余的全球旋转,X轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点,Y轴与Z轴、X轴构成右手正交坐标系。采用广义相对论意义下的尺度。
2.1.6 地理坐标系相互转换
GCJ-02和BD-09都是用来对地理数据进行加密的,所以也不会公开逆向转换的方法。理论上,GCJ-02的加密过程是不可逆的,但是可以通过一些方法来逼近接原始坐标,并且这种方式的精度很高。gcoord使用的纠偏方式达到了厘米级的精度,能满足绝大多数情况。
2.2 投影坐标系(Projected coordinate systems)
一个投影坐标系统就是定义了如何将一个三维的模型转换为一个二维的平面(这样相比于地球仪更容易携带),这个在数学上被称为投影。
地理坐标系是三维的,我们要在地图或者屏幕上显示就需要转化为二维,这被称为投影(Map projection)。显而易见的是,从三维到二维的转化,必然会导致变形和失真,失真是不可避免的,但是不同投影下会有不同的失真,这让我们可以有得选择。常用的投影有等矩矩形投影(Platte Carre)和墨卡托投影(Mercator),下图来自Mercator vs. well…not Mercator (Platte Carre),生动地说明了这两种投影下的失真:
左图表示地球球面上大小相同的圆形,右上为墨卡托投影,投影后仍然是圆形,但是在高纬度时物体被严重放大了。右下为等距投影,物体的大小变化不是那么明显,但是图像被拉长了。等矩矩形投影(Platte Carre)因为在投影上有扭曲,并不适合于航海等活动,但是因为坐标与像素之间的对应关系十分简单,非常适合于栅格图的展示,等矩矩形投影(Platte Carre)是很多GIS软件的默认投影。
需要注意的是,对于墨卡托投影来说,越到高纬度,大小扭曲越严重,到两极会被放到无限大,所以,墨卡托投影无法显示极地地区。下图来自维基百科,可以看到墨卡托投影下每个国家的大小和实际大小的差异。但是 conformality(正形性) 和 straight rhumb lines 这两个特点,让它非常适合于航海导航。
投影变形的形式:角度变形、长度变形和面积变形。
地图投影的方式:
- 等角投影——投影前后的角度相等,但长度和面积有变形;
- 等距投影——投影前后的长度相等,但角度和面积有变形;
- 等积投影——投影前后的面积相等,但角度和长度有变形。
还要了解一点,投影坐标系的基础是地理坐标系,没有地理坐标系,也就没有所谓的投影坐标系,投影坐标系是地理坐标系上的地物投射到具体投影面上的一种结果。
2.2.1 投影坐标系的列举
- 墨卡托投影
- 高斯-克吕格投影
- 通用横轴墨卡托投影
- web墨卡托投影(Web Mercator) EPSG:3857
2.3 CGCS2000与WGS84、北斗坐标系的区别
摘要:CGCS2000和1954或1980坐标系,在定义和实现上有根本区别。局部坐标和地心坐标之间的变换是不可避免的。坐标变换通过联合平差来实现。当采用模型变换时,变换模型的选择应依据精度要求而定。
CGCS2000是中国2000国家大地坐标系的缩写,该坐标系是通过中国GNSS 连续运行基准站、 空间大地控制网以及天文大地网联合平差建立的地心大地坐标系统。2000国家大地坐标系以ITRF 97 参考框架为基准, 参考框架历元为2000.0。
CGCS2000坐标系原点和轴定义如下:原点为地球的质量中心;Z轴指向IERS参考极方向;X轴为IERS参考子午面与通过原点且同Z轴正交的赤道面的交线;Y轴完成右手地心地固直角坐标系。
2000国家大地坐标系的大地测量基本常数分别为: 长半轴 a = 6 378 137 m; 地球引力常数 GM =3.986004418×1014m3s-2; 扁率f = 1/ 298. 257 222 101;地球自转角速度X =7.292115×10-5rad s-1
2.3.1 与WGS84区别
CGCS2000的定义与WGS84实质一样,原点、尺度、定向均相同,都属于地心地固坐标系。采用的参考椭球非常接近。扁率差异引起椭球面上的纬度和高度变化最大达0.1mm。当前测量精度范围内,两者相容至cm级水平。
CGCS2000坐标是2000.0历元的瞬时坐标,而WGS84坐标是观测历元的动态坐标,两者都基于ITRF框架,可通过历元、框架转换进行换算。同样的点位及观测精度,GNSS接收机获取的WGS84坐标及CGCS2000坐标并不是只有厘米级的差异,而是因框架、历元差异产生的分米级的坐标差。历元归算到2000.0的WGS坐标,可以作为CGCS2000坐标使用。
WGS84坐标系由26个全球分布的监测站坐标来实现,不同版本的WGS84对应相应的ITRF版本和参考历元。
2.3.2 与北斗坐标系区别
北斗坐标系和WGS84坐标系类似,属于导航坐标系,其坐标是观测历元的动态坐标,与CGCS2000坐标系有2500多个框架点不同,北斗坐标系只有几个框架点,其更新周期短,测量精度低,而CGCS2000属于国家基础坐标系,更新周期往往长达几十年。但CGCS2000坐标系与北斗坐标系的定义、椭球是一致的,
2.3.3 与54系、80系区别
CGCS2000和1954或1980坐标系,在定义和实现上有根本区别。局部坐标和地心坐标之间的变换是不可避免的。坐标变换通过联合平差来实现。当采用模型变换时,变换模型的选择应依据精度要求而定。
2.4 说明
测绘工作中采用的RTK、静态测量等属于相对定位,以地面已知控制点做起算,所以相对定位成果的历元和框架由控制点坐标的历元和框架决定;精密单点定位等绝对定位是以卫星星历作为起算数据,而卫星星历是利用地面监测站的卫星跟踪数据计算得到。
坐标框架体系建设历史及来源: 20世纪50年代,为满足测绘工作的迫切需要 ,中国采用 了1954年北京坐标系。1954年之后,随着天文大地网布设任务的完成,通过天文大地网整体平差,于20世纪80年代初中国又建立了1980西安坐标系。1954北京坐标系和1980西安坐标系在中国的经济建设和国防建设中发挥了巨大作用。
随着情况的变化和时间的推移,上述两个以经典测量技术为基础的局部大地坐标系,已经不能适应科学技术特别是空间技术发展,不能适应中国经济建设和国防建设需要。中国大地坐标系的更新换代,是经济建设、国防建设、社会发展和科技发展的客观需要。
以地球质量中心为原点的地心大地坐标系,是21世纪空间时代全球通用的基本大地坐标系。以空间技术为基础的地心大地坐标系,是中国新一代大地坐标系的适宜选择。历经多年,中国测绘、地震部门和科学院有关单位为建立中国新一代大地坐标系作了大量基础性工作,20世纪末先后建成全国 GPS一、二级网,国家GPS A、B级网,中国地壳运动观测网络和许多地壳形变网,为地心大地坐标系的实现奠定了较好的基础。中国大地坐标系更新换代的条件也已具备。中国新一代大地坐标系建立的基本原则是:
1)坐标系应尽可能对准 ITRF(国际地球参考框架);
2)坐标系应由空间大地网在某参考历元的坐标和速度体现;
3)参考椭球的定义参数选用长半轴、扁率、地球地心引力常数和地球角速度,其参数值采用 IUGG (国际大地测量与地球物理联合会)或 IERS(国际地球旋转与参考系服务局)的采用值或推荐值。
3. 对于 Web Map 开发人员的意义
对于 Web Map 开发人员来说,最熟悉的应该是EPSG:4326 (WGS84) and EPSG:3857(Pseudo-Mercator),这又是啥呢?
3.1 EPSG:4326 (WGS84)
前面说了 WGS84 是目前最流行的地理坐标系统。在国际上,每个坐标系统都会被分配一个 EPSG 代码,EPSG:4326 就是 WGS84 的代码。GPS是基于WGS84的,所以通常我们得到的坐标数据都是WGS84的。一般我们在存储数据时,仍然按WGS84存储。
3.2 EPSG:3857 (Pseudo-Mercator)
伪墨卡托投影,也被称为球体墨卡托,Web Mercator。它是基于墨卡托投影的,把 WGS84坐标系投影到正方形。我们前面已经知道 WGS84 是基于椭球体的,但是伪墨卡托投影把坐标投影到球体上,这导致两极的失真变大,但是却更容易计算。这也许是为什么被称为”伪“墨卡托吧。另外,伪墨卡托投影还切掉了南北85.051129°纬度以上的地区,以保证整个投影是正方形的。因为墨卡托投影等正形性的特点,在不同层级的图层上物体的形状保持不变,一个正方形可以不断被划分为更多更小的正方形以显示更清晰的细节。很明显,伪墨卡托坐标系是非常显示数据,但是不适合存储数据的,通常我们使用WGS84 存储数据,使用伪墨卡托显示数据。
Web Mercator 最早是由 Google 提出的,当前已经成为 Web Map 的事实标准。但是也许是由于上面”伪“的原因,最初 Web Mercator 被拒绝分配EPSG 代码。于是大家普遍使用 EPSG:900913(Google的数字变形) 的非官方代码来代表它。直到2008年,才被分配了EPSG:3785的代码,但在同一年没多久,又被弃用,重新分配了 EPSG:3857 的正式代码,使用至今。
3.3 国内地图坐标使用注意事项
火星坐标与地球通用坐标系WGS84,偏差一般为 300~500 米。也就是说,你手机GPS获取的坐标,直接叠加到这个“火星坐标系”的地图上,会有 300~500 米的偏差。偏移的絕對值可以參見下圖(最紅處接近 700 m,最藍處大約 20 米):
具体参考:
如何看待「地形图非线性保密处理技术」? https://www.zhihu.com/question/29806566/answer/46099380
4 常用地图坐标系之间的转换(SQL)
4.1 大地坐标系2000转EPSG:4326 (WGS84)
st_setsrid(geom,4326)
4.2 EPSG:4326 (WGS84)转EPSG:3857 (Pseudo-Mercator)
st_transform(geom,3857)
4.3 查询SRID以及用json格式查看地图数据
st_srid(geom)
st_astext(geom)
4.4 ST_GeomFromText 方法(根据字符串构造几何)
st_geomfromtext(WKT,SRID)
select st_geomfromtext('POINT(113.349634 23.139682)',4326)
输出:0101000020E610000075E4486760565C4002D71533C2233740
不指定SRID值则默认为0:
st_geomfromtext('POINT(113.349634 23.139682)')
4.5 ST_AsGeoJSON函数(空间对象输出为JSON字符串)
select st_asgeojson('0101000020E610000075E4486760565C4002D71533C2233740')
输出:{"type":"Point","coordinates":[113.349634,23.139682]}
注:
WTK是坐标,SRID空缺为0
-
POINT:点
-
MULTIPOINT:多点
-
LINE:线
-
POLYLINE:折线
-
EXTENT:矩形
-
CIRCLE:圆
-
POLYGON:多边形
5 三大坐标系转换
坐标系转换库:https://www.npmjs.com/package/coordinate-convert
var coord = CoordinateConvert.wgc2gcj(116.3997, 39.9158)
5.1 经纬度转坐标geographic-coordinate-converter
https://www.npmjs.com/package/geographic-coordinate-converter
import { CoordinateConverter } from "coordinate-converter";
CoordinateConverter.fromDecimal([-36.01011, -2.34856])
.toDegreeMinutes() //"36º 00.607' S 002º 20.914' W"
CoordinateConverter.fromDegreeMinutes("36º 00.607' S 002º 20.914' W")
.toDegreeMinutesSeconds() //"36º 00' 36.4'' S 002º 20' 54.8'' W"
CoordinateConverter.fromDegreeMinutesSeconds("36º 00' 36.4'' S 002º 20' 54.8'' W")
.toDecimal() //"-36.01011 -2.34856"
CoordinateConverter.fromDegreeMinutes("36º 00.607' S 002º 20.914' W")
.toDecimalArray() //[-36.01012, -2.34857]
经纬度转坐标轻量库:https://www.npmjs.com/package/coordinates-converter
const coordWithSymbols = new Coordinate('19°25\'57.3"N 99°07\'59.5"W')
const coordWithSpaces = new Coordinate('19 25 57.3 N 99 07 59.5 W')
coordWithSpaces.toGeoJson() // [-99.133194, 19.432583]
5.2 百度高德地图地图数据转GeoJSON
高德地图数据坐标点一般格式为{P,Q,lng,lat}对象。需要手工吧lng lat转为GeoJSON数组,geojson库提供了方法
// 样例代码 https://lbs.amap.com/api/javascript-api/example/line/obj3d-thinline
var opts = {
subdistrict: 1,
extensions: 'all',
level: 'province'
}
var district = new AMap.DistrictSearch(opts)
district.search('广东省', function (status, result) {
console.log(JSON.stringify(result))
var boundaries = result.districtList[0].boundaries
console.log(JSON.stringify(boundaries))
})
// [[{"P":39.032683,"Q":118.61805600000002,"lng":118.618056,"lat":39.032683},{"P":39.032682,"Q":118.61749199999997,"lng":118.617492,"lat":39.032682},
https://www.npmjs.com/package/geojson 方法
var GeoJSON = require('geojson')
var data = [{name: 'Location A', category: 'Store', street: 'Market', lat: 39.984, lng: -75.343}]
var data2 = { name: 'Location A', category: 'Store', street: 'Market', lat: 39.984, lng: -75.343 }
GeoJSON.parse(data, {Point: ['lat', 'lng']})
GeoJSON.parse(data2, {Point: ['lat', 'lng'], include: ['name']})
var data3 = [
{
x: 0.5,
y: 102.0,
prop0: 'value0'
},
{
line: [[102.0, 0.0], [103.0, 1.0], [104.0, 0.0], [105.0, 1.0]],
prop0: 'value0',
prop1: 0.0
},
{
polygon: [
[ [100.0, 0.0], [101.0, 0.0], [101.0, 1.0], [100.0, 1.0], [100.0, 0.0] ]
],
prop0: 'value0',
prop1: {"this": "that"}
}
]
GeoJSON.parse(data3, {'Point': ['x', 'y'], 'LineString': 'line', 'Polygon': 'polygon'});
6. 常用坐标系统在软件中的判别与操作
6.1 判别(具体问题具体分析)
- 如果数据有坐标系统的定义,则可以从数据的坐标系统中得知坐标系(假如定义的正确)。
- 如果数据没有坐标系统定义,需要通过观察数据坐标值来判断GCS、PCS类型,则需要一定的经验。
- 如果数据是两位数+三位数或者三位数+三位数等落于我国经纬度范围的数字,则可以大致判断是地理坐标系统,只需询问数据提供者,然后自己为数据定义地理坐标系统即可。
- 如果给的数据尺度很小,例如是一个厂房,而且一个单位数值差不多就是1米,则判断是CAD绘图,是未经校准的平面直角坐标系,可以理解为投影坐标系,只不过位置并不准确罢了,需要校准。
- 如果给的数据单位很大,通常是几万、几十万(5位数+6位数,是无投影带的,5位数是经线x方向,6位数是纬线y方向)(6位数+7位数,是有投影带的,6位数是纬线y方向,7位数是经线x方向,通过7位数的前两个数字判断投影带),此时可以粗略判断是投影坐标系统。
- 如果均不是以上的数值,则判断为误操作,可能是错误定义了坐标系,也可能是错误进行投影计算。
7 GIS坐标转换器
一款功能强大、界面简洁、操作简单的GIS格式及坐标系的转换工具。
支持DWG、SHP、MDB、Kml、Kmz、Gpx、GeoJson、EXCEL、TXT、CSV、SQL Server、MySQL、PostgreSQL、JPG、PDF、GeoTiff、Image(img)、Bitmap(bmp)、Png格式和国家2000、西安80、北京54、WGS84、火星坐标、百度坐标、墨卡托坐标的转换,支持批量转换、图层合并和地图数据浏览。
软件官网:www.geosaas.com
8 Java实现CGS2000大地坐标和WGS84经纬度坐标互转
8.1 WGS84转CGS2000
中央子午线需要根据实际设置,参数为经度,纬度,输出值为经度(x),纬度(y)
public static Point WGS84ToCGS2000(double longitude, double latitude)//参数 经度,纬度
{
Point pt = null;
double[] output = new double[2];
double longitude1,latitude1, longitude0, X0,Y0, xval,yval;
//NN曲率半径,测量学里面用N表示
//M为子午线弧长,测量学里用大X表示
//fai为底点纬度,由子午弧长反算公式得到,测量学里用Bf表示
//R为底点所对的曲率半径,测量学里用Nf表示
double a,f, e2,ee, NN, T,C,A, M, iPI;
iPI = 0.0174532925199433; //3.1415926535898/180.0;
a=6378137.0; f=1/298.257222101; //CGCS2000坐标系参数
//a=6378137.0; f=1/298.2572236; //wgs84坐标系参数
longitude0 = 117;//中央子午线 根据实际进行配置
longitude0 = longitude0 * iPI ;//中央子午线转换为弧度
longitude1 = longitude * iPI ; //经度转换为弧度
latitude1 = latitude * iPI ; //纬度转换为弧度
e2=2*f-f*f;
ee=e2*(1.0-e2);
NN=a/Math.sqrt(1.0-e2*Math.sin(latitude1)*Math.sin(latitude1));
T=Math.tan(latitude1)*Math.tan(latitude1);
C=ee*Math.cos(latitude1)*Math.cos(latitude1);
A=(longitude1-longitude0)*Math.cos(latitude1);
M=a*((1-e2/4-3*e2*e2/64-5*e2*e2*e2/256)*latitude1-(3*e2/8+3*e2*e2/32+45*e2*e2
*e2/1024)*Math.sin(2*latitude1)
+(15*e2*e2/256+45*e2*e2*e2/1024)*Math.sin(4*latitude1)-(35*e2*e2*e2/3072)*Math.sin(6*latitude1));
xval = NN*(A+(1-T+C)*A*A*A/6+(5-18*T+T*T+72*C-58*ee)*A*A*A*A*A/120);
yval = M+NN*Math.tan(latitude1)*(A*A/2+(5-T+9*C+4*C*C)*A*A*A*A/24
+(61-58*T+T*T+600*C-330*ee)*A*A*A*A*A*A/720);
X0 = 500000L;
Y0 = 0;
xval = xval+X0; yval = yval+Y0;
//转换为投影
output[0] = xval;
output[1] = yval;
pt = new Point(output[0],output[1]);
return pt;
}
8.2 CGS2000转WGS84
中央子午线需根据实际设置,输入参数为纬度,经度,输出result的顺序为result[0]纬度(y),result[1]经度(x)
private static double formatby6(double num) {
String result = String.format("%.6f", num);
return Double.valueOf(result);
}
//2000转84
public static Point CGS2000ToWGS84(double X, double Y) {
Point pt = null;
double L0 = 117;//中央子午线需根据实际情况设置
double lat ,lon;
Y-=500000;
double [] result = new double[2];
double iPI = 0.0174532925199433;//pi/180
double a = 6378137.0; //长半轴 m
double b = 6356752.31414; //短半轴 m
double f = 1/298.257222101;//扁率 a-b/a
double e = 0.0818191910428; //第一偏心率 Math.sqrt(5)
double ee = Math.sqrt(a*a-b*b)/b; //第二偏心率
double bf = 0; //底点纬度
double a0 = 1+(3*e*e/4) + (45*e*e*e*e/64) + (175*e*e*e*e*e*e/256) + (11025*e*e*e*e*e*e*e*e/16384) + (43659*e*e*e*e*e*e*e*e*e*e/65536);
double b0 = X/(a*(1-e*e)*a0);
double c1 = 3*e*e/8 +3*e*e*e*e/16 + 213*e*e*e*e*e*e/2048 + 255*e*e*e*e*e*e*e*e/4096;
double c2 = 21*e*e*e*e/256 + 21*e*e*e*e*e*e/256 + 533*e*e*e*e*e*e*e*e/8192;
double c3 = 151*e*e*e*e*e*e*e*e/6144 + 151*e*e*e*e*e*e*e*e/4096;
double c4 = 1097*e*e*e*e*e*e*e*e/131072;
bf = b0 + c1*Math.sin(2*b0) + c2*Math.sin(4*b0) +c3*Math.sin(6*b0) + c4*Math.sin(8*b0); // bf =b0+c1*sin2b0 + c2*sin4b0 + c3*sin6b0 +c4*sin8b0 +...
double tf = Math.tan(bf);
double n2 = ee*ee*Math.cos(bf)*Math.cos(bf); //第二偏心率平方成bf余弦平方
double c = a*a/b;
double v=Math.sqrt(1+ ee*ee*Math.cos(bf)*Math.cos(bf));
double mf = c/(v*v*v); //子午圈半径
double nf = c/v;//卯酉圈半径
//纬度计算
lat=bf-(tf/(2*mf)*Y)*(Y/nf) * (1-1/12*(5+3*tf*tf+n2-9*n2*tf*tf)*(Y*Y/(nf*nf))+1/360*(61+90*tf*tf+45*tf*tf*tf*tf)*(Y*Y*Y*Y/(nf*nf*nf*nf)));
//经度偏差
lon=1/(nf*Math.cos(bf))*Y -(1/(6*nf*nf*nf*Math.cos(bf)))*(1+2*tf*tf +n2)*Y*Y*Y + (1/(120*nf*nf*nf*nf*nf*Math.cos(bf)))*(5+28*tf*tf+24*tf*tf*tf*tf)*Y*Y*Y*Y*Y;
result[0] =formatby6(lat/iPI);
result[1] =formatby6(L0+lon/iPI);
//System.out.println(result[1]+","+result[0]);
pt = new Point(result[1],result[0]);
return pt;
}
参考
文章出处登录后可见!