本身线性判别分析是包含在西瓜书第三章的,这一章主讲的是线性模型
在问题开始之前先要搞清楚几个问题,什么是线性模型,线性模型是干什么的,什么是线性判别分析,线性判别分析又是干什么的。
先理解一句话:
LDA是监督学习的降维技术。
监督学习和无监督学习:
- 输入的训练数据都有标签,则为有监督学习
- 如果数据没有标签,则是无监督学习,也即聚类(clustering)
降维技术:
- 降低数据的维数,将原始高维特征空间中的点向一个低维空间投影,新的空间维度低于原始特征空间,所以维数减少了
- 降维在一定的信息损失范围内,可以为我们节省大量的时间和成本
说到LDA,就要提到PCA
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。
PCA是不考虑样本类别输出的无监督降维技术,他俩正好相反。
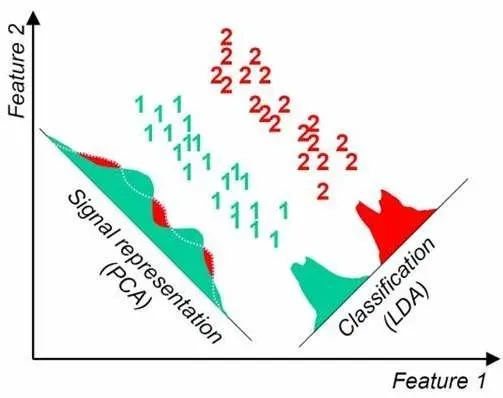
LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。
如下图所示。 我们要将数据在低维度上进行投影;投影后希望同种类别数据的投影点尽可能的接近,不同类别的数据的类别中心之间的距离尽可能的远。
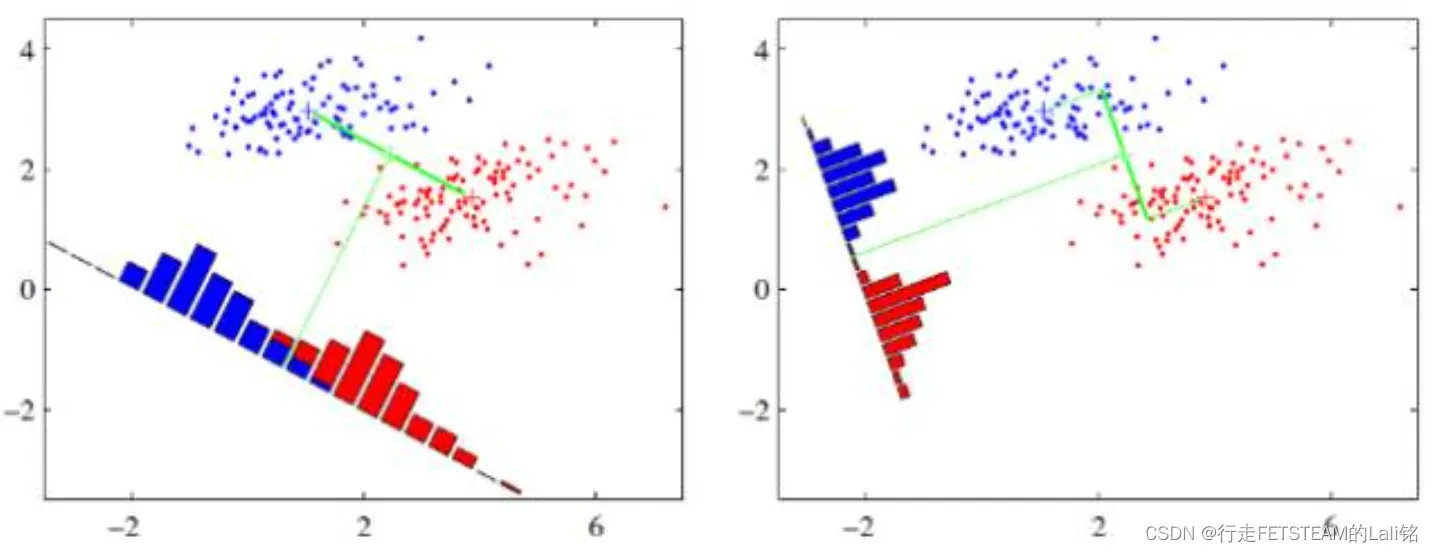
上图例举两种投影方式:哪一种能更好的满足我们的标准呢?
答案:右图要比左图的投影效果好
蓝色和红色各代表同一类数据:右图的蓝红数据分布集中,类间的距离明显。左图边界处数据混杂,故效果差于右图。这就是LDA的主要思想。
当然在实际应用中,数据是多个类别的,我们的原始数据一般也是超过二维的,投影后的也一般不是直线,而是一个低维的超平面。
已经搞清楚LDA是做什么的又明白了LDA的思想,可LDA在数学中怎么去算呢?
接下来通过介绍协方差,协方差矩阵来做铺垫为理解咱们的终极公式做准备。
协方差:
定义:协方差用于衡量两个变量的总体误差,从而描述随机变量的相关性。
通过下面这个例子可以让大家更好理解什么是协方差:
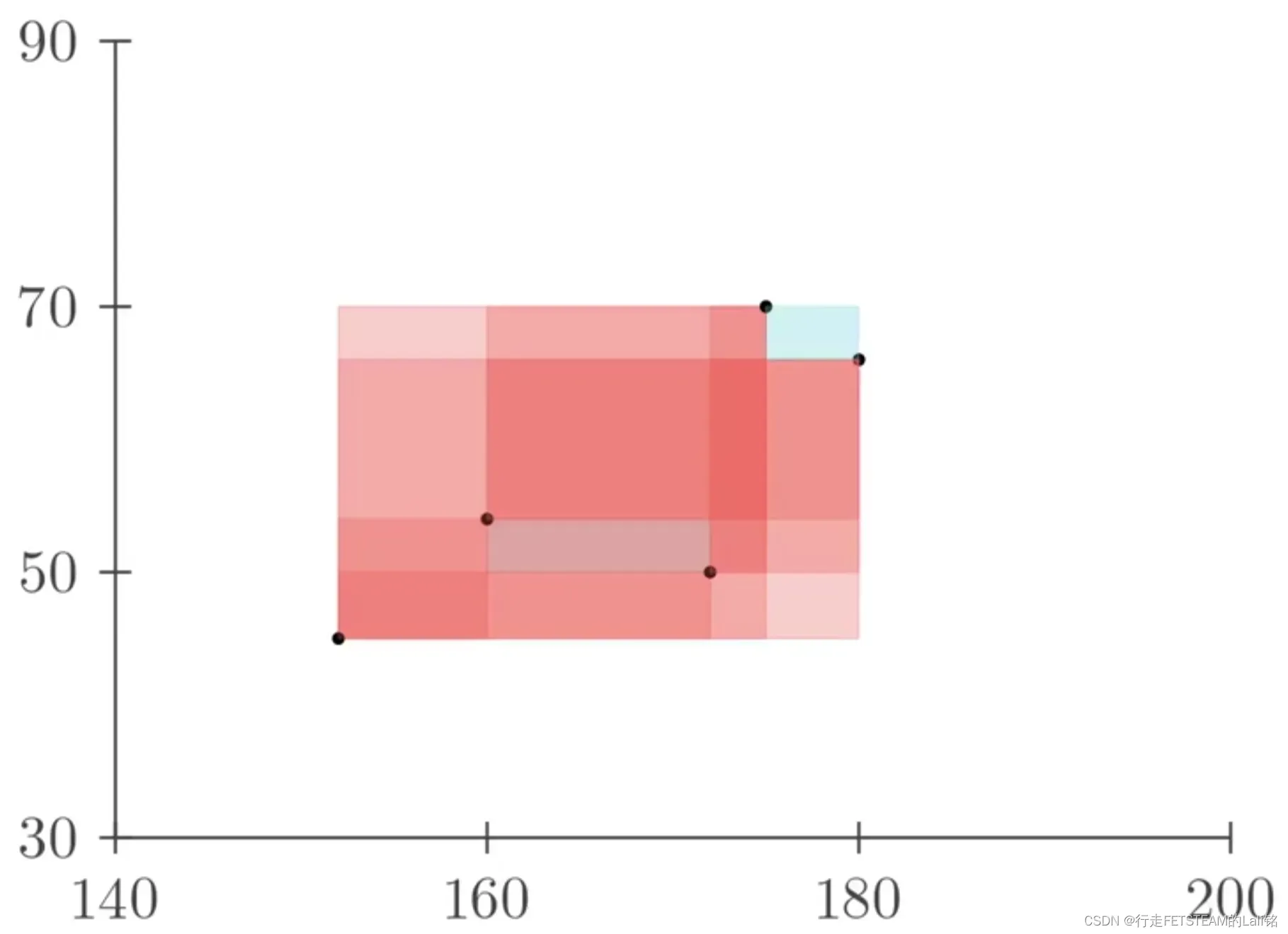

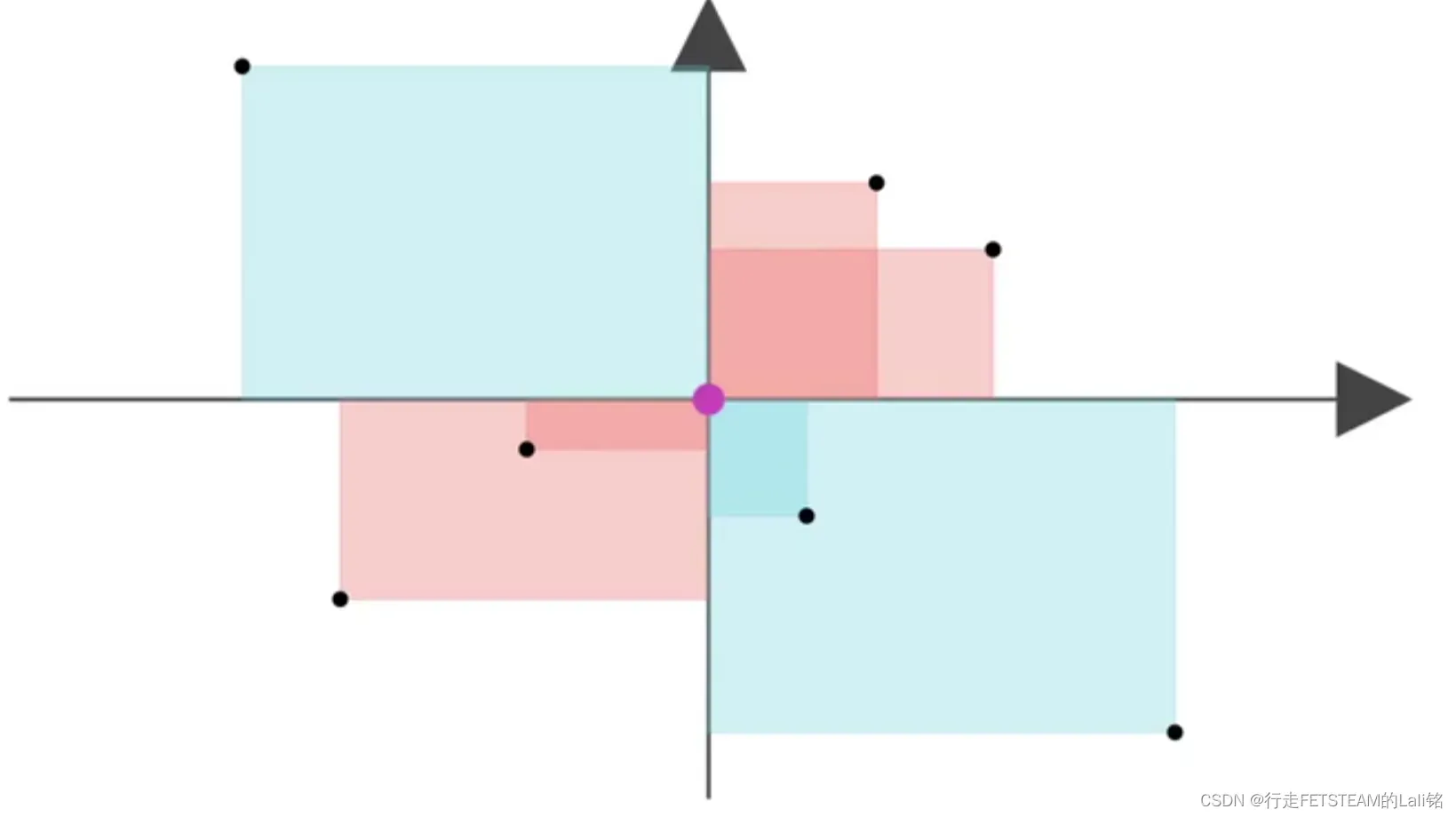
我们把身高体重在坐标系中描点,相对标记点身高增加,体重也增加标记为红色,也就是正相关;相反的,相对标记点身高和体重负相关标记为蓝色。
任意标记点之间全部以矩形连接,全部连接后红色区域远远大于蓝色区域,我们可以认为身高和体重在整体上是正相关的。
因为每新增一个点都要与之前存在的点进行相关性比较,咱们索性简化为和均值比较
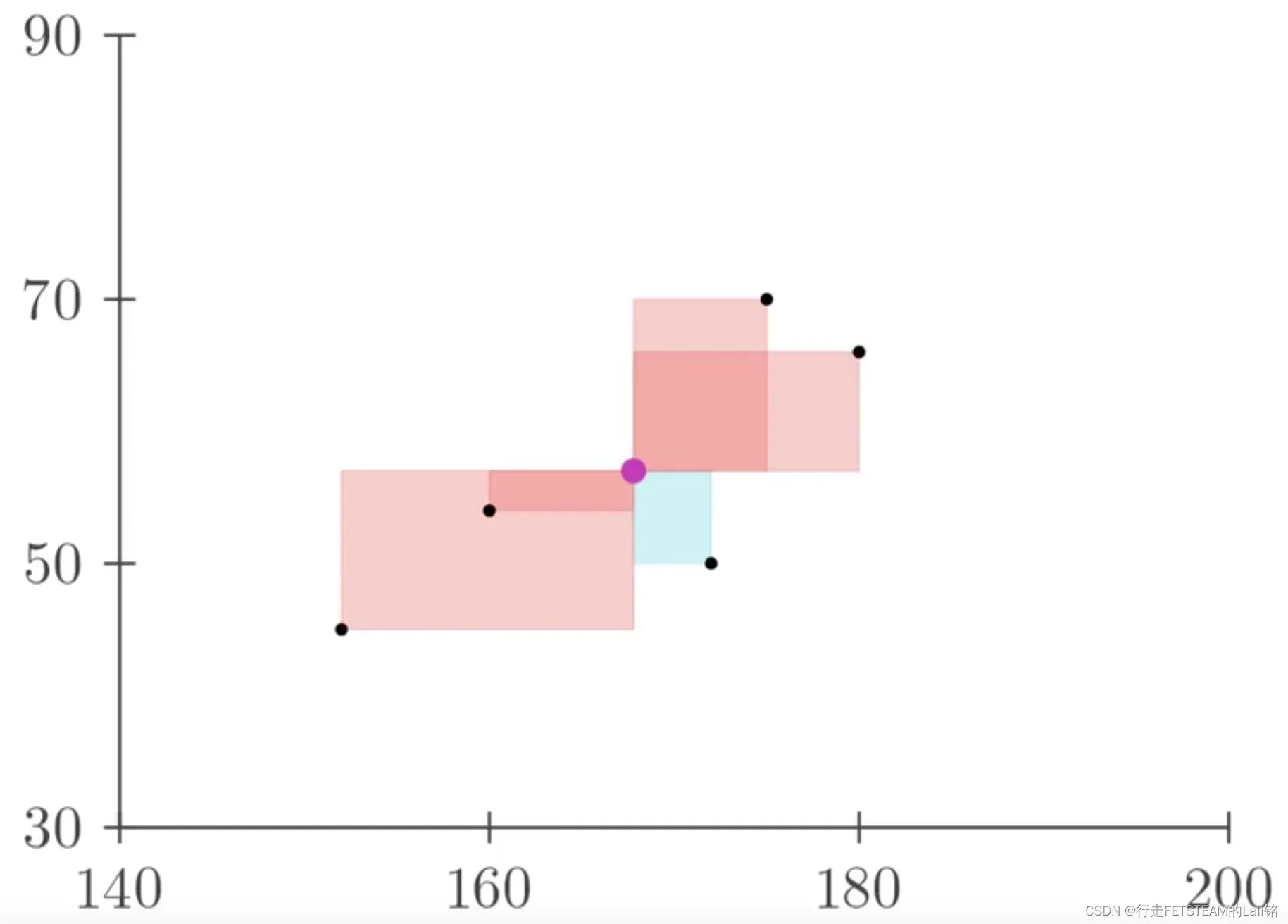

于是便可以通过比较 的大小来其判断相关性了
等等——那如果来了两个不太正常的人类,岂不是会得出违背常理的“身高和体重成负相关”结论
于是我们再引入概率,底部的平均改为加权平均。
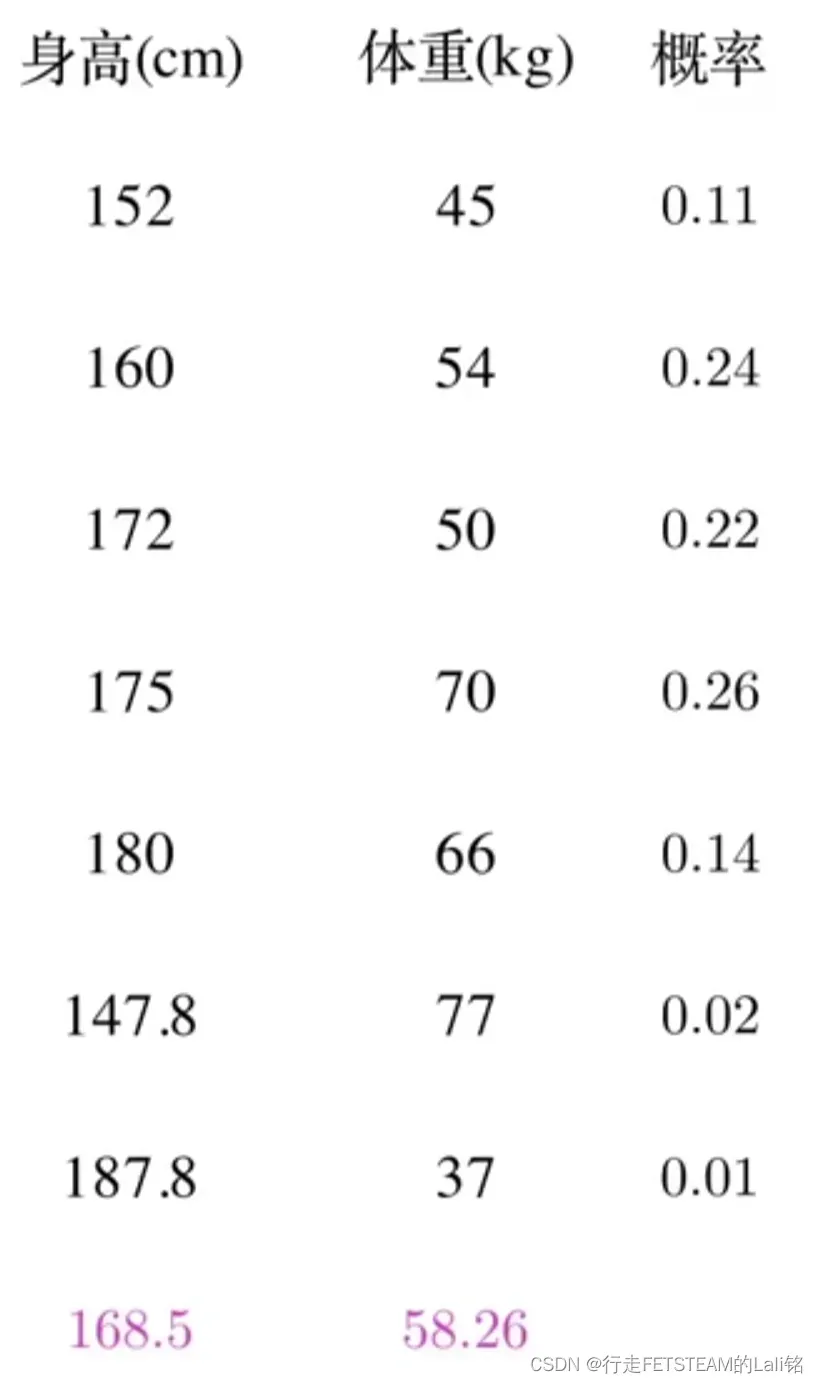
最后可以得到加权后的图形面积,也就是下图:

这里把 的平均改为加权平均符号,乘上每一项的概率;
得到 。
把这个式子写成期望的形式![]() ,这就是协方差公式。
,这就是协方差公式。
协方差矩阵
在进行多维数据分析时,不同维度之间的相关程度就需要协方差矩阵来描述,维度之间的两两相关程度就构成了协方差矩阵,而协方差矩阵主对角线上的元素即为每个维度上的数据方差。
对于二维的数据,任意两个维度之间求其协方差,我们可以得到这4个协方差(方差可以理解成特殊的协方差),就构成了协方差矩阵。
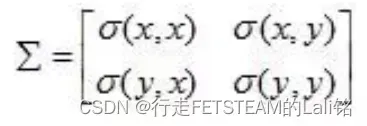
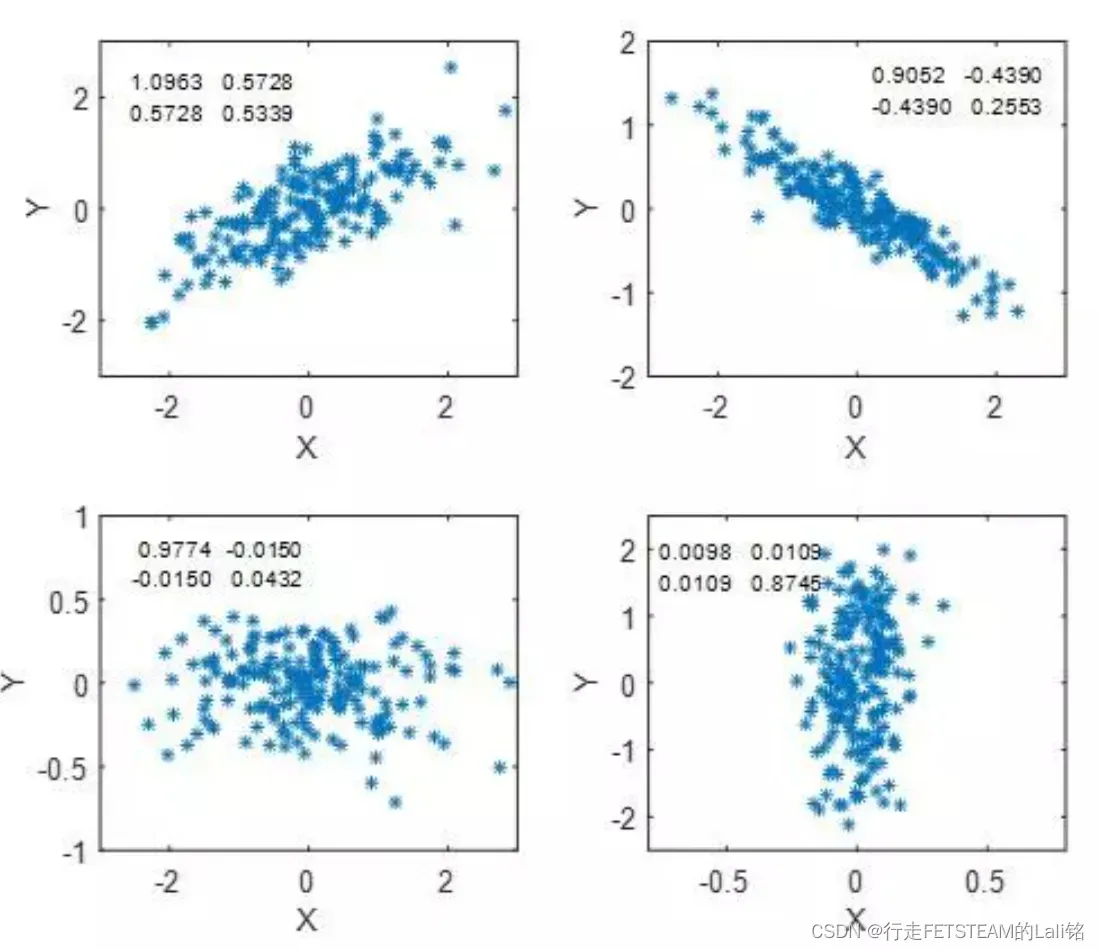
如果说x与y是正相关关系,即y必然随着x的增加而增加,同样x也随着y的增加而增加,即y与x呈正相关关系,所以有,因此协方差矩阵必然是一个实对称矩阵,其主对角线元素为方差,其余为协方差。接下来我们从2维数据分布情况,来看协方差矩阵的几何意义。
从投影下看LDA
因为LDA用到了投影,所以这里有必要科普一下投影的知识。以二维平面为例,如图所示
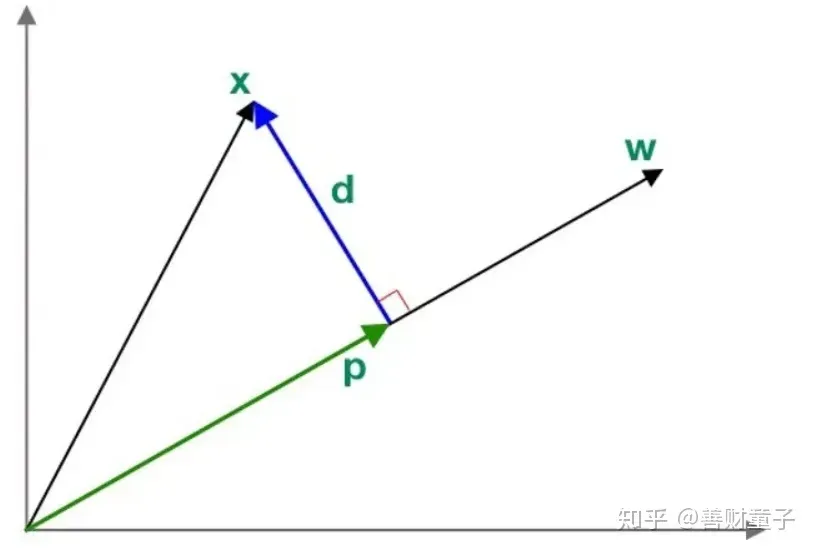
我们要计算向量在
上的投影
,这里
和
成比例关系:
(c是常数)。
- 向量
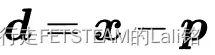 ,
, - d与 p垂直,它们的内积为0,

于是可以推得:

所以,投影 。
文章出处登录后可见!
