线性代数

线性代数主要包含向量、向量空间（或称线性空间）以及向量的线性变换和有限维的线性方程组．

1. 向量和向量空间

1.1 向量

**标量（Scalar）**是一个实数，只有大小，没有方向．标量一般用斜体小写英文字母𝑎, 𝑏, 𝑐来表示．**向量（Vector）**是由一组实数组成的有序数组，同时具有大小和方向．一个𝑁 维向量𝒂是由𝑁 个有序实数组成，表示为

𝒂 = [𝑎1 , 𝑎2 , ⋯ , 𝑎𝑁 ],

其中𝑎𝑛 称为向量𝒂的第𝑛个分量，或第𝑛维．向量符号一般用黑斜体小写英文字母𝒂, 𝒃, 𝒄，或小写希腊字母𝛼, 𝛽, 𝛾等来表示．

1.2 向量空间

向量空间（Vector Space），也称线性空间（Linear Space），是指由向量组成的集合，并满足以下两个条件：

（1） 向量加法+：向量空间𝒱 中的两个向量𝒂和𝒃，它们的和𝒂 + 𝒃也属于

空间𝒱；

（2） 标量乘法⋅：向量空间𝒱 中的任一向量𝒂和任一标量𝑐，它们的乘积𝑐⋅𝒂

也属于空间𝒱．

欧氏空间 一个常用的线性空间是欧氏空间（Euclidean Space）．一个欧氏空间表示通常为ℝ𝑁，其中𝑁 为空间维度（Dimension）．欧氏空间中的向量加法和标量乘法定义为：

[𝑎1 , 𝑎2 , ⋯ , 𝑎𝑁 ] + [𝑏1 , 𝑏2 , ⋯ , 𝑏𝑁 ] = [𝑎1 + 𝑏1 , 𝑎2 + 𝑏2 , ⋯ , 𝑎𝑁 + 𝑏𝑁 ], (A.2)

𝑐 ⋅ [𝑎1 , 𝑎2 , ⋯ , 𝑎𝑁 ] = [𝑐𝑎1 , 𝑐𝑎2 , ⋯ , 𝑐𝑎𝑁 ],

其中𝑎, 𝑏, 𝑐 ∈ ℝ为标量．

线性子空间 向量空间 𝒱 的线性子空间 𝒰 是 𝒱 的一个子集，并且满足向量空间的条件（向量加法和标量乘法）．

线性无关 线性空间 𝒱 中的 𝑀 个向量 {𝒗1 , 𝒗2 , ⋯ , 𝒗𝑀}，如果对任意的一组标量𝜆1 , 𝜆2 , ⋯ , 𝜆𝑀，满足𝜆1𝒗1 + 𝜆2𝒗2 +⋯ + 𝜆𝑀𝒗𝑀 = 0，则必然 𝜆1 = 𝜆2 = ⋯ = 𝜆𝑀 = 0，那么{𝒗1 , 𝒗2 , ⋯ , 𝒗𝑀}是线性无关的，也称为线性独立的．

基向量 𝑁 维向量空间𝒱 的基（Base）ℬ = {𝒆1 , 𝒆2 , ⋯ , 𝒆𝑁 }是𝒱 的有限子集，其元素之间线性无关．向量空间 𝒱 中所有的向量都可以按唯一的方式表达为 ℬ 中向量的线性组合．对任意𝑣 ∈ 𝒱，存在一组标量(𝜆1 , 𝜆2 , ⋯ , 𝜆𝑁 )使得

𝒗 = 𝜆1𝒆1 + 𝜆2𝒆2 + ⋯ + 𝜆𝑁 𝒆𝑁 ,

其中基 ℬ 中的向量称为基向量（Base Vector）．如果基向量是有序的，则标量(𝜆1 , 𝜆2 , ⋯ , 𝜆𝑁 )称为向量𝒗关于基ℬ 的坐标（Coordinate）．𝑁 维空间𝒱 的一组标准基（Standard Basis）为

𝒆1 = [1, 0, 0, ⋯ , 0],

𝒆2 = [0, 1, 0, ⋯ , 0],

⋯

𝒆𝑁 = [0, 0, 0, ⋯ , 1],

𝒱 中的任一向量𝒗 = [𝑣1 , 𝑣2 , ⋯ , 𝑣𝑁 ]可以唯一地表示为

[𝑣1 , 𝑣2 , ⋯ , 𝑣𝑁 ] = 𝑣1𝒆1 + 𝑣2𝒆2 + ⋯ + 𝑣𝑁 𝒆𝑁 ,

𝑣1 , 𝑣2 , ⋯ , 𝑣𝑁 也称为向量𝒗的笛卡尔坐标（Cartesian Coordinate）．向量空间中的每个向量可以看作一个线性空间中的笛卡尔坐标．

内积 一个𝑁 维线性空间中的两个向量𝒂和𝒃，其内积（Inner Product）为

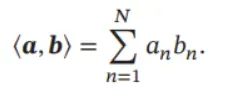
内积也称为点积（Dot Product）或标量积（Scalar Product）．

正交 如果向量空间中两个向量的内积为 0，则它们正交（Orthogonal）．如果向量空间中一个向量𝒗与子空间𝒰 中的每个向量都正交，那么向量𝒗和子空间𝒰正交．

1.3 范数

范数（Norm）是一个表示向量“长度”的函数，为向量空间内的所有向量赋

予非零的正长度或大小．对于一个𝑁 维向量𝒗，一个常见的范数函数为ℓ𝑝 范数，

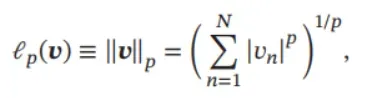
其中𝑝 ≥ 0为一个标量的参数．常用的𝑝的取值有1，2，∞等．

ℓ1 范数 ℓ1 范数为向量的各个元素的绝对值之和．

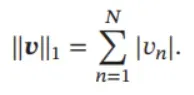
ℓ2 范数 ℓ2 范数为向量的各个元素的平方和再开平方．

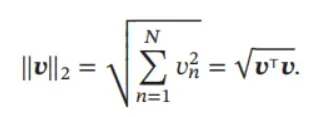
ℓ2 范数又称为Euclidean 范数或者Frobenius 范数．从几何角度，向量也可

以表示为从原点出发的一个带箭头的有向线段，其ℓ2 范数为线段的长度，也常称为向量的模．

ℓ∞ 范数 ℓ∞ 范数为向量的各个元素的最大绝对值，

‖𝒗‖∞ = max{𝑣1 , 𝑣2 , ⋯ , 𝑣𝑁 }.

图A.1给出了常见范数的示例，其中红线表示不同范数的ℓ𝑝 = 1的点．

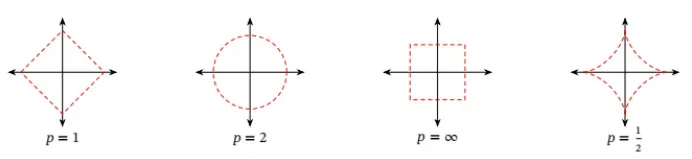
图 A.1 常见的范数

1.4 常见的向量

全 0 向量指所有元素都为 0 的向量，用 0 表示．全 0 向量为笛卡尔坐标系中的原点．

全1向量指所有元素都为1的向量，用1表示．

one-hot 向量为有且只有一个元素为 1，其余元素都为 0 的向量．one-hot 向量是在数字电路中的一种状态编码，指对任意给定的状态，状态寄存器中只有1位为1，其余位都为0．

2. 矩阵

2.1 线性映射

线性映射（Linear Mapping） 是指从线性空间𝒳 到线性空间𝒴 的一个映射

函数𝑓 ∶ 𝒳 → 𝒴，并满足：对于𝒳 中任何两个向量𝒖和𝒗以及任何标量𝑐，有

𝑓(𝒖 + 𝒗) = 𝑓(𝒖) + 𝑓(𝒗),

𝑓(𝑐𝒗) = 𝑐𝑓(𝒗).

两个有限维欧氏空间的映射函数𝑓 ∶ ℝ𝑁 → ℝ𝑀 可以表示为

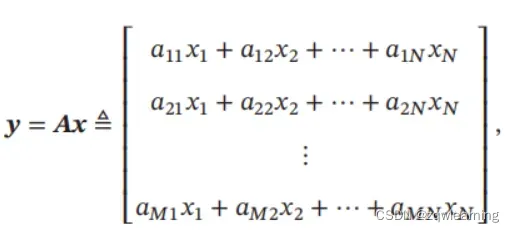
其中 𝑨 是一个由 𝑀 行 𝑁 列个元素排列成的矩形阵列，称为 𝑀 × 𝑁 的矩阵（Matrix）：

向量 𝒙 ∈ ℝ𝑁 和 𝒚 ∈ ℝ𝑀 为两个空间中的向量．𝒙 和 𝒚 可以分别表示为 𝑁 × 1 的矩阵和𝑀 × 1的矩阵：

这种表示形式称为列向量，即只有一列的矩阵．

为简化书写、方便排版起见，本书约定行向量（即 1 × 𝑁 的矩阵）用逗号隔离的向量[𝑥1 , 𝑥2 , ⋯ , 𝑥𝑁 ]表示；列向量用分号隔开的向量𝒙 = [𝑥1; 𝑥2; ⋯ ; 𝑥𝑁 ]表 示，或用行向量的转置[𝑥1, 𝑥2 , ⋯ , 𝑥𝑁 ]T 表示．

矩阵𝑨 ∈ ℝ𝑀×𝑁 定义了一个从空间ℝ𝑁 到空间ℝ𝑀 的线性映射．一个矩阵𝑨从左上角数起的第𝑚行第𝑛列上的元素称为第𝑚, 𝑛项，通常记为[𝑨]𝑚𝑛 或𝑎𝑚𝑛．

2.2 仿射变换

仿射变换（Affine Transformation）是指通过一个线性变换和一个平移，将一个向量空间变换成另一个向量空间的过程． 令𝑨 ∈ ℝ𝑁×𝑁 为𝑁 × 𝑁 的实数矩阵，𝒙 ∈ ℝ𝑁 是𝑁 维向量空间中的点，仿射变换可以表示为

𝒚 = 𝑨𝒙 + 𝒃,

其中𝒃 ∈ ℝ𝑁 为平移项．当𝒃 = 0时，仿射变换就退化为线性变换．

仿射变换可以实现线性空间中的旋转、平移、缩放变换．仿射变换不改变原始空间的相对位置关系，具有以下性质．1）共线性（Collinearity）不变：在同一条直线上的三个或三个以上的点，在变换后依然在一条直线上；2）比例不变：不同点之间的距离比例在变换后不变；3）平行性不变：两条平行线在转换后依然平行；4）凸性不变：一个凸集（Convex Set）在转换后依然是凸的．

2.3 矩阵操作

加 如果𝑨和𝑩 都为𝑀 × 𝑁 的矩阵，则𝑨和𝑩 的加也是𝑀 × 𝑁 的矩阵，其每个元素是A和B相应元素相加，即

[𝑨 + 𝑩]𝑚𝑛 = 𝑎𝑚𝑛 + 𝑏𝑚𝑛.

乘积 假设有两个矩阵 𝑨 和 𝑩 分别表示两个线性映射 𝑔 ∶ ℝ𝐾 → ℝ𝑀 和 𝑓 ∶ℝ𝑁 → ℝ𝐾，则其复合线性映射

(𝑔 ∘ 𝑓)(𝒙) = 𝑔(𝑓(𝒙)) = 𝑔(𝑩𝒙) = 𝑨(𝑩𝒙) = (𝑨𝑩)𝒙,

其中𝑨𝑩 表示矩阵𝑨和𝑩 的乘积，定义为

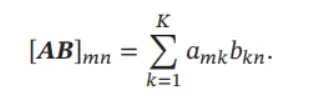
两个矩阵的乘积仅当第一个矩阵的列数和第二个矩阵的行数相等时才能定义如𝑨是𝑀 × 𝐾 矩阵和𝑩 是𝐾 × 𝑁 矩阵，则乘积𝑨𝑩 是一个𝑀 × 𝑁 的矩阵．

矩阵的乘法满足结合律和分配律：

（1） 结合律：(𝑨𝑩)𝑪 = 𝑨(𝑩𝑪),

（2） 分配律：(𝑨 + 𝑩)𝑪 = 𝑨𝑪 + 𝑩𝑪，𝑪(𝑨 + 𝑩) = 𝑪𝑨 + 𝑪𝑩.

转置 𝑀 × 𝑁 的矩阵𝑨的转置（Transposition）是一个𝑁 × 𝑀 的矩阵，记为𝑨T， 𝑨T 的第𝑚行第𝑛列的元素是原矩阵𝑨的第𝑛行第𝑚列的元素，

[𝑨T]𝑚𝑛 = [𝑨]𝑛𝑚.

Hadamard 积 矩阵 𝑨 和矩阵 𝑩 的Hadamard 积（Hadamard Product）也称为逐点乘积，为𝑨和𝑩 中对应的元素相乘．

[𝑨 ⊙ 𝑩]𝑚𝑛 = 𝑎𝑚𝑛𝑏𝑚𝑛.

一个标量𝑐与矩阵𝑨乘积为𝑨的每个元素是𝑨的相应元素与𝑐的乘积

[𝑐𝑨]𝑚𝑛 = 𝑐𝑎𝑚𝑛.

Kronecker****积 如果𝑨是𝑀×𝑁 的矩阵，𝑩是𝑆×𝑇 的矩阵，那么它们的Kronecker积（Kronecker Product）是一个𝑀𝑆 × 𝑁𝑇 的矩阵：

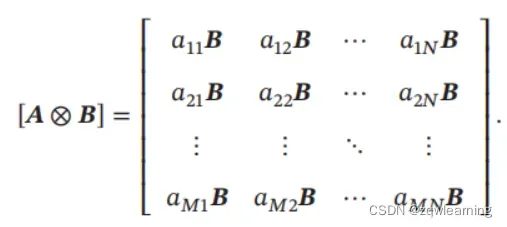
外积 两个向量 𝒂 ∈ ℝ𝑀 和 𝒃 ∈ ℝ𝑁 的外积（Outer Product）是一个 𝑀 × 𝑁 的矩阵，定义为

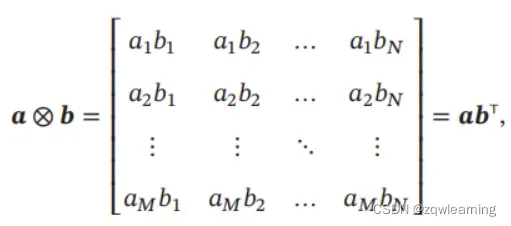
其中[𝒂 ⊗ 𝒃]𝑚𝑛 = 𝑎𝑚𝑏𝑛．

向量化 矩阵的向量化（Vectorization）是将矩阵表示为一个列向量．令 𝑨 =[𝑎𝑖𝑗]𝑀×𝑁，向量化算子vec(⋅)定义为

vec(𝑨) = [𝑎11, 𝑎21, ⋯ , 𝑎𝑀1, 𝑎12, 𝑎22, ⋯ , 𝑎𝑀2, ⋯ , 𝑎1𝑁 , 𝑎2𝑁 , ⋯ , 𝑎𝑀𝑁 ]T.

迹 方块矩阵 𝑨 的对角线元素之和称为它的迹（Trace），记为 𝑡𝑟(𝑨)．尽管矩阵的乘法不满足交换律，但它们的迹相同，即𝑡𝑟(𝑨𝑩) = 𝑡𝑟(𝑩𝑨)．

行列式 方块矩阵 𝑨 的行列式是一个将其映射到标量的函数，记作 det(𝑨) 或

|𝑨|．行列式可以看作有向面积或体积的概念在欧氏空间中的推广．在 𝑁 维欧氏空间中，行列式描述的是一个线性变换对“体积”所造成的影响．

一个𝑁 × 𝑁 的方块矩阵𝑨的行列式定义为：

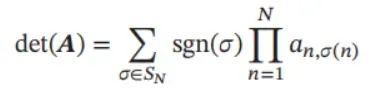
其中 𝑆𝑁 是 {1, 2, ⋯ , 𝑁} 的所有排列的集合，𝜎 是其中一个排列，𝜎(𝑛) 是元素 𝑛 在排列𝜎中的位置，sgn(𝜎)表示排列𝜎的符号差，定义为

其中逆序对的定义为：在排列 𝜎 中，如果有序数对 (𝑖, 𝑗) 满足 1 ≤ 𝑖 < 𝑗 ≤ 𝑁 但𝜎(𝑖) > 𝜎(𝑗)，则其为𝜎的一个逆序对．

秩 一个矩阵 𝑨 的列秩是 𝑨 的线性无关的列向量数量，行秩是 𝑨 的线性无关的行向量数量．一个矩阵的列秩和行秩总是相等的，简称为秩（Rank）．一个𝑀 × 𝑁 的矩阵𝑨的秩最大为min(𝑀, 𝑁)．若rank(𝑨) = min(𝑀, 𝑁)，则称矩阵为满秩的．如果一个矩阵不满秩，说明其包含线性相关的列向量或行向量，其行列式为0．

两个矩阵的乘积𝑨𝑩 的秩rank(𝑨𝑩) ≤ min ( rank(𝑨),rank(𝑩))．

范数 矩阵的范数有很多种形式，其中常用的ℓ𝑝 范数定义为

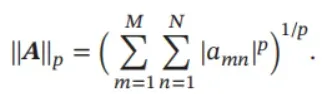
2.4 矩阵类型

对称矩阵 对称矩阵（Symmetric Matrix）指其转置等于自己的矩阵，即满足𝑨 = 𝑨T．

对角矩阵 对角矩阵（Diagonal Matrix）是一个主对角线之外的元素皆为 0 的矩阵．一个对角矩阵𝑨满足

[𝑨]𝑚𝑛 = 0 ∀𝑚, 𝑛 ∈ {1, ⋯ , 𝑁}, and 𝑚 ≠ 𝑛.

对角矩阵通常指方块矩阵，但有时也指矩形对角矩阵（Rectangular Diagonal Matrix），即一个𝑀 × 𝑁 的矩阵，其除𝑎𝑖𝑖 之外的元素都为0．一个𝑁 × 𝑁 的对角矩阵𝑨也可以记为diag(𝒂)，𝒂为一个𝑁 维向量，并满足

[𝑨]𝑛𝑛 = 𝑎𝑛.

𝑁 × 𝑁 的对角矩阵𝑨 = diag(𝒂)和𝑁 维向量𝒃的乘积为一个𝑁 维向量

𝑨𝒃 = diag(𝒂)𝒃 = 𝒂 ⊙ 𝒃,

其中⊙表示按元素乘积，即[𝒂 ⊙ 𝒃]𝑛 = 𝑎𝑛𝑏𝑛, 1 ≤ 𝑛 ≤ 𝑁．

单位矩阵 单位矩阵（Identity Matrix）是一种特殊的对角矩阵，其主对角线元素为 1，其余元素为 0．𝑁 阶单位矩阵 𝑰𝑁，是一个 𝑁 × 𝑁 的方块矩阵，可以记为𝐼𝑁 = diag(1, 1, ⋯ , 1)．

一个𝑀 × 𝑁 的矩阵A和单位矩阵的乘积等于其本身，即

𝑨𝑰𝑁 = 𝑰𝑀𝑨 = 𝑨.

逆矩阵 对于一个𝑁 × 𝑁 的方块矩阵𝑨，如果存在另一个方块矩阵𝑩 使得

𝑨𝑩 = 𝑩𝑨 = 𝑰𝑁 ,

其中 𝑰𝑁 为单位阵，则称 𝑨 是可逆的．矩阵 𝑩 称为矩阵 𝑨 的逆矩阵（Inverse Matrix），记为𝑨 −1．

一个方阵的行列式等于0当且仅当该方阵不可逆．

正定矩阵 对于一个 𝑁 × 𝑁 的对称矩阵 𝑨，如果对于所有的非零向量 𝒙 ∈ ℝ𝑁都满足

𝒙T𝑨𝒙 > 0,

则 𝑨 为正定矩阵（Positive-Definite Matrix）．如果 𝒙T𝑨𝒙 ≥ 0，则 𝑨 是半正定矩阵（Positive-Semidefinite Matrix）．

正交矩阵 如果一个𝑁 × 𝑁 的方块矩阵𝑨的逆矩阵等于其转置矩阵，即

𝑨T = 𝑨−1,

则𝑨为正交矩阵（Orthogonal Matrix）．

正交矩阵满足𝑨T𝑨 = 𝑨𝑨T = 𝑰𝑁，即正交矩阵的每一行（列）向量和自身的内积为1，和其他行（列）向量的内积为0．

Gram

矩阵 向量空间中一组向量 𝒂1 , 𝒂2 , ⋯ , 𝒂𝑁 的Gram 矩阵（Gram Matrix） 𝑮 是内积的对称矩阵，其元素[𝑮]𝑚𝑛 = 𝒂T𝑚𝒂𝑛．

2.5 特征值与特征向量

对一个𝑁 × 𝑁 的矩阵𝑨，如果存在一个标量𝜆和一个非零向量𝒗满足

𝑨𝒗 = 𝜆𝒗,

则𝜆和𝒗分别称为矩阵𝑨的特征值（Eigenvalue）和特征向量（Eigenvector）．

当用矩阵 𝑨 对它的特征向量 𝒗 进行线性映射时，得到的新向量只是在 𝒗 的长度上缩放𝜆倍．给定一个矩阵的特征值，其对应的特征向量的数量是无限多的．

令𝒖和𝒗是矩阵𝑨的特征值𝜆对应的特征向量，则𝛼𝒖和𝒖 + 𝒗也是特征值𝜆对应的特征向量．

如果矩阵 𝑨 是一个 𝑁 × 𝑁 的实对称矩阵，则存在实数 𝜆1 , ⋯ , 𝜆𝑁，以及 𝑁个互相正交的单位向量 𝒗1 , ⋯ , 𝒗𝑁，使得 𝒗𝑛 为矩阵 𝑨 的特征值为 𝜆𝑛 的特征向量（1 ≤ 𝑛 ≤ 𝑁）．

2.6 矩阵分解

一个矩阵通常可以用一些比较“简单”的矩阵来表示，称为矩阵分解（Matrix Decomposition, or Matrix Factorization）．

2.6.1 特征分解

一个𝑁 × 𝑁 的方块矩阵𝑨的特征分解（Eigendecomposition）定义为

𝑨 = 𝑸𝚲𝑸−1,

其中 𝑸 为 𝑁 × 𝑁 的方块矩阵，其每一列都为 𝑨 的特征向量，𝚲 为对角矩阵，其每一个对角元素分别为𝑨的一个特征值．

如果𝑨为实对称矩阵，那么其不同特征值对应的特征向量相互正交．𝑨可以被分解为

𝑨 = 𝑸𝚲𝑸T,

其中𝑸 为正交矩阵．

2.6.2 奇异值分解

一个𝑀 × 𝑁 的矩阵𝑨的奇异值分解（Singular Value Decomposition，SVD）

定义为

𝑨 = 𝑼𝚺𝑽 T,

其中𝑼 和𝑽 分别为𝑀 × 𝑀 和𝑁 × 𝑁 的正交矩阵，𝚺为𝑀 × 𝑁 的矩形对角矩阵．𝚺对角线上的元素称为奇异值（Singular Value），一般按从大到小排列．

根据公式(A.42)，𝑨𝑨T = 𝑼𝚺𝑽 T𝑽𝚺𝑼T = 𝑼𝚺2𝑼T，𝑨T𝑨 = 𝑽𝚺𝑼T𝑼𝚺𝑽 T =𝑽𝚺2𝑽 T．因此，𝑼 和𝑽 分别为𝑨𝑨T 和𝑨T𝑨的特征向量，𝑨的非零奇异值为𝑨𝑨T 或 𝑨T𝑨的非零特征值的平方根．

由于一个大小为 𝑀 × 𝑁 的矩阵𝑨可以表示空间ℝ𝑁 到空间ℝ𝑀 的一种线性映射，因此奇异值分解相当于将这个线性映射分解为3个简单操作．1）先使用𝑽在原始空间中进行坐标旋转．2）用𝚺对旋转后的每一维进行缩放．如果𝑀 > 𝑁，则补𝑀 − 𝑁 个0；相反，如果𝑀 < 𝑁，则舍去最后的𝑁 − 𝑀 维．3）使用𝑼 进行再一次的坐标旋转．

令𝐾 为矩阵𝑨的非零奇异值的数量，矩阵𝑨可以写为

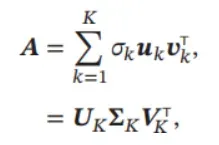
其中 𝑼𝐾 = [𝒖1 , ⋯ , 𝒖𝐾] 和 𝑽𝐾 = [𝒗1 , ⋯ , 𝒗𝐾] 分别为 𝑀 × 𝐾 和 𝑁 × 𝐾 的矩阵， 𝚺𝐾 = diag(𝜎1 , ⋯ , 𝜎𝐾) 为 𝐾 × 𝐾 的对角矩阵．公式(A.44)也称为紧凑的奇异值分解（Compact SVD）．如果令𝐾 < 𝑟𝑎𝑛𝑘(𝑨)，并舍去小的奇异值，则公式(A.44)也称为截断的奇异值分解（Truncated SVD）．在实际应用中，通常使用截断的奇异值分解来提高计算效率，但是截断的奇异值分解只是一种近似的矩阵分解，不能精确重构出原始矩阵．