目录
opencv生成最小外接矩形:
cnt = np.array([[x1,y1],[x2,y2],[x3,y3],[x4,y4]]) # 必须是array数组的形式
rect = cv2.minAreaRect(cnt) # 得到最小外接矩形的(中心(x,y), (宽,高), 旋转角度)
box = cv2.cv.BoxPoints(rect) # cv2.boxPoints(rect) for OpenCV 3.x 获取最小外接矩形的4个顶点
box = np.int0(box)
RotatedRect该类表示平面上的旋转矩形,有三个属性:
- 矩形中心点(质心)
- 边长(长和宽)
- 旋转角度
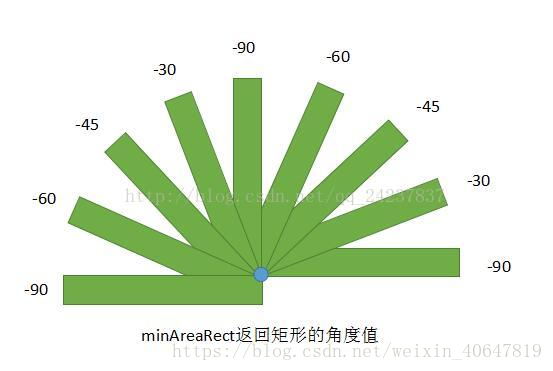
旋转角度angle的范围为[-90,0),当矩形水平或竖直时均返回-90,请看下图:
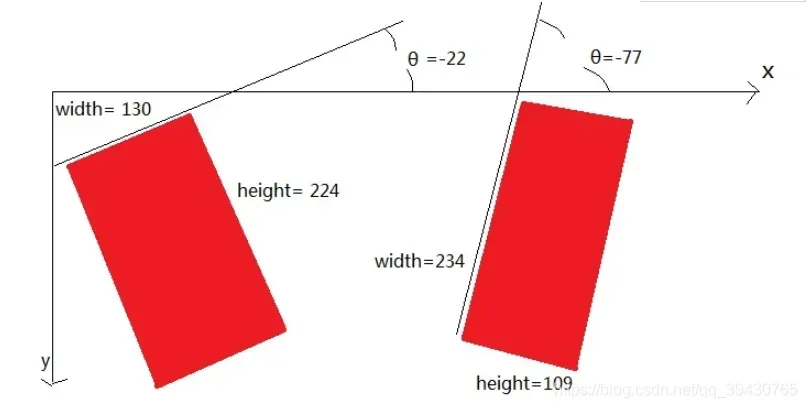
一、组成angel的最小外接矩形的边的选取问题。
angel的形成与选取的最小外接矩形的边有关,在这里我们只给出最终结论,有兴趣的同志,可以自己去验证一下,距离坐标原点最近的最小外接矩形的边,作为angel的一条边或者其延长线,而另一条边为X轴,两条线最终形成一个夹角。如图所示
————————————————
版权声明:本文为CSDN博主「W`Peak」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_39430765/article/details/99431709
最小外接矩形修正版:
GitHub – root12321/Rotation-Detect-yolov5_poly
def cvminAreaRect2longsideformat(x_c, y_c, width, height, theta):
'''
trans minAreaRect(x_c, y_c, width, height, θ) to longside format(x_c, y_c, longside, shortside, θ)
两者区别为:
当opencv表示法中width为最长边时(包括正方形的情况),则两种表示方法一致
当opencv表示法中width不为最长边 ,则最长边表示法的角度要在opencv的Θ基础上-90度
@param x_c: center_x
@param y_c: center_y
@param width: x轴逆时针旋转碰到的第一条边
@param height: 与width不同的边
@param theta: x轴逆时针旋转与width的夹角,由于原点位于图像的左上角,逆时针旋转角度为负 [-90, 0)
@return:
x_c: center_x
y_c: center_y
longside: 最长边
shortside: 最短边
theta_longside: 最长边和x轴逆时针旋转的夹角,逆时针方向角度为负 [-180, 0)
'''
'''
意外情况:(此时要将它们恢复符合规则的opencv形式:wh交换,Θ置为-90)
竖直box:box_width < box_height θ=0
水平box:box_width > box_height θ=0
'''
# print("theta",theta)
theta=int(theta)
if theta == 0:
theta = -90
buffer_width = width
width = height
height = buffer_width
if theta > 0:
if theta != 90: # Θ=90说明wh中有为0的元素,即gt信息不完整,无需提示异常,直接删除
print('θ计算出现异常,当前数据为:%.16f, %.16f, %.16f, %.16f, %.1f;超出opencv表示法的范围:[-90,0)' % (
x_c, y_c, width, height, theta))
return False
if theta < -90:
print(
'θ计算出现异常,当前数据为:%.16f, %.16f, %.16f, %.16f, %.1f;超出opencv表示法的范围:[-90,0)' % (x_c, y_c, width, height, theta))
return False
if width != max(width, height): # 若width不是最长边
longside = height
shortside = width
theta_longside = theta - 90
else: # 若width是最长边(包括正方形的情况)
longside = width
shortside = height
theta_longside = theta
if longside < shortside:
print('旋转框转换表示形式后出现问题:最长边小于短边;[%.16f, %.16f, %.16f, %.16f, %.1f]' % (
x_c, y_c, longside, shortside, theta_longside))
return False
if (theta_longside < -180 or theta_longside >= 0):
print('旋转框转换表示形式时出现问题:θ超出长边表示法的范围:[-180,0);[%.16f, %.16f, %.16f, %.16f, %.1f]' % (
x_c, y_c, longside, shortside, theta_longside))
return False
return x_c, y_c, longside, shortside, theta_longside
def longsideformat2cvminAreaRect(x_c, y_c, longside, shortside, theta_longside):
'''
trans longside format(x_c, y_c, longside, shortside, θ) to minAreaRect(x_c, y_c, width, height, θ)
两者区别为:
当opencv表示法中width为最长边时(包括正方形的情况),则两种表示方法一致
当opencv表示法中width不为最长边 ,则最长边表示法的角度要在opencv的Θ基础上-90度
@param x_c: center_x
@param y_c: center_y
@param longside: 最长边
@param shortside: 最短边
@param theta_longside: 最长边和x轴逆时针旋转的夹角,逆时针方向角度为负 [-180, 0)
@return: ((x_c, y_c),(width, height),Θ)
x_c: center_x
y_c: center_y
width: x轴逆时针旋转碰到的第一条边最长边
height: 与width不同的边
theta: x轴逆时针旋转与width的夹角,由于原点位于图像的左上角,逆时针旋转角度为负 [-90, 0)
'''
theta_longside=int(theta_longside)
if (theta_longside >= -180 and theta_longside < -90): # width is not the longest side
width = shortside
height = longside
theta = theta_longside + 90
else:
width = longside
height = shortside
theta = theta_longside
if theta < -90 or theta >= 0:
print('当前θ=%.1f,超出opencv的θ定义范围[-90, 0)' % theta)
return False
return ((x_c, y_c), (width, height), theta)
def xyxy2xywhn_new(x, w=640, h=640, clip=False, eps=0.0):
# Convert nx4 boxes from [x1, y1, x2, y2] to [x, y, w, h] normalized where xy1=top-left, xy2=bottom-right
if clip:
clip_coords(x, (h - eps, w - eps)) # warning: inplace clip
y = x.clone() if isinstance(x, torch.Tensor) else np.copy(x)
codinate_new=[]
for i in y:
codinate=[]
point=np.array([(i[1],i[2]),(i[3],i[4]),(i[5],i[6]),(i[7],i[8])])
rect = cv2.minAreaRect(point)
c_x = rect[0][0]
c_y = rect[0][1]
w_label = rect[1][0]
h_label = rect[1][1]
theta = rect[-1] # Range for angle is [-90,0)
if(w==0 or h==0 ):
continue
trans_data = cvminAreaRect2longsideformat(c_x, c_y, w_label, h_label, theta)
if not trans_data:
continue
else:
c_x, c_y, longside, shortside, theta_longside = trans_data
theta_label = int(theta_longside + 180.5) # range int[0,180] 四舍五入
if theta_label == 180: # range int[0,179]
theta_label = 179
if theta_label < 0 or theta_label > 179:
# print('id problems,问题出现在该图片中:%s' % (i, img_fullname))
print('出问题的longside形式数据:[%.16f, %.16f, %.16f, %.16f, %.1f]' % (
c_x, c_y, longside, shortside, theta_longside))
continue
codinate.append(i[0])
codinate.append(c_x/w)
codinate.append(c_y/h)
codinate.append(longside/w)
codinate.append(shortside/h)
codinate.append(theta_label)
codinate_new.append(codinate)
codinate_new=np.array(codinate_new)
return codinate_new文章出处登录后可见!
已经登录?立即刷新