Pytorch学习笔记

神经网络训练过程

定义神经网络
迭代输入数据
神经网络计算输出
计算损失
反向传递梯度回到网络的参数
更新网络的权重

卷积层（Convolutional Neural Network,CNN）

卷积神经网络是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于大型图像处理有出色表现。

输入层：在使用卷积神经网络进行图像识别时，输入为进行过转换的图片数据，一张宽为w，高为h，深度为d的图片，表示为hwd。这里，深度为图像存储每个像素所用的位数，比如彩色图像，其一个像素有RGB三个分量，其深度为3。
从数学的角度来看，hwd的图片即为d个hw的矩阵。例如6x16x3的图片，其对应3个6×16的矩阵。在大部分运用中，输入图片的大小h和w，一般是相等的。
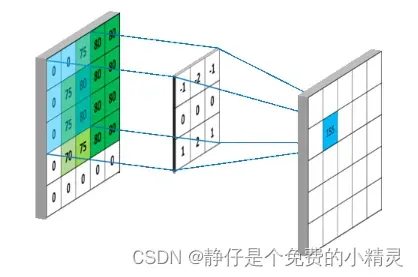
卷积核：
在卷积运算时，会给定一个大小为的方阵，称为过滤器，又叫做卷积核，该矩阵的大小又称为感受野。过滤器的深度d和输入层的深度d维持一致，因此可以得到大小为FFd的过滤器，从数学的角度出发，其为d个FF的矩阵。在实际的操作中，不同的模型会确定不同数量的过滤器，其个数记为K，每一个K包含d个F*F的矩阵，并且计算生成一个输出矩阵。

全连接层

在 CNN 结构中，经多个卷积层和池化层后，连接着1个或1个以上的全连接层．与 MLP 类似，全连接层中的每个神经元与其前一层的所有神经元进行全连接．全连接层可以整合卷积层或者池化层中具有类别区分性的局部信息．为了提升 CNN 网络性能，全连接层每个神经元的激励函数一般采用 ReLU激活函数。
最后一层全连接层的输出值被传递给一个输出，可以采用 softmax 逻辑回归（softmax regression）进行分类，该层也可称为 softmax 层（softmax layer）。对于一个具体的分类任务，选择一个合适的损失函数是十分重要的，CNN 有几种常用的损失函数，各自都有不同的特点。CNN 的全连接层与 MLP 结构一样，CNN 的训练算法也多采用BP算法。

神经网络图像符号表示

n：样本数量
c：图像通道数
w：图像宽度
h：图像高度

1、定义神经网络

以下是定义一个五层的神经网络的代码，第1、2层为卷积层，第3，4，5层为全连接层。

神经网络这一层的输入等于上一层的输入，因此我们在定义神经网络的结构时，需要注意输入输出维度的对应。

我们假设神经网络接收输入数据为 Pytorch学习笔记的矩阵接收输入的格式为[c,h,w]

第一层

定义第一层为卷积层，则输入频道为输入数据的通道数 Pytorch学习笔记，我们定义输出频道为(随便写多大)，卷积核大小为(随便写多大)

第二层

因为第一层的输出频道数为 Pytorch学习笔记，所以定义第二层的输入频道数为，我们定义输出频道为(随便写多大)，卷积核大小为(随便写多大)

第三层

第三层是全连接层，全连接层一般位于整个卷积神经网络的最后，负责将卷积输出的二维特征图转化成一维的一个向量。
全连接层接收的是一个 Pytorch学习笔记维的数据，因此需要将上一层的输出进行转化，我们使用的是pytorch中的view函数。
并且我们还需要计算输入维度，计算方法为：
在第三层中就是
输出维度可以随意定义

第四五层

因为上一层也是全连接层，因此输入维度就是上一层的输出维度

激活函数

Relu激活函数是常用的神经激活函数。
ReLU函数其实是分段线性函数，把所有的负值都变为0，而正值不变，这种操作被成为单侧抑制。
优点：ReLu具有稀疏性，可以使稀疏后的模型能够更好地挖掘相关特征，拟合训练数据

以下是定义神经网络的代码

代码使用jupyter中运行

#定义神经网络
class Net(nn.Module):
    def __init__(self):#定义神经网络结构，输入数据1*32*32[c,h,w]
        super(Net,self).__init__()
        #第一层（卷积层）
        self.conv1 = nn.Conv2d(1,6,3)#定义二维卷积层  输入频道1，输出频道6，卷积3*3
        #第二层（卷积层）
        self.conv2 = nn.Conv2d(6,16,3)#定义二维卷积层  输入频道6，输出频道16，卷积3*3 (卷积)上一层的输出是这一层的输入
        #第三次（全连接层）
        self.fc1 = nn.Linear(16*28*28,512)#输入维度16*（32-2*2）*（32-2*2） = 12544 输出维度512  
        #第四层（全连接层）
        self.fc2 = nn.Linear(512,64)#因为上一层就是全连接层，所以出入维度是上一层的输出维度512，输出维度64
        #第五层（全连接层）
        self.fc3 = nn.Linear(64,2)#输入维度64，输出维度2      
       
    
    def forward(self,x):#定义数据流向
        x = self.conv1(x)#将输入数据传入第一层
        x = F.relu(x)#激活函数，将x的值弄到固定范围内
      
        x = self.conv2(x)#将第一层的输出传到第二层
        x = F.relu(x)#激活
        
        x = x.view(-1,16*28*28)#改变x的形状，把它从16*28*28变成1*12544 
        x = self.fc1(x)#传入全连接层   
        x = F.relu(x)
        
        x = self.fc2(x)
        x = F.relu(x)
        
        x = self.fc3(x)
        
        return x

2、使用神经网络

net = Net()
print(net)

input_data = torch.randn(1,1,32,32)#生成随机输入
print(input_data)
print(input_data.size())#输出：torch.Size([1, 1, 32, 32]) 1：minibatch中有一个数据，大小为1*32*32

# 运行神经网络
out = net(input_data)
print(out)
print(out.size())

#随机生成真实值
target = torch.randn(2)#形状1*2
print(target)
target = target.view(1,-1)#
print(target)
criterion = nn.L1Loss()#定义损失函数
loss = criterion(out,target)#计算损失
print(loss)#真实值和神经网络返回值的误差
#反向传递
net.zero_grad()#清零梯度
loss.backward()#自动清零梯度，反向传递
import torch.optim as optim

optimizer = optim.SGD(net.parameters(),lr =0.01)#更新学习速率0.01
optimizer.step()

out = net(input_data)
print(out)
print(out.size())

loss = criterion(out,target)#计算损失
print(loss)#真实值和神经网络返回值的误差

文章出处登录后可见！

已经登录？立即刷新