一、项目目标
(二)掌握梯度下降法原理;
(三)学会基于矩阵分解的协同过滤算法构建操作系统。
二、实验原理
(一)梯度下降算法的思想原理
本项目使用梯度下降算法目的就是最小化平方差损失函数,通常机器学习都是使用梯度下降的方法来最小化损失函数得到正确的参数。
先任取点(x0,f(x0)),求f(x)在该点x0的导数f′(x0),在用x0减去导数值f′(x0),计算所得就是新的点x1。然后再用x1减去f′(x1)得x2…以此类推,循环多次,慢慢x值就无限接近极小值点。
具体是有公式推导的,不过比较麻烦。其实这个算法是可以直观理解的。比如对于函数f(x)=x ²+y ²,当x大于0时,导数大于零,x减去导数值后变小;只要x大于零,每次减去一个大于零的导数,x值肯定变小。当x小于零时,导数小于零,减去小于零的数后x值增加,所以无论x0起始于何处,最终都能走到极值点0处。只不过有可能从单侧趋近(像走楼梯一样下降),也可能x一会儿大于极值点,一会儿小于极值点,交替地趋近,最终x趋于0。
(二)基于矩阵分解的协同过滤算法原理
将用户喜好矩阵与内容矩阵进行矩阵乘法就能得到用户对物品的预测结果,而我们的目的是预测结果与真实情况越接近越好。所以,我们将预测值与评分表中已评分部分的值构造平方差损失函数为:
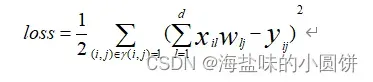
其中:
i:第i个用户
j:第j个物品
d:第d种因素
x:用户喜好矩阵
w:内容矩阵
y:评分矩阵
r:评分记录矩阵,无评分记为0,有评分记为1。r(i,j)=1代表用户i对物品j进行过评分
三、实验及分析
(一)数据集
本实例使用MovieLens 数据集,该数据集(ml latest small)描述了[MovieLens]的五星评级和自由文本标记活动(http://movielens.org),一个电影推荐服务。它包含100836个收视率和3683个标签应用程序,涵盖9742部电影。这些数据由610名用户在1996年3月29日至2018年9月24日期间创建。该数据集于2018年9月26日生成。用户是随机选择的。所有被选中的用户都对至少20部电影进行了评分。不包括人口统计信息。每个用户都由一个id表示,不提供其他信息。
(下载地址:http://files.grouplens.org/datasets/movielens/ml-latest-small.zip,或者https://download.csdn.net/download/smart3s/10946693)中的ratings.csv(用户ID对电影ID的评分)以及movies.csv(电影类别明细)。
(二)数据准备与处理
#读取用户评分矩阵
ratings_df=pd.read_csv(‘E:/ml-latest-small/ratings.csv’)
#读取电影信息矩阵
movies_df=pd.read_csv(‘E:/ml-latest-small/movies.csv’)
#在电影信息矩阵中添加行号(此步非必须,因为直接使用电影id的话
#由于id值过长,会降低算法性能,因此用行号代替)
movies_df[‘movieRow’]=movies_df.index
#筛选movies_df中的特征
movies_df=movies_df[[‘movieRow’,’movieId’,’title’]]
#存储至本地
movies_df.to_csv(‘E:/moviesProcessed.csv’,index=False,header=True,encoding=’utf-8′)
#将ratings_df中的movieId替换为行号
ratings_df=pd.merge(ratings_df,movies_df,on=’movieId’)
ratings_df=ratings_df[[‘userId’,’movieRow’,’rating’]] #筛选ratings_df中的特征
#存储至本地
ratings_df.to_csv(‘E:/ratingsProcessed.csv’,index=False,header=True,encoding=’utf-8′)
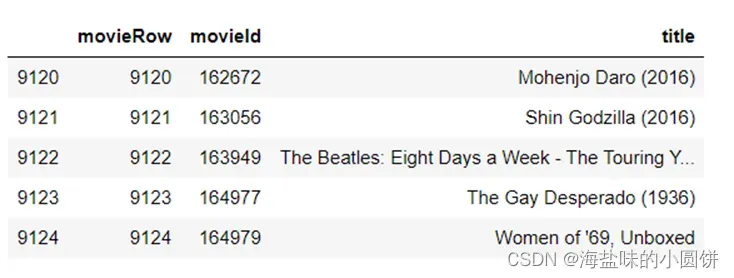
图 1读取电影信息矩阵
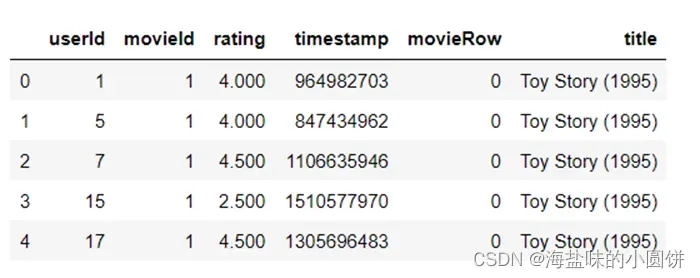
图 2读取用户评分矩阵
(三)创建电影评分矩阵rating和评分记录矩阵record
userNo=ratings_df[‘userId’].max()+1 #用户最大数量,考虑到id可能从0开始,故+1
movieNo=ratings_df[‘movieRow’].max()+1 #电影最大数量,同上
#创建电影评分矩阵矩阵rating
rating=np.zeros((movieNo,userNo))#先创建空矩阵
#进行rating矩阵的填充
flag=0 #记录处理进度
ratings_df_length=np.shape(ratings_df)[0] #ratings_df的样本个数,即行数
for index,row in ratings_df.iterrows():
rating[int(row[‘movieRow’]),int(row[‘userId’])]=row[‘rating’]
flag+=1
print(‘processed %d , %d left’ %(flag,ratings_df_length-flag))
#创建评分记录矩阵record,含有评分记录为1,否则为0
record=rating>0 #出来的是布尔值矩阵
record=np.array(record,dtype=int)#布尔值转整型值

图 3电影评分矩阵rating

图 4评分记录矩阵record
(四)构建模型
def normalizeRatings(rating, record):
m, n =rating.shape
#m代表电影数量,n代表用户数量
rating_mean = np.zeros((m,1))
#每部电影的平均得分
rating_norm = np.zeros((m,n))
#处理过的评分
for i in range(m):
idx = record[i,:] !=0
#每部电影的评分,[i,:]表示每一行的所有列
rating_mean[i] = np.mean(rating[i,idx])
#第i行,评过份idx的用户的平均得分;
#np.mean() 对所有元素求均值
rating_norm[i,idx] -= rating_mean[i]
#rating_norm = 原始得分-平均得分
return rating_norm, rating_mean
rating_norm, rating_mean = normalizeRatings(rating, record)
#因为计算多个0的平均值结果是NAN,所以需要将NAN转成0
rating_norm=np.nan_to_num(rating_norm)
rating_mean=np.nan_to_num(rating_mean)
对电影内容矩阵(特性-物品矩阵)X 和用户喜好矩阵(用户-特性矩阵) θ 的处理:
由于本文并未取得 X 和 θ 的数据,因此采用生成正态随机数的方式
num_features=10 #假设有10种类型的电影
#生成正态随机数,stddev是正态分布的标准差
X_parameters=tf.Variable(tf.random_normal([movieNo,num_features],stddev=0.35))
Theta_parameters=tf.Variable(tf.random_normal([userNo,num_features],stddev=0.35))

图 5将NaNN进行处理后电影评分矩阵
(五)优化算法
optimizer = tf.train.AdamOptimizer(1e-4)
# https://blog.csdn.net/lenbow/article/details/52218551
train = optimizer.minimize(loss)
# Optimizer.minimize对一个损失变量基本上做两件事
# 它计算相对于模型参数的损失梯度。
# 然后应用计算出的梯度来更新变量。
(六)训练模型
# tf.summary的用法 https://www.cnblogs.com/lyc-seu/p/8647792.html
tf.summary.scalar(‘loss’,loss)
#用来显示标量信息
sess = tf.Session()
#https://www.cnblogs.com/wuzhitj/p/6648610.html
init = tf.global_variables_initializer()
sess.run(init)
(七)评估模型
Current_X_parameters, Current_Theta_parameters = sess.run([X_parameters, Theta_parameters])
# Current_X_parameters为用户内容矩阵,Current_Theta_parameters用户喜好矩阵
predicts = np.dot(Current_X_parameters,Current_Theta_parameters.T) + rating_mean
# dot函数是np中的矩阵乘法,np.dot(x,y) 等价于 x.dot(y)
errors = np.sqrt(np.sum((predicts – rating)**2))
# sqrt(arr) ,计算各元素的平方根
errors
四、实验结果
user_id = input(‘您要想哪位用户进行推荐?请输入用户编号:’)
sortedResult = predicts[:, int(user_id)].argsort()[::-1]
# argsort()函数返回的是数组值从小到大的索引值; argsort()[::-1] 返回的是数组值从大到小的索引值
idx = 0
print(‘为该用户推荐的评分最高的20部电影是:’.center(80,’=’))
# center() 返回一个原字符串居中,并使用空格填充至长度 width 的新字符串。默认填充字符为空格。
for i in sortedResult:
print(‘评分: %.2f, 电影名: %s’ % (predicts[i,int(user_id)],movies_df.iloc[i][‘title’]))
# .iloc的用法:https://www.cnblogs.com/harvey888/p/6006200.html
idx += 1
if idx == 20:break
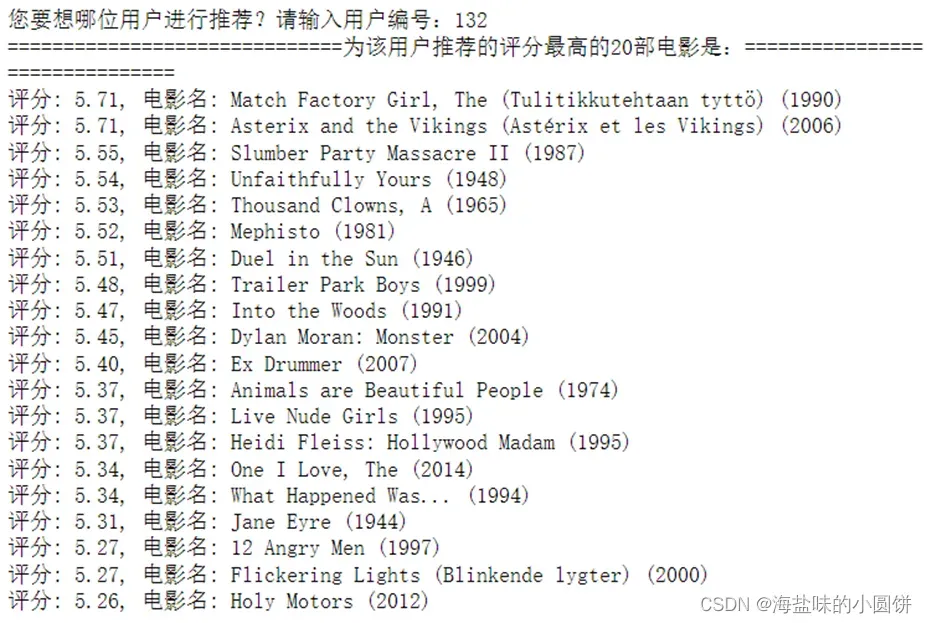
图 6推荐评分最高20部电影
五、总结
由于评分矩阵的稀疏性(因为每一个人只会对少数的物品进行评分),因此传统的矩阵分解技术不能完成矩阵的分解,即使能分解,那样计算复杂度太高,不现实。因此通常的方法是使用已存在评分计算出预测误差(或代价函数),然后使用梯度下降算法调整参数使得误差(代价函数)最小。然后根据头歌平台上的代码基础上进行了一些模型优化,此外,在原本基础上增加了评分,评分可以让用户一目了然来选择自己喜欢的电影。
六、引用
(1)F. Maxwell Harper and Joseph A. Konstan. 2015. The MovieLens Datasets: History and Context. ACM Transactions on Interactive Intelligent Systems (TiiS) 5, 4: 19:1–19:19. The MovieLens Datasets: History and Context: ACM Transactions on Interactive Intelligent Systems: Vol 5, No 4
(2)徐梦锦, 赵晓东. 基于隐语义模型的协同过滤推荐研究[J]. 电脑知识与技术, 2016, 12(7).
(3)Python推荐系统学习笔记(1)基于协同过滤的个性化推荐算法实战—隐语义模型_ZYH@Smart3S的博客-CSDN博客
文章出处登录后可见!
