目的:
关联分析的最终目的,就是为了找出强关联规则
基本概念:
1.支持度(support):
关联规则A->B的支持度support=P(AB),指的是事件A和事件B同时发生的概率(联合概率)
Support(X→Y) = P(X,Y) / P(I) = P(X∩Y) / P(I) = num(X∩Y) / num(I)
2.置信度(confidence):
confidence = P(B|A) = P(AB)/P(A),指的是发生事件A的基础上发生事件B的概率(条件概率)
Confidence(X→Y) = P(Y|X) = P(X,Y) / P(X) = P(X∩Y) / P(X)
3.提升度(lift):
用置信度/提升度;表示含有A的条件下同时含有B的概率,与只看发生B的概率之比
Lift(X→Y) = P(Y|X) / P(Y)
4.项:
对于数据表,表的每个字段都具有一个或多个不同的值,每个字段的每一种取值都是一个项
5.项集:
项的集合称为项集itemset。包含k个项的项集被称为k-项集,k表示项集中项的数目。由所有的项所构成的集合是最大的项集,一般用符号I表示。
6.事务:
一个事务本质上就是数据表的一个记录,事务的集合称为事务集,一般用D表示
7.关联规则:
给定一个事务集D,挖掘关联规则的问题就变成如何产生支持度和可信度分别大于用户给定的最小支持度和最小可信度的关联规则的问题
8.频繁项集:
项集的出现频率是包含项集的事务数,项集满足最小支持度阈值minsup,如果项集的出现频率大于或等于minsup与D中事务总数的乘积;满足最小支持阈值的项集就称为频繁项集(大项集)。频繁k项集的集合记为Lk
9.强关联规则:
大于或等于最小支持度阈值和最小置信度阈值的规则叫做强关联规则
基本思想:
对于Apriori算法,我们用支持度作为判断频繁项集的标准,该算法是要找到最大的K项频繁集,对于频繁项集来说:
1.所有的非空子集也都是频繁的,比如{1,2}是频繁的,那么{1},{2},也是频繁的;同样的反过来看,如果{1},{2}是频繁的,那么{1},{2}的超集也是频繁的。
2.任何非频繁的超集一定是非频繁的。
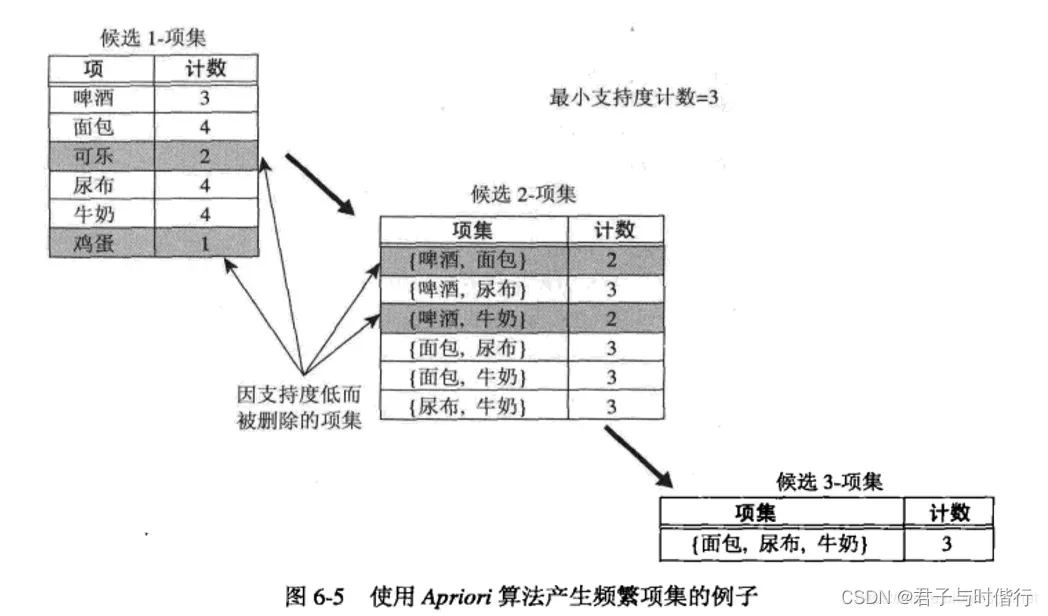
现在应该思考Apriori是怎么得到最多的K项频繁集?
Apriort算法采用迭代的思维,先找到候选1项集及对应得支持度,去掉低于支持度阈值的1项集后,就得到了频繁1项集。
继续用频繁1项集进行连接(排列组合),得到候选2项集,筛选掉低于支持度阈值的候选2项集,得到频繁2项集
以此类推,一直迭代下去,直到无法找到k+1项频繁集
例如:
优点和缺点:
优点:适合稀疏数据集
算法原理简单,易于实现
适合事务数据库的关联规则挖掘
缺点;
会产生庞大数据集
算法需要多次遍历数据集,算法效率低,耗时
代码实现(检索频繁集):
def loadDataSet():
"返回测试数据"
return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
# 创建候选1项集
def createC1(dataSet):
C=[ ]
for tid in dataSet:
for item in tid:
if not [item] in C:
C.append([item])
C.sort()
# frozenset:返回冻结集合,不能再添加或者删除元素
return list(map(frozenset,C))
# 三个参数分别为数据集D、候选项集列表Ck以及最小支持度minSupport
# 计算候选集集的支持度并选出k项频繁集
"""
输入:D:数据集(set格式)
Ck:候选集
minSupport:最小支持度
输出:retList:过滤集
supportData:支持集(挖掘关联规则使用)
"""
def scanD(D,Ck,minSupport):
# 统计元素出现次数
ssCnt = {}
for tid in D:
for can in Ck:
if can.issubset(tid):
if not ssCnt.has_key(can): ssCnt[can] = 1
else: ssCnt[can] += 1
# 构建过滤集和支持集
numItems = float(len(D))
retList = []
supportData = {}
for key in sscnt:
support = ssCnt[key] / numItems
if support >= minSupport:
retList.inset(0,key)
supportData[key] = support
return retList,supportData
"""
输入:
Lk:过滤集
k:当前项集元素个数
输出:
retList:候选集
"""
def aprioriGen(Lk,k):
# 由过滤集得到候选集
retList = []
lenLk = len(k)
for i in range(lenLk):
for j in range(i+1,lenLk)
L1 = list(Lk(i))[:k-2]
L2 = list(Lk[j])[:k-2]
L1.sort()
L2.sort()
if L1==L2:
retList.append(Lk[i] | Lk[j])
return retList
"""
输入:
dataSet: 数据集
minSupport:最小支持度
输出:
L:频繁集
supportData: 支持集(挖掘关联规则使用)
"""
def apriori(dataSet,minSupport = 0.5)
# 求频繁项集以及对应支持度
C1 = createC1(dataSet)
D = map(set,dataSet)
L1,supportData = scanD(D,C1,minSupport)
L = [L1]
k = 2
while(len(l[k-2])>0):
Ck = aprioriGen(l[K-2],k)
Lk,supK = scanD(D,Ck,minSupport)
supportData.update(supK)
L.append(Lk)
k += 1
return L,supportData
# Apriori频繁集检索
def main():
L,s = apriori(loadDataSet())
print(L)
print(s)关联规则代码实现:
"""
输入:
L:频繁集
supportData:支持集
minConf:最小可信度
输出:
bigRuleList:规则集
"""
def generateRules(L,supportData,minconf=0.7)
bigRuleList = []
for i in range(1,len(L)):
for freqSet in L[i]:
H1 = [frozenset(item) for item in freqSet]
if(i>1):
rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
else:
calcConf(freqSet,H1,supportData,bigRuleList,minConf)
return bigRuleList
"""
输入:
L:频繁集
supportData:支持集
minConf:最小可信度
输出:
bigRuleList:规则集
"""
def calcConf(freqSet,H,supportData,brl,minConf):
# 可信度过滤
prunedH = []
for conseq in H:
conf =supportData[freqSet] / supportData[freqSet-conseq]
if conf >= minConf:
brl.append((freqSet-conseq,conseq,conf))
prunedH.append(conseq)
return prunedH
def rulesFromConseq(freqSet,H,supportData,brl,minConf=0.7):
# 从频繁项集中学习关联规则
# 本次学习的规则右部中的元素个数
m = len(H(0))
if (len(freqSet) > (m+1)):
# 重组右部规则
Hmp1 = aprioriGen(H,m+1)
# 学习规则
Hmp1 = calcConf(reqSet,Hmp1,supportData,brl,minConf)
if(len(Hmp1)>1):
# 递归学习函数
rulesFromConseq(freqSet,Hmp1,supportData,brl,minConf)
def main():
L,s = apriori(loadDataSet())
rules = generateRules(L,s)
print(rules)案例:
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori
from mlxtend.frequent_patterns import association_rules
import pandas as pd
df_arr = [['苹果','香蕉','鸭梨'],
['橘子','葡萄','苹果','哈密瓜','火龙果'],
['香蕉','哈密瓜','火龙果','葡萄'],
['橘子','橡胶'],
['哈密瓜','鸭梨','葡萄']
]
#转换为算法可接受模型(布尔值)
te = TransactionEncoder()
df_tf = te.fit_transform(df_arr)
df = pd.DataFrame(df_tf,columns=te.columns_)
#设置支持度求频繁项集
frequent_itemsets = apriori(df,min_support=0.4,use_colnames= True)
#求关联规则,设置最小置信度为0.15
rules = association_rules(frequent_itemsets,metric = 'confidence',min_threshold = 0.15)
#设置最小提升度
rules = rules.drop(rules[rules.lift <1.0].index)
#设置标题索引并打印结果
rules.rename(columns = {'antecedents':'from','consequents':'to','support':'sup','confidence':'conf'},inplace = True)
rules = rules[['from','to','sup','conf','lift']]
print(rules)
#rules为Dataframe格式,可根据自身需求存入文件
# 结果如下:
'''
from to sup conf lift
0 (哈密瓜) (火龙果) 0.4 0.666667 1.666667
1 (火龙果) (哈密瓜) 0.4 1.000000 1.666667
2 (哈密瓜) (葡萄) 0.6 1.000000 1.666667
3 (葡萄) (哈密瓜) 0.6 1.000000 1.666667
4 (葡萄) (火龙果) 0.4 0.666667 1.666667
5 (火龙果) (葡萄) 0.4 1.000000 1.666667
6 (哈密瓜, 葡萄) (火龙果) 0.4 0.666667 1.666667
7 (哈密瓜, 火龙果) (葡萄) 0.4 1.000000 1.666667
8 (葡萄, 火龙果) (哈密瓜) 0.4 1.000000 1.666667
9 (哈密瓜) (葡萄, 火龙果) 0.4 0.666667 1.666667
10 (葡萄) (哈密瓜, 火龙果) 0.4 0.666667 1.666667
11 (火龙果) (哈密瓜, 葡萄) 0.4 1.000000 1.666667
Process finished with exit code 0
'''文章出处登录后可见!
