深度滤波器推导

测量不确定性

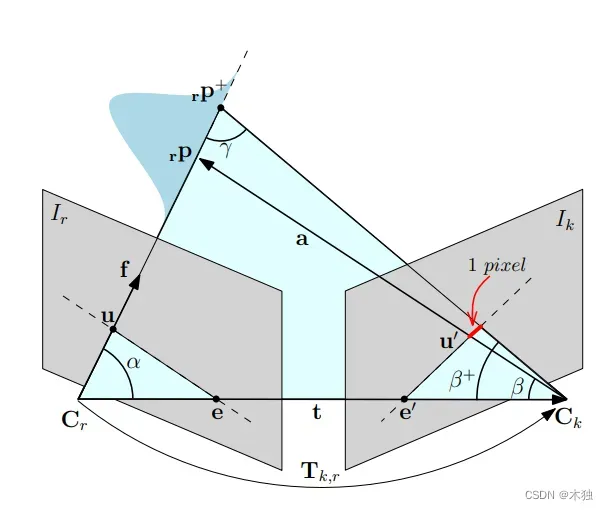
图像深度滤波器推导与对应的相机中心分别为。二者的转换关系为,并且平移距离为, 估计场景中的3d点为.假设匹配误差为一个像素，得到的误差距离为。

因此有：
深度滤波器推导

角度
深度滤波器推导

深度滤波器推导

因此得到，
深度滤波器推导

最终得到测量不确定度为

深度滤波器推导

代码分析

基本就是一条条公式对应过来

double DepthFilter::computeTau(
      const SE3& T_ref_cur,
      const Vector3d& f,
      const double z,
      const double px_error_angle)
{
  Vector3d t(T_ref_cur.translation());
  Vector3d a = f*z-t;
  double t_norm = t.norm();
  double a_norm = a.norm();
  double alpha = acos(f.dot(t)/t_norm); // dot product
  double beta = acos(a.dot(-t)/(t_norm*a_norm)); // dot product
  double beta_plus = beta + px_error_angle;
  double gamma_plus = PI-alpha-beta_plus; // triangle angles sum to PI
  double z_plus = t_norm*sin(beta_plus)/sin(gamma_plus); // law of sines
  return (z_plus - z); // tau
}

深度滤波器

采用高斯分布与均匀分布叠加的概率密度函数表达深度信息的分布。

好处：提高算法对于错误匹配的鲁棒性
坏处：公式推导过程复杂，实现计算量稍大

包含四个参数分别为高斯分布的深度滤波器推导与均匀分布的。

深度滤波器推导

迭代更新过程

已知：
上一次的概率分布深度滤波器推导
当前的测量值

求解更新后的概率分布深度滤波器推导

计算过程

深度滤波器推导

深度滤波器推导
这里的代表高斯分布在位置的概率分布，同理为均匀分布在x位置处的概率。

深度滤波器推导

更新概率分布
深度滤波器推导

深度滤波器推导

更新均匀分布
深度滤波器推导

深度滤波器推导

代码分析

基本能和上面的公式对应起来

void DepthFilter::updateSeed(const float x, const float tau2, Seed* seed)
{
  float norm_scale = sqrt(seed->sigma2 + tau2);
  if(std::isnan(norm_scale))
    return;
  boost::math::normal_distribution<float> nd(seed->mu, norm_scale);
  float s2 = 1./(1./seed->sigma2 + 1./tau2);
  float m = s2*(seed->mu/seed->sigma2 + x/tau2);
  float C1 = seed->a/(seed->a+seed->b) * boost::math::pdf(nd, x);
  float C2 = seed->b/(seed->a+seed->b) * 1./seed->z_range;
  float normalization_constant = C1 + C2;
  C1 /= normalization_constant;
  C2 /= normalization_constant;
  float f = C1*(seed->a+1.)/(seed->a+seed->b+1.) + C2*seed->a/(seed->a+seed->b+1.);
  float e = C1*(seed->a+1.)*(seed->a+2.)/((seed->a+seed->b+1.)*(seed->a+seed->b+2.))
          + C2*seed->a*(seed->a+1.0f)/((seed->a+seed->b+1.0f)*(seed->a+seed->b+2.0f));

  // update parameters
  float mu_new = C1*m+C2*seed->mu;
  seed->sigma2 = C1*(s2 + m*m) + C2*(seed->sigma2 + seed->mu*seed->mu) - mu_new*mu_new;
  seed->mu = mu_new;
  seed->a = (e-f)/(f-e/f);
  seed->b = seed->a*(1.0f-f)/f;
}