论文:Gradient Harmonized Single-stage Detector
论文地址:Gradient Harmonized Single-stage Detector![]() https://arxiv.org/pdf/1811.05181.pdf
https://arxiv.org/pdf/1811.05181.pdf
注意 PPT图片为实验室论文研讨组会讲解所需,为笔者自己所做,慎用!
Research Problems(问题)
对于一阶段目标检测器的训练来说,最具挑战性的问题是: 简单和困难样本的急剧不平衡 与 正负样本的急剧不平衡 -> 并且这两种可以大致概括为 属性不均衡问题
类别不平衡能被概括为样本难易程度不一致的问题,而后样本难易程度不一致的问题能被概括为梯度范数分布不均的问题[这是GHM论文中的原话,但是笔者不这么认为类别不平衡问题可概括为样本难易程度不一致问题]
如果一个正样本是易分类的样本,那它是一个简单样本,并且(再次训练时)模型从这个样本上收益很少,换言之,这种样本将产生极少的梯度。
一个误分类样本,不管属于什么类别,都应该引起模型的注意
(i.e.)换言之

尽管,单个简单样本比单个困难样本在全局梯度上有更少的贡献,但是大量简单样本总的贡献能压倒少量的困难样本从而导致这种训练效率低下
GHM(Gradient Harmonized Mechanism) 梯度均衡机制 首先对相同属性的样本 数量 及 其梯度密度进行统计,然后根据 样本的梯度密度 附上一个协调参数
(w.r.t.)关于

主要贡献
依据梯度范数分布,揭示了一阶段目标检测器严重样本不平衡的基本原理,并提出了一种新的 梯度均衡机制 来处理此不均衡
将 GHM-C(分类的梯度均衡机制) 与 GHM-R(回归的梯度均衡机制) 分别嵌入到分类与回归损失函数中,纠正了不同属性的样本梯度贡献,并对超参数具有鲁棒性
通过GHM的协作,在没有任何数据采样策略下,能容易训练一阶段检测器,并且在COCO基准达到最先进的结果

流程图
本文主要是以RetinaNet为基准对其损失函数进行修改,所以其流程图主要参照RetinaNet:
算法
梯度均衡机制
1.对于分类的梯度均衡机制来说
首先从二分类交叉熵损失函数开始,
其中,为模型的预测值,
为样本标签
当时(正样本),
当时(负样本),
关于x的梯度,sigmoid,其中p为头网络的输出结果,x为特征图
现在求关于x的一阶导数即是
当时(正样本),
当时(负样本),
即,对
的一阶导数
(当
,
;当
,
),并且
可表示样本的真实值与预测值之间的距离

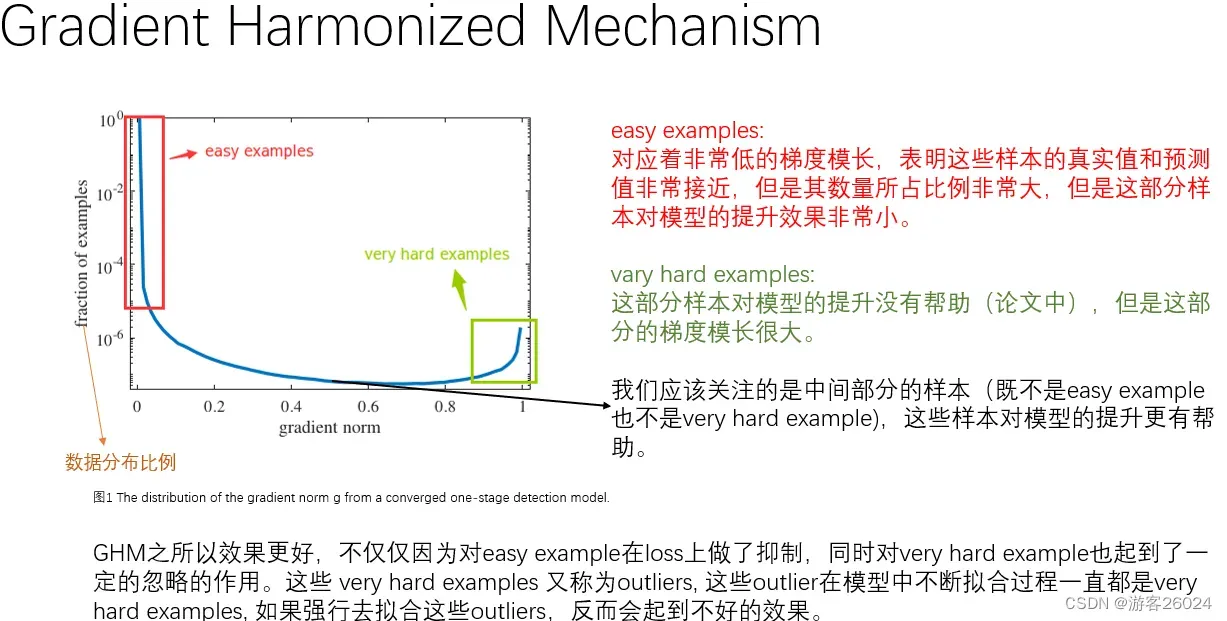
在图1中,横坐标表示梯度范数(梯度模长),纵坐标表示样本数据分布比例;
在此的梯度范数(梯度模长),是我们刚才算出的(
对于
的一阶导数
)
分析图1,简单样本已由红框框出,其梯度范数(梯度模长)非常低,表明这些样本的真实值和预测值非常接近,并且其数量所占比例非常大,但是这部分样本(再次训练)对模型的提升效果非常有限。
非常困难样本以由绿框框出,这部分样本对模型的提升是没有什么帮助的,但是这部分的样本的梯度范数(梯度模长)很大
介于既 不是简单样本 也不是特别困难样本 中间部分的样本(黑色箭头标出),这些样本对模型的提升更有帮助
从之后的结果来看,GHM之所以效果比焦点损失更好,不仅仅因为其对简单样本在损失上做了抑制,同时对非常困难的样本也起到了一定的忽略作用。这些非常困难样本又被称之为离群点,这些离群点在模型中不断拟合过程一直起到了重要作用,如果强行拟合这些离群点,反而会起到不好的效果
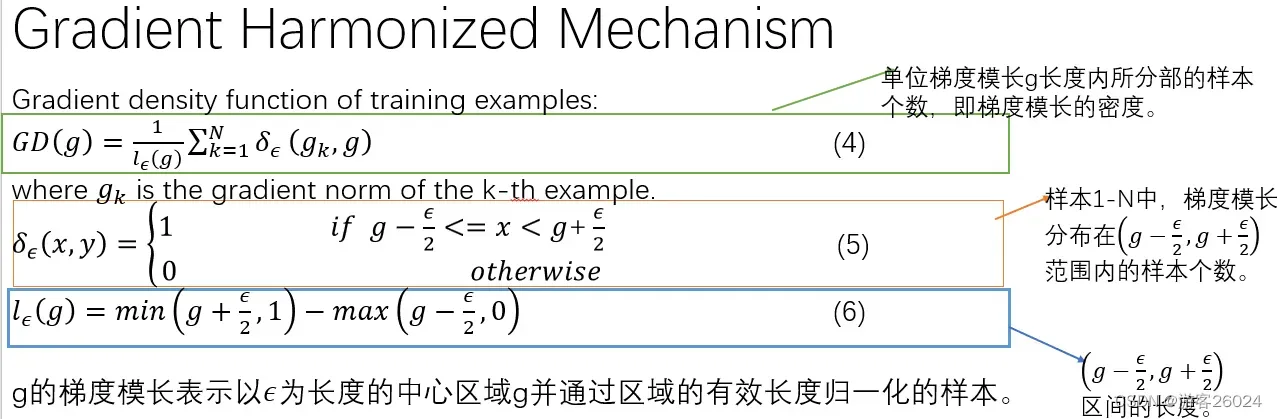
接下来,定义梯度范数(梯度模长)的密度;在此之前我们必须要先定义梯度范数(梯度模长)范围内的样本个数
在梯度范数(梯度模长)范围内,样本的个数
;如果是范围内则
,反之范围外则
之后,定义范数(模长)区间
所以,单位梯度模长内样本的个数->梯度模长的密度
g的梯度模长表示以为长度的中心区域
,并且通过该区域将样本的长度归一化
然后,定义梯度密度均衡参数,其中N为样本的总数
当很大时,可通过
抑制;对于梯度密度大的样本,即
的值很大,则
相应变小,而
对应变大;反之,当
很小时,则
相应变大,而
对应变小;
从之前的图1可以看出,简单样本和非常困难样本的分布非常密集;
如果样本梯度是均衡分布的,那么对于任何和每一个样本,
且
,相比与之前没做此操作时,是没有任何变化的

好了,将我们刚才所定义的梯度密度均衡参数引入我们之前的分类损失函数中,则可得
,其中
可以视为第i个样本的损失权重(
第i个样本的梯度密度均衡参数)

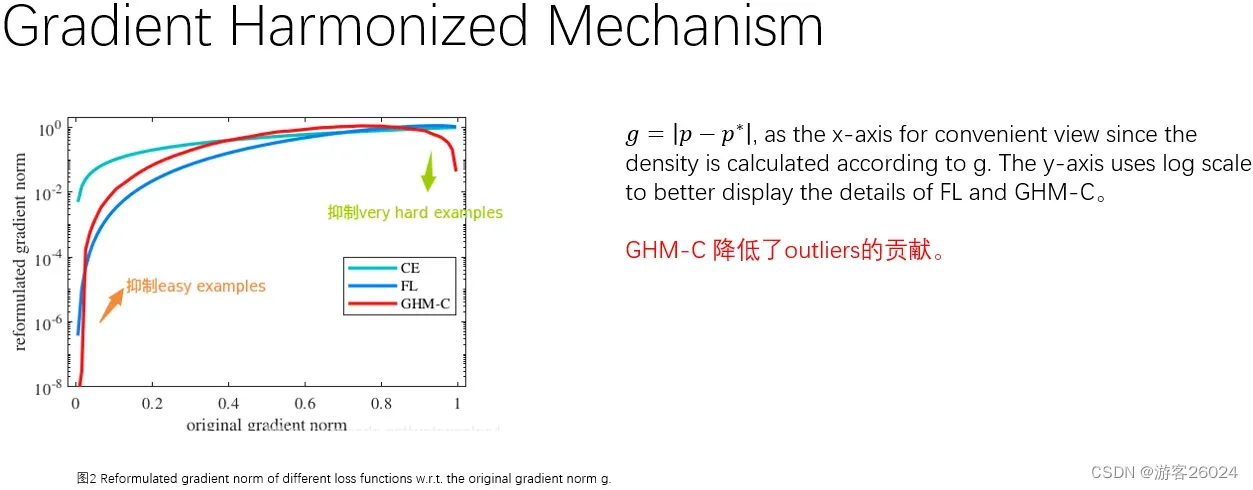
在图2中,横坐标为原始梯度范数(梯度模长),纵坐标为重新修正的梯度范数,使用log 缩放能更好的展示 焦点损失函数 与 关于分类的梯度均衡机制
分析图2,我们 关于分类的梯度均衡机制 能同时更好的抑制简单样本,与特别困难样本,降低了离群点的贡献
我们可以使用EMA,简化该过程





2.对于回归的梯度均衡机制来说
简言之,因为二阶导数,在
不可导,所以我们将其修改为
,并且找出与一个相对于回归的损失权重
,引入回归损失函数中


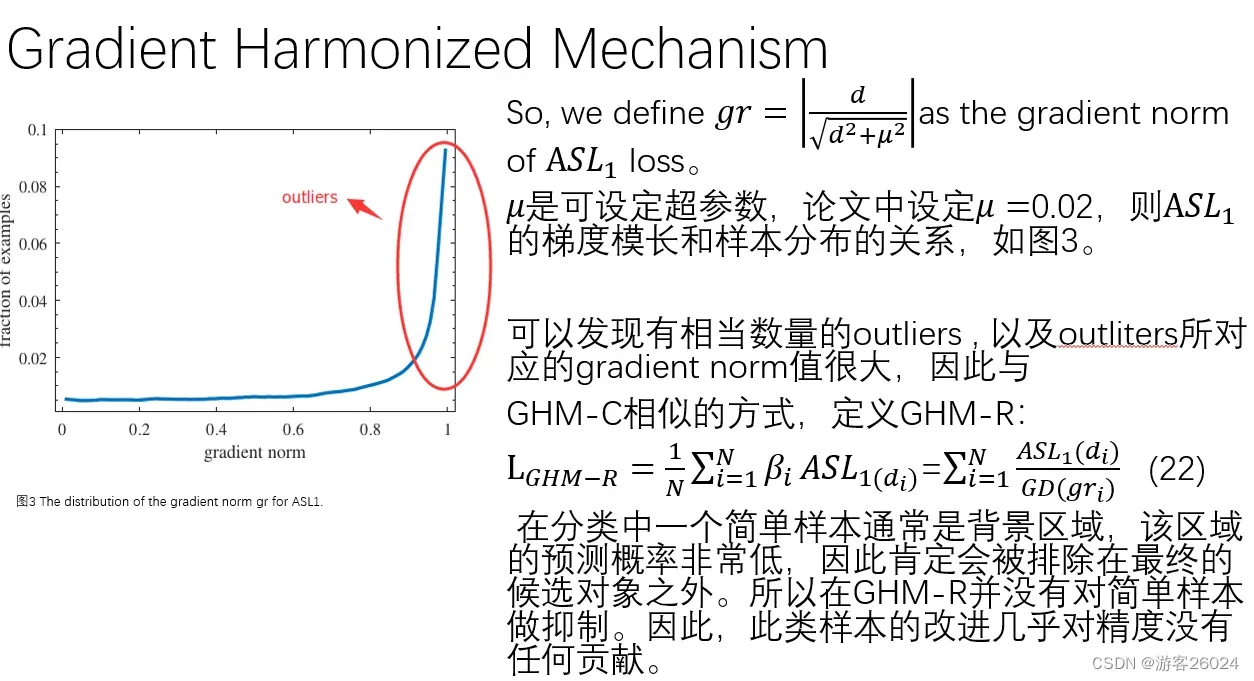
在图3中,横坐标为梯度范数(梯度模长),纵坐标为样本分布
分析图3可知,我们的离群点最为突出,我们使用GHM-R对其抑制
此外,在分类中一个简单样本通常是背景区域,该区域的预测概率非常低,因此肯定会排除在最终的候选对象之外,所以 关于回归的梯度均衡机制 对此类简单样本抑制。因此,此类样本的改进几乎对精度没有任何贡献
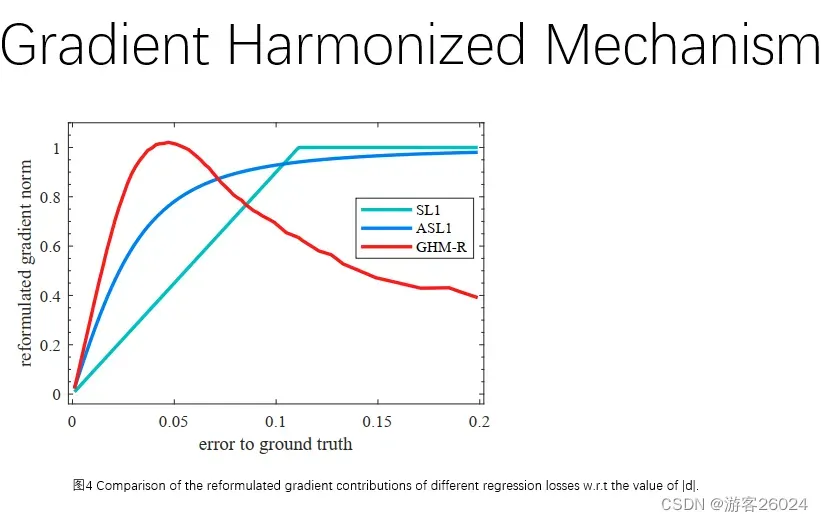
在图4中,横坐标为关于标签的错误率,纵坐标为重新修正的梯度范数(梯度模长)
分析图4可知,我们的GHM-R对于与
效果更好!
The End
文章出处登录后可见!
