(三)朴素贝叶斯分类器
朴素贝叶斯分类器是一种与线性模型非常相类似的一种分类器。
原理:通过独立查看每个特征来学习参数,并从每个特征中收集简单的类别统计数据
性能:训练速度比线性模型更快,但是泛化能力要强。
类别:1.GaussianNB(任意连续数据) 2.BernoulliNB(二分类数据) 3.MultinomNB(计数数据)
BernoulliNB计算每个类别中特征不为0的元素个数:
(1)数据点(4个,每个二分类特征)
X = np.array([[0, 1, 0, 1],
[1, 0, 1, 1],
[0, 0, 0, 1],
[1, 0, 1, 0]])
y = np.array([0, 1, 0, 1])
(2)计算每个类别中的非零元素个数
counts = {}
for label in np.unique(y):
counts[label] = X[y == label].sum(axis=0)
print("Feature counts:\n", counts)
Feature counts:
{0: array([0, 1, 0, 2]), 1: array([2, 0, 2, 1])}
想要做出预测,需要将数据点与每个类别的统计数据进行比较,将最匹配的类别作为预测结果。
优缺点、参数:
参数:alpha(BernoulliNB、MultinomNB)
alpha越大,平滑化越强,模型复杂度越低。对于模型性能不重要,但能使精度略有提高
优缺点:类似线性模型
(四)决策树
决策树是广泛用于分类和回归任务的模型。
区分几种动物的决策树:
mglearn.plots.plot_animal_tree()
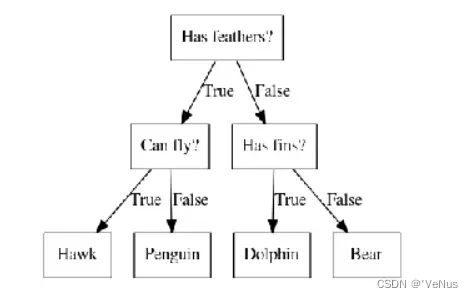
图中树的每个结点表示一个问题或者一个包含答案的结点,将答案和下个问题连接起来
1、构造决策树
二维分类数据集(two_moons数据集)上构造决策树:
mglearn.plots.plot_tree_progressive()
学习决策树,就是学习一系列的if/else问题(这些问题被叫做测试),使得能够以最快速度得到正确答案
构造决策树,算法搜遍所有可能的测试,找出对目标变量来说信息量最大的那一个。
对数据进行反复递归划分,指导划分后的每一个区域只包含单一目标值(叶结点就是纯的)。
进行预测,查看这个点位于特征空间划分的哪个区域,然后将该区域的多数目标值作为预测结果
完成回归任务,方法相同,找到叶结点后,输出叶结点中平均目标值。
2、控制决策树的复杂度
控制决策树的复杂度,防止过拟合。
两种常见的策略:
1、预剪枝(pre-pruning):及早停止树的生长
2、后剪枝(post-pruning)\ 剪枝(pruning):先构造树,但随后删除或折叠信息量很少的结点
预剪枝条件:限制树的最大深度、叶节点的最大数目、规定一个节点中数据点的最小数目
scikit-learn 的决策树在 DecisionTreeRegressor 类和 DecisionTreeClassifier 类中实现。
(1)在乳腺癌数据集上应用预剪枝
from sklearn.tree import DecisionTreeClassifier
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))
Accuracy on training set: 1.000
Accuracy on test set: 0.937
训练集上的精度是 100%,叶结点都是纯的,树的深度很大,完美地记住训练数据的所有标签。
(2)决策树上应用预剪枝(限制树的深度)
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))
Accuracy on training set: 0.988
Accuracy on test set: 0.951
降低了训练集精度,但是可以提高测试集的精度
3、分析决策树
使用tree.export_graphviz将树可视化,生成一种文件可以保存图形的文本文件格式
利用grahviz模块读取文件并可视化
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["malignant", "benign"],
feature_names=cancer.feature_names, impurity=False, filled=True)
import graphviz
with open("tree.dot") as f:
dot_graph = f.read()
display(graphviz.Source(dot_graph))
4、树的特征重要性
利用有用的属性总结树的原理,最常用:特征重要性(feature importance)
(1)输出
print("Feature importances:")
print(tree.feature_importances_)
Feature importances:
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.01 0.048
0. 0. 0.002 0. 0. 0. 0. 0. 0.727 0.046 0. 0.
0.014 0. 0.018 0.122 0.012 0. ]
(2)可视化
def plot_feature_importances_cancer(model):
n_features = cancer.data.shape[1]
plt.barh(np.arange(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), cancer.feature_names)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
plot_feature_importances_cancer(tree)
)
(3)二维数据集与决策树给出的决策边界
tree = mglearn.plots.plot_tree_not_monotone()
display(tree)
难以说明哪个特征对应哪个类别
(4)数据集
import os
ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH, "ram_price.csv"))
plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("Year")
plt.ylabel("Price in $/Mbyte")
(5)利用2000年前数据预测2000年后价格,日期为特征,对比模型
from sklearn.tree import DecisionTreeRegressor
data_train = ram_prices[ram_prices.date < 2000]
data_test = ram_prices[ram_prices.date >= 2000]
#预测价格
X_train = data_train.date[:, np.newaxis]
y_train = np.log(data_train.price)
tree = DecisionTreeRegressor(max_depth=3).fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)
#对所有数据预测
X_all = ram_prices.date[:, np.newaxis]
pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)
# 对数变换逆运算
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)
(6)线性模型和回归树对RMB价格数据的预测数据对比
plt.semilogy(data_train.date, data_train.price, label="Training data")
plt.semilogy(data_test.date, data_test.price, label="Test data")
plt.semilogy(ram_prices.date, price_tree, label="Tree prediction")
plt.semilogy(ram_prices.date, price_lr, label="Linear prediction")
plt.legend()
5、优缺点、参数
优点:
1、得到的模型很容易可视化,非专家也很容易理解
2、算法完全不受数据缩放的影响,不需要特征预处理。
缺点:即使做了预剪枝,它也经常会过拟合,泛化性能很差。
参数:控制决策树模型复杂度的参数是预剪枝参数,它在树完全展开之前停止树的构造。通常来说,选择一种预剪枝策略(设置 max_depth 、 max_leaf_nodes 或 min_samples_leaf )足以防止过拟合。
(五)决策树集成
集成(ensemble)是合并多个机器学习模型来构建更强大模型的方法。已证明有两种集成模型对大量分类和回归的数据集都是有效的,都以决策树为基础
模型:随机森林(random forest)、梯度提升决策树(gradient boosted decision tree)。
1、随机森林
决策树的一个主要缺点在于经常对训练数据过拟合。随机森林是解决这个问题的一种方法。
随机森林本质上是许多决策树的集合,其中每棵树都和其他树略有不同。
原理:每棵树的预测可能都相对较好,但可能对部分数据过拟合。
分析随机森林
【例1】
数据集:make_moons
模型:随机森林(5棵树)
(1)
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
random_state=42)
forest = RandomForestClassifier(n_estimators=5, random_state=2)
forest.fit(X_train, y_train)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion=‘gini’,
max_depth=None, max_features=‘auto’, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=5, n_jobs=None,
oob_score=False, random_state=2, verbose=0, warm_start=False)
(2)决策边界、总预测可视化
fig, axes = plt.subplots(2, 3, figsize=(20, 10))
for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
ax.set_title("Tree {}".format(i))
mglearn.plots.plot_tree_partition(X_train, y_train, tree, ax=ax)
mglearn.plots.plot_2d_separator(forest, X_train, fill=True, ax=axes[-1, -1],
alpha=.4)
axes[-1, -1].set_title("Random Forest")
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
每棵树决策边界不同,都犯了错误,原因在于自主采样。
【例2】
数据集:乳腺癌
模型:100棵树
(1)
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
forest = RandomForestClassifier(n_estimators=100, random_state=0)
forest.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(forest.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(forest.score(X_test, y_test)))
Accuracy on training set: 0.988
Accuracy on test set: 0.965
默认情况下比线性模型和单棵决策树精度都好。
一般来说随机森林的特征重要性比单棵决策树的更可靠
2、梯度提升回升树(梯度提升机)
梯度提升回归树是另一种集成方法,通过合并多个决策树来构建一个更为强大的模型。
梯度提升的一个重要参数是 learning_rate (学习率),用于控制每棵树纠正前一棵树的错误的强度。
(1)
from sklearn.ensemble import GradientBoostingClassifier
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))
Accuracy on training set: 1.000
Accuracy on test set: 0.958
(2)
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))
Accuracy on training set: 0.991
Accuracy on test set: 0.972
(3)
gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.01)
gbrt.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))
Accuracy on training set: 0.988
Accuracy on test set: 0.965
(4)
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
plot_feature_importances_cancer(gbrt)
3、优缺点、参数
参数:n_estimators(树的数量) 、 learning_rate(学习率)、max_depth \ max_leaf_nodes
n_estimators:树的数量
learning_rate:控制每棵树对前一棵树的错误的纠正强度
max_depth :降低每棵树的复杂度
优点:与其他基于树的模型类似,这一算法不需要对数据进行缩放就可以表现得很好,而且也适用于二元特征与连续特征同时存在的数据集。
缺点:需要仔细调参,而且训练时间可能会比较长,不适用于高维稀疏数据。
(六)核支持向量机
核支持向量机(SVM)是可以推广到更复杂模型的扩展,这些模型无法被输入空间的超平面定义。
1、线性模型与非线性特征
(1)
X, y = make_blobs(centers=4, random_state=8)
y = y % 2
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
(2)
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)
mglearn.plots.plot_2d_separator(linear_svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
(3)
# add the squared first feature
X_new = np.hstack([X, X[:, 1:] ** 2])
from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()
# visualize in 3D
ax = Axes3D(figure, elev=-152, azim=-26)
# plot first all the points with y==0, then all with y == 1
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
cmap=mglearn.cm2, s=60, edgecolor='k')
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")
(4)
linear_svm_3d = LinearSVC().fit(X_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_
# show linear decision boundary
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
XX, YY = np.meshgrid(xx, yy)
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
cmap=mglearn.cm2, s=60, edgecolor='k')
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")
(5)
ZZ = YY ** 2
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])
plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()],
cmap=mglearn.cm2, alpha=0.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
2、核技巧
原理:直接计算扩展特征表示中数据点之间的距离(内积),而不用实际对扩展进行计算。
方法:
1、多项式核:计算原始特征所有可能的多项式
2、径向基函数核(RBF核)\ 高斯核:考虑所有阶数的所有可能的多项式,但阶数越高,特征的重要性越小
3、理解SVM
在训练过程中,SVM学习每个训练数据点对于两个类别之间的决策边界的重要性,而通常只有一部分训练数据点对于定义决策边界很重要:位于决策边界上的那些点(支持向量)。
想要对新的样本点进行预测,需要测量它与每个支持向量的距离。
分类决策是基于它与支持向量之间的距离以及训练过程中学到的支持向量重要性来做出的。
from sklearn.svm import SVC
X, y = mglearn.tools.make_handcrafted_dataset()
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
sv = svm.support_vectors_
sv_labels = svm.dual_coef_.ravel() > 0
mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15, markeredgewidth=3)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
4、SVM调参
参数:kernel、gamma、c
(1)
fig, axes = plt.subplots(3, 3, figsize=(15, 10))
for ax, C in zip(axes, [-1, 0, 3]):
for a, gamma in zip(ax, range(-1, 2)):
mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)
axes[0, 0].legend(["class 0", "class 1", "sv class 0", "sv class 1"],
ncol=4, loc=(.9, 1.2))
(2)
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
svc = SVC()
svc.fit(X_train, y_train)
print("Accuracy on training set: {:.2f}".format(svc.score(X_train, y_train)))
print("Accuracy on test set: {:.2f}".format(svc.score(X_test, y_test)))
Accuracy on training set: 1.00
Accuracy on test set: 0.63
(3)
plt.boxplot(X_train, manage_xticks=False)
plt.yscale("symlog")
plt.xlabel("Feature index")
plt.ylabel("Feature magnitude")
5、为SVM预处理数据
数据集的特征具有完全不同的数量级,对核SVM有极大影响,需要对每个特征进行缩放,使其大致都处于同一范围
(1)
min_on_training = X_train.min(axis=0)
range_on_training = (X_train - min_on_training).max(axis=0)
X_train_scaled = (X_train - min_on_training) / range_on_training
print("Minimum for each feature\n", X_train_scaled.min(axis=0))
print("Maximum for each feature\n", X_train_scaled.max(axis=0))
Minimum for each feature
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.]
Maximum for each feature
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
- 1.]
(2)
X_test_scaled = (X_test - min_on_training) / range_on_training
(3)
svc = SVC()
svc.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(
svc.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(svc.score(X_test_scaled, y_test)))
Accuracy on training set: 0.988
Accuracy on test set: 0.972
6、优缺点、参数
参数:
核SVM:正则化参数C、核的选择、核相关的参数
RBF核:gamma
优点:在各种数据集上表现都很好
缺点:对样本个数的缩放表现不好,预处理数据和调参需要非常小心
文章出处登录后可见!