目录

一、PyTorch简介

PyTorch是一个能在CPU和GPU上运行并解决各类深度学习问题的深度学习框架。可以将其看做是支持GPU计算和自动微分计算的Numpy库。

1.1 特点

• 易于使用的API
• Python的支持
• 动态计算图 
• 部署简单
• 支持分布式训练
• 支持移动端
• 强大的生态系统
• 内置开放的神经网络交换协议(ONNX)

1.2 GPU使用测试

import torch
# 以下代码只有在PyTorch GPU版本上才会执行
import time

print(torch.__version__)
print(torch.cuda.is_available())
a = torch.randn(10000, 1000)
b = torch.randn(1000, 2000)
t0 = time.time()
c = torch.matmul(a, b)
t1 = time.time()
print(a.device, t1 - t0, c.norm(2))

device = torch.device('cuda')
a = a.to(device)
b = b.to(device)
t0 = time.time()
c = torch.matmul(a, b)
t1 = time.time()
print(a.device, t1 - t0, c.norm(2))

t0 = time.time()
c = torch.matmul(a, b)
t1 = time.time()
print(a.device, t1 - t0, c.norm(2))

1.11.0
False
cpu 1.0578720569610596 tensor(140311.2656)

二、线性回归实例

2.1 线性回归模型原理

通用表达式

 数据导入(导入线性回归包)

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas import DataFrame,Series
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression

利用pandas和numpy对数据进行操作，使用matplotlib进行图像化 ，使用sklearn进行数据集训练与模型导入

# 创建数据集
examDict = {'学习时间': [0.50, 0.75, 1.00, 1.25, 1.50, 1.75, 1.75,
                     2.00, 2.25, 2.50, 2.75, 3.00, 3.25, 3.50, 4.00, 4.25, 4.50, 4.75, 5.00, 5.50],
            '分数': [10, 22, 13, 43, 20, 22, 33, 50, 62,
                   48, 55, 75, 62, 73, 81, 76, 64, 82, 90, 93]}

# 转换为DataFrame的数据格式
examDf = DataFrame(examDict)

plt.scatter(examDf.分数, examDf.学习时间, color='b', label="Exam Data")

# 添加图的标签（x轴，y轴）
plt.xlabel("Hours")
plt.ylabel("Score")
# 显示图像
plt.show()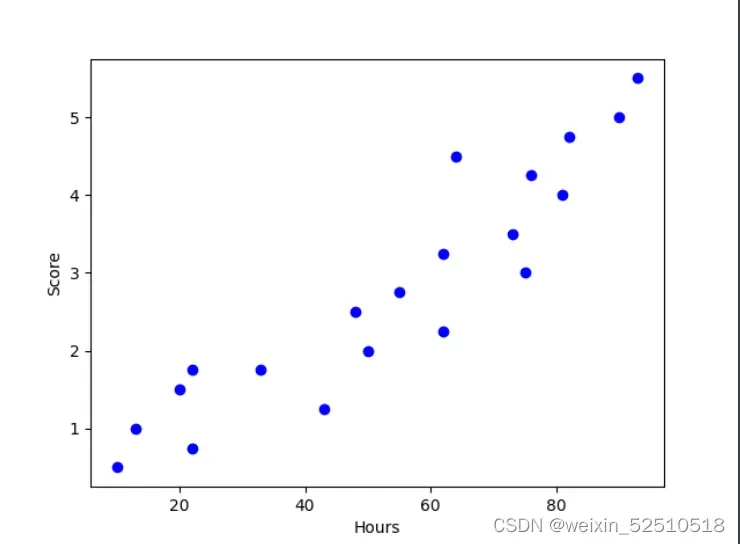

 从图我们可以看到对于分数和时间来说存在相应的线性关系，且俩数据间相关性较强。

对于相关性强度来说的化有以下的关系：

• 0-0.3    弱相关
• 0.3-0.6 中等强度相关
• 0.6-0.1  强相关

三、张量基础

3.1 概念

Tensors张量，与numpy中的ndarray类似，但是在pytorch中，Tensors可以使用GPU进行计算，张量的话可以默认记录计算轨迹，从而方便求导。

3.2 创建torch数据 

import torch
torch_1 = torch.eye(4,4)#创建一个4乘4维的张量
torch_2 = torch.zeros(4,4)#创建一个4乘4的全零张量
torch_3 = torch.arange(16).reshape(2,2,-1)#定义一个范围0~15，然后修改维度第一维度有两个，第二维度为2，第三维度-1：自动填充

print(torch_1)
print(torch_2)
print(torch_3)

tensor([[1., 0., 0., 0.],
        [0., 1., 0., 0.],
        [0., 0., 1., 0.],
        [0., 0., 0., 1.]])
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])
tensor([[[ 0,  1,  2,  3],
         [ 4,  5,  6,  7]],

        [[ 8,  9, 10, 11],
         [12, 13, 14, 15]]])

3.3 张量的类型

print(torch_1.shape)
print(torch_2.size())

torch.Size([4, 4])
torch.Size([4, 4]) 

3.4 张量的索引与切片

print(torch_1[2])
print(torch_1[:,1])
print(torch_3[:,1,:-1])

 tensor([0., 0., 1., 0.])
tensor([0., 1., 0., 0.])
tensor([[ 4,  5,  6],
        [12, 13, 14]])

3.5 将numpy转换成Tensors

arr = np.array([[1,2,3],[4,5,6]])
torch_4 = torch.from_numpy(arr)
print(arr,'\n',torch_4)

[[1 2 3]
 [4 5 6]] 
 tensor([[1, 2, 3],
        [4, 5, 6]]) 

 3.6 常用操作

3.6.1 torch.cat()

张量拼接

• 第一个参数: 元组。拼接的张量放进元组
• 第二个参数:拼接的轴

torch_5 = torch.arange(8).reshape(2,2,2)
torch_6 = torch.arange(12).reshape(3,2,2)
torch_cat = torch.cat((torch_5,torch_6),0)#拼接第0轴
print(torch_5,'\n',torch_6,'\n',torch_cat)

tensor([[[0, 1],
         [2, 3]],

        [[4, 5],
         [6, 7]]]) 
 tensor([[[ 0,  1],
         [ 2,  3]],

        [[ 4,  5],
         [ 6,  7]],

        [[ 8,  9],
         [10, 11]]]) 
 tensor([[[ 0,  1],
         [ 2,  3]],

        [[ 4,  5],
         [ 6,  7]],

        [[ 0,  1],
         [ 2,  3]],

        [[ 4,  5],
         [ 6,  7]],

        [[ 8,  9],
         [10, 11]]])

3.6.2  torch.squeeze、torch.unsqueeze

torch.squeeze 压缩维度，把维度为1的去掉

torch_squeeze = torch.squeeze(torch_6)#shape(1,1,4)去掉为1的维度
print('torch_squeeze.shape',torch_squeeze.shape)

torch_squeeze.shape torch.Size([3, 2, 2]) 

torch.unsqueeze 增加维度

• 第一个参数:操作的对象
• 第二个参数:增加维度的位置

torch_unsqueeze = torch.unsqueeze(torch_squeeze,1)
print('torch_unsqueeze.shape',torch_unsqueeze.shape)

torch_unsqueeze.shape torch.Size([3, 1, 2, 2]) 

3.6.3 torch.view

 重构张量 

print(torch_6.shape)
torch_view = torch_6.view(-1)

torch.Size([3, 2, 2]) 

 重构成一维

torch_reshape = torch_6.reshape(-1)
print('torch_view',torch_view)
print('torch_reshape',torch_reshape)

torch_view tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])
torch_reshape tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11]) 

 四、逻辑回归

机器学习中比较主流的一种分类算法，通常我们指的分类问题都是一个二分类问题，逻辑回归方法主要是针对二分类问题的。

4.1 算法步骤

• 通过自变量利用回归分析的思想得到因变量的预测值y
• 通过Sigmoid函数将因变量的预测值y–映射到(0,1)区间，设为w，w是分类为正类的概率
• 设立一个阈值，当w大于阈值时，将其分为正类，否则将其分为负类

4.2 步骤解释

第一步 把因变量和自变量找出，对其进行回归分析，得出因变量的预测值y

此时，y的取值是一个在负无穷到正无穷之间的数。

第二步 logistic函数为:

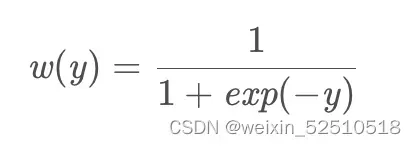
图像如图所示

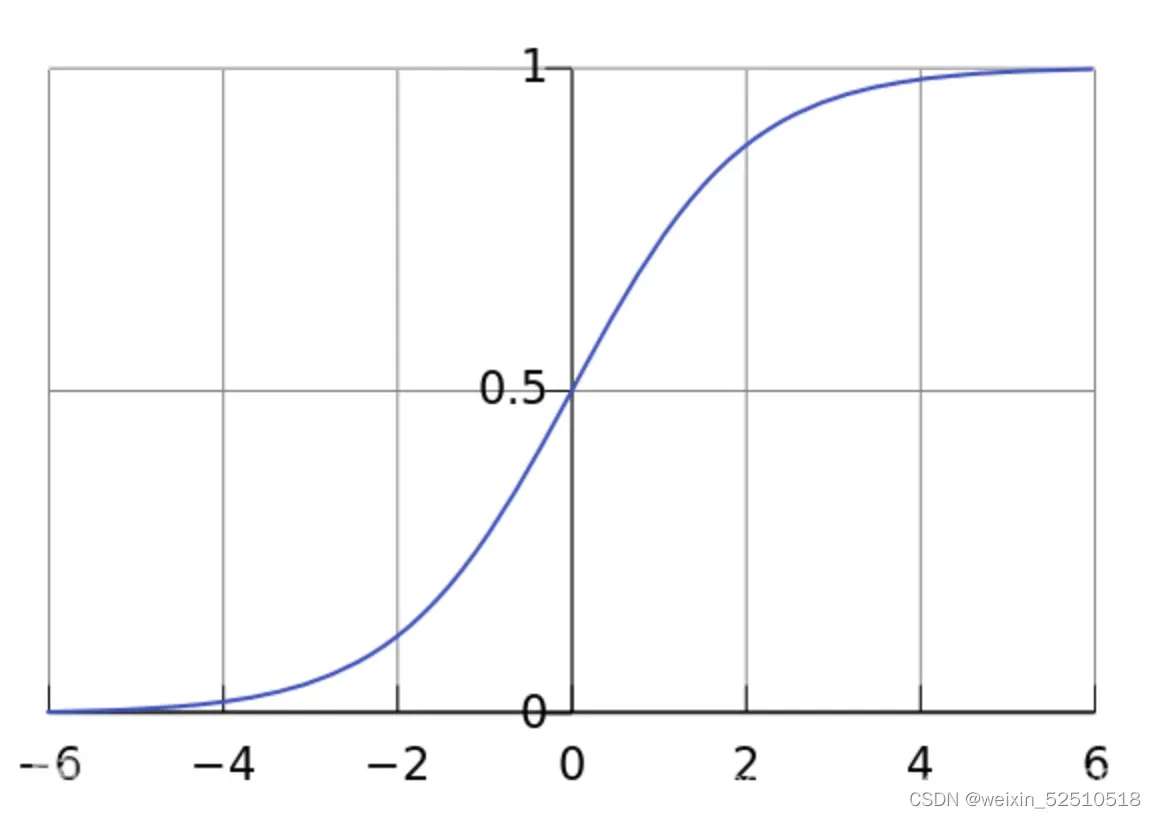
 从图像中，我们可以发现这是一个单调递增的函数，其定义域是 ( − ∞ , ∞ )，其值域为 ( 0 , 1 ) ，通过logistic函数，我们可以将预测值 y从 ( − ∞ , ∞ ) 一一映射到 ( 0 , 1 ) 内。

其中，w表示的分类为正类的概率

第三步  我们设立一个阈值（一般都是0.5），当分类为正类的概率大于这个阈值是，我们将其分为正类，当分类这个概率小于0.5时，我们将其分为负类。 

五、PyTorch的自动微分

在torch中的torch.autograd模块，提供了实现任意标量值函数自动求导的类和函数
例如:在pyTorch生成一个矩阵张量x，并且y=sum(x^2+2*x+1),计算y在x上的导数

import torch
x = torch.tensor([[1.0],[2.0],[3.0],[4.0]], requires_grad = True)
y = torch.sum(x**2 + 2*x + 1)
print("x.requires_grad:",x.requires_grad)
print("y.requires_grad:",y.requires_grad)
print("x:",x)
print("y:",y)

x.requires_grad: True
y.requires_grad: True
x: tensor([[1.],
        [2.],
        [3.],
        [4.]], requires_grad=True)
y: tensor(54., grad_fn=<SumBackward0>)

#计算y在x上的梯度
y.backward()
x.grad

tensor([[ 4., 6.],

             [ 8., 10.]] )

六、torch.nn模块

6.1 卷积层

卷积可以看作是输入和卷积核之间的内核运算，是两个实值函数之间的一种数学运算。在卷积函数中，通常使用卷积核将输入数据进行卷积运算得到输出作为特征映射每个卷积核可获得一个特征映射。

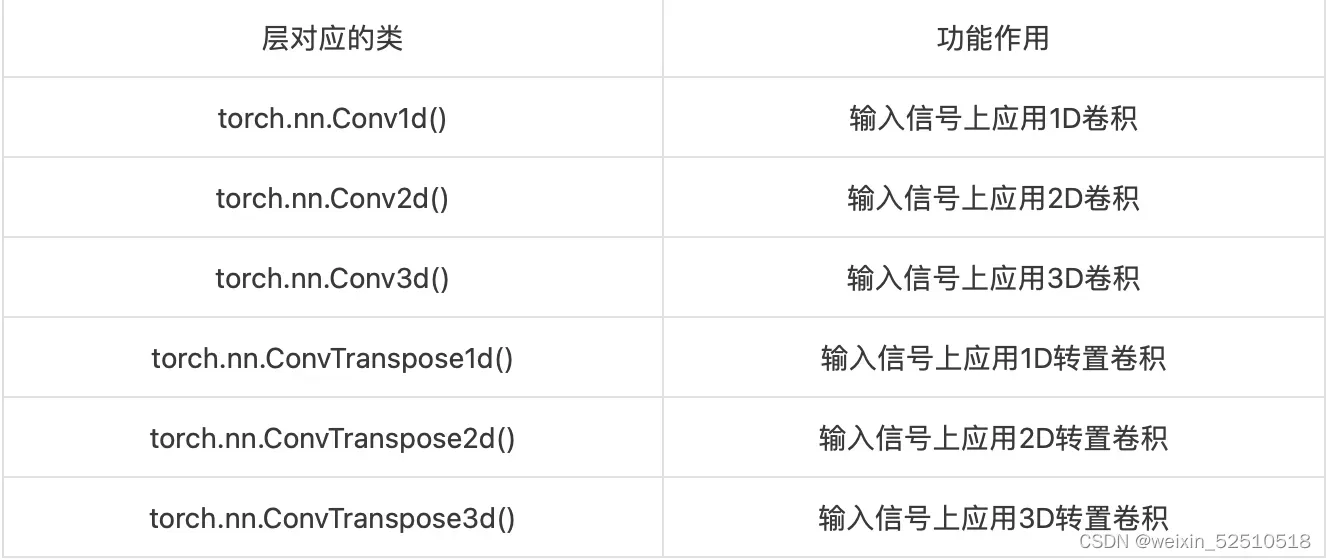
 输入一张图片，来展示经过卷积后，输出特征映射效果

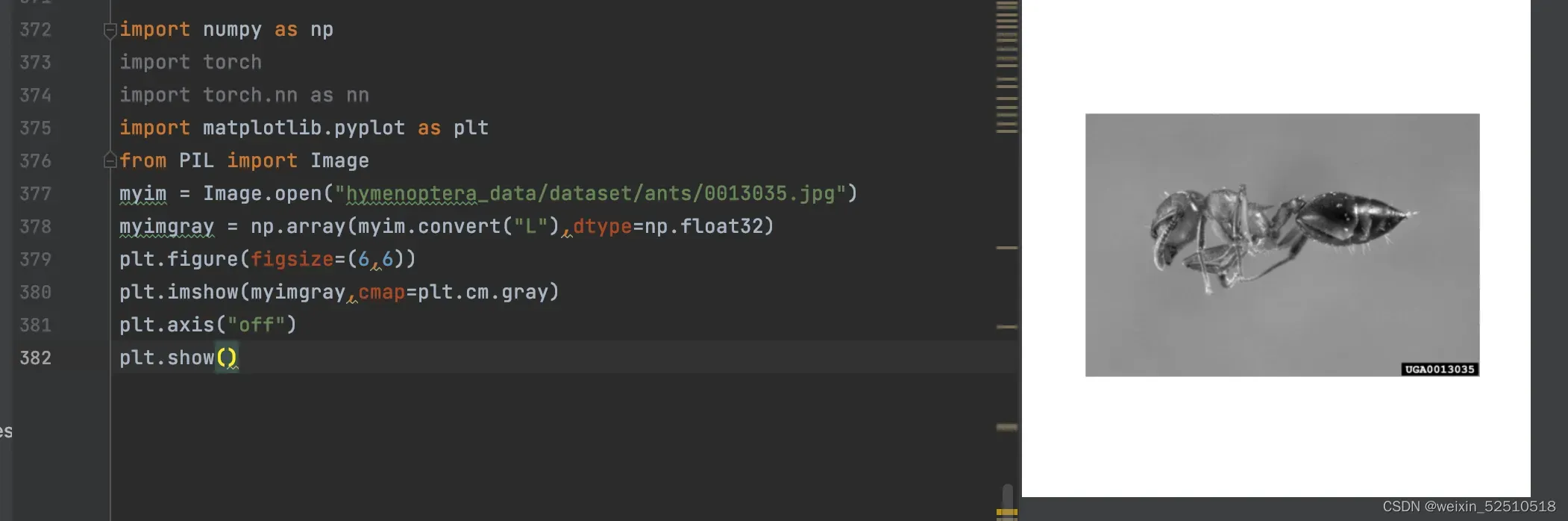
经过上述操作后，得到一个512*768的数组，在使用PyTorch进行卷积操作之前需要将其转化成1*1*512*768的张量

imh,imw = myimgray.shape
myimgray_t = torch.from_numpy(myimgray.reshape(1,1,imh,imw))
print(myimgray_t.shape)

torch.Size([1, 1, 512, 768]) 

卷积时需要将图像转换成四维来表示。对图像进行卷积操作后，获得两个特征映射。

• 第一个特征映射使用轮廓提取卷积核获取
• 第二个特征映射使用卷积核座位随机数，卷积核大小为5*5

kersize  =  5
ker =  torch.ones(kersize,kersize,dtype=torch.float32)*-1
ker[2,2] = 24
ker = ker.reshape((1,1,kersize,kersize))
conv2d = nn.Conv2d(1,2,(kersize,kersize),bias=False)
conv2d.weight.data[0] = ker
imconv2dout = conv2d(myimgray_t)#对灰度图像进行卷积操作
imconv2dout_im = imconv2dout.data.squeeze()#对卷积后的图像进行维度压缩
print("卷积后的尺寸:",imconv2dout_im.shape)
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.imshow(imconv2dout_im[0],cmap=plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(imconv2dout_im[1],cmap=plt.cm.gray)
plt.axis("off")
plt.show()

torch.Size([1, 1, 512, 768])
卷积后的尺寸: torch.Size([2, 508, 764]) 

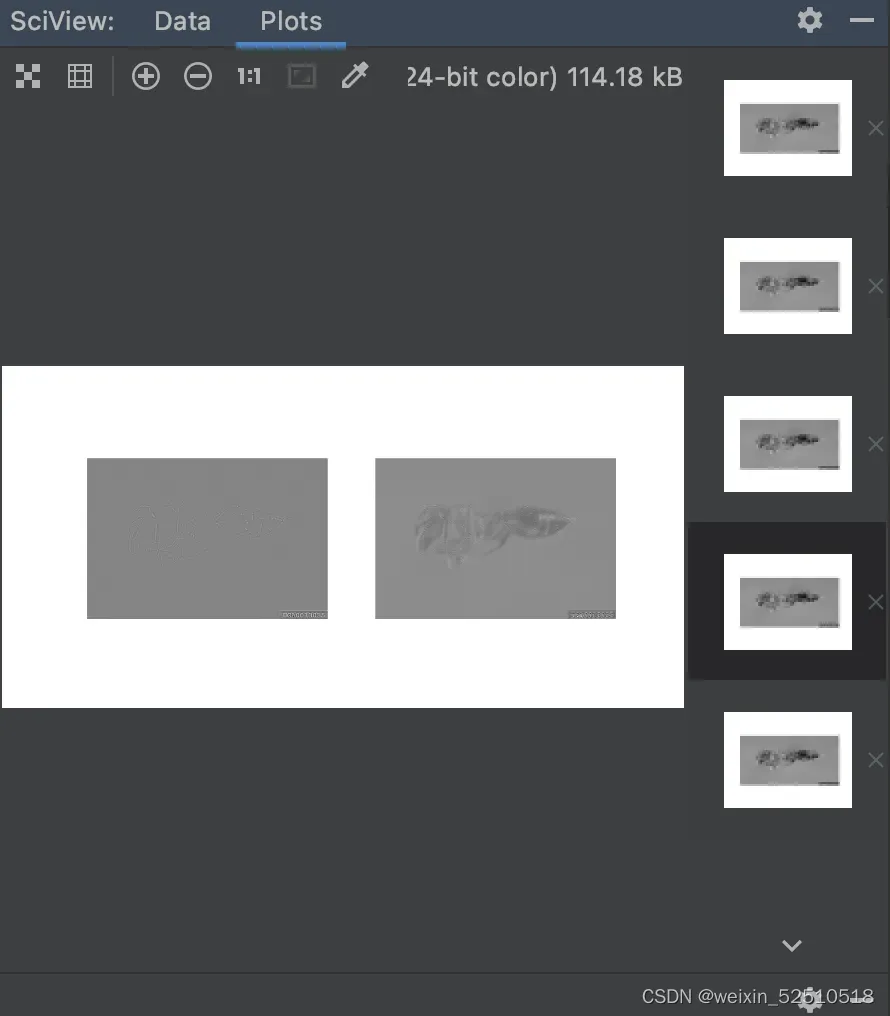
使用边缘特征提取卷积神经核很好地提取出了图像的边缘信息，得到的卷积图像与原始图像很相似。

6.2 池化层

池化操作的一个重要目的是将卷积后得到的特征进行进一步处理(主要是降维)，池化层可以起到对数据进一步浓缩的效果，从而缓解计算时内存的压力。池化会选取一定的大小区域，将该区域的像素使用一个代表元素表示。如果使用平均值代替称为平均值池化，如果使用最大值代替，称为最大值池化。

常用池化操作

​​​​​​​

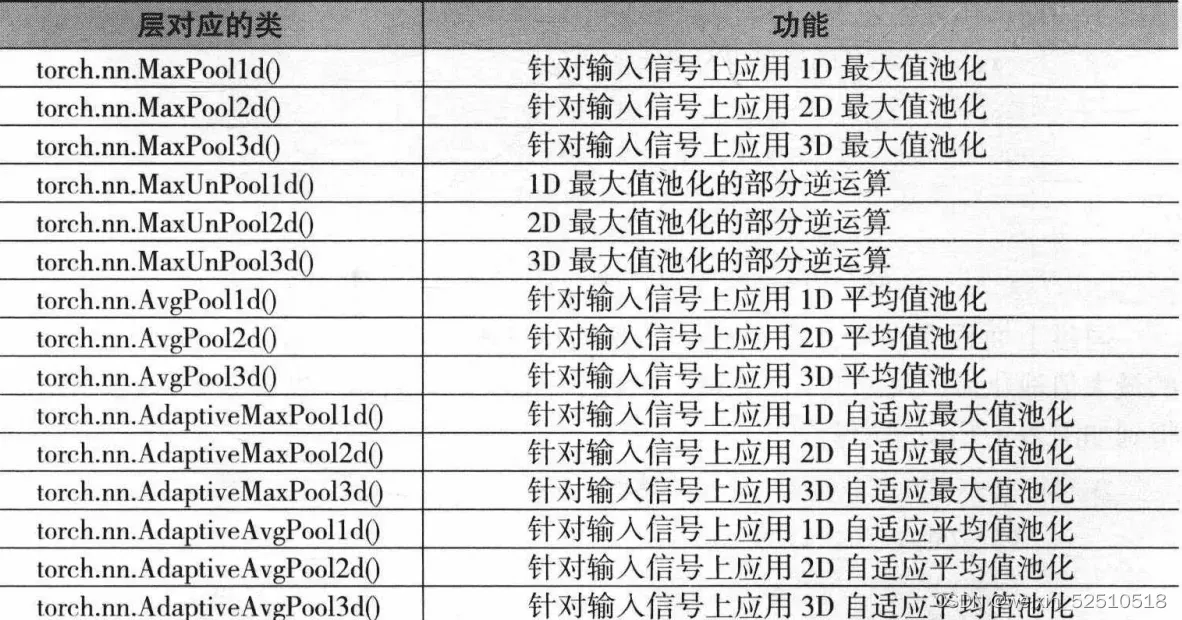
maxpool2 = nn.MaxPool2d(2,stride=2)#对卷积后的结果进行最大值池化
pool2_out = maxpool2(imconv2dout)
pool2_out = pool2_out.squeeze()
print(pool2_out.shape)

torch.Size([2, 254, 382])

#可视化池化后的结果
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.imshow(pool2_out[0].data,cmap = plt.cm.gray)
plt.axis("off")
plt.subplot(pool2_out[1].data,cmap=plt.cm.gray)
plt.axis("off")
plt.show()

同理再使用nn.AdaptiveAvgPool2d()函数，对卷积后的输出进行自适应平均值池化

6.3 激活函数

在PyTorch中，提供了十几种激活函数层所对应的类，最常见的激活函数通常为S型Sigmoid激活函数、双面正切(Tanh)激活函数、线性修正单元(ReLU)激活函数等

6.3.1 Sigmoid激活函数

torch.nn.Sigmoid()对应的Sigmoid激活函数计算方式为

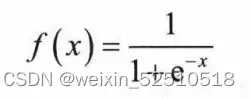
 其输出区间是在(0,1)这个开区间内。该函数在神经网络早期也是常用的激活函数之一 ，但是当输入远离坐标原点时，函数梯度就会变得很小，几乎为0，所以会影响参数的更新速度。

6.3.2 Tanh函数

torch.nn.Tanh()对应的双曲正切函数，计算公式为

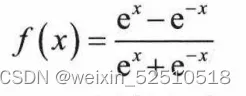
其输出区间是在(-1,1)这个开区间内。整个函数是以0为中心，虽然Tanh函数曲线和Sigmoid函数的曲线形状比较接近，在输入很大或很小时，梯度很小，不利于权重更新，但由于Tanh的取值输出以0对称，使用的效果会比Sigmoid好很多。

6.3.3 ReLU函数

torch.nn.ReLU()对应的ReLU函数又叫做修正线性单元，计算公式为

ReLU函数只保留大于0的输出，其他输出则会设置为0。在输入正数的时候，不存在梯度饱和的问题，计算速度相对于其他类型激活函数要快的多，而且ReLU函数只有线性关系，所以不管是前向传播还是反向传播，速度都很快。

6.3.4  Softplus函数

torch.nn.Softplus对应的平滑近似ReLU的激活函数，其 计算公式为

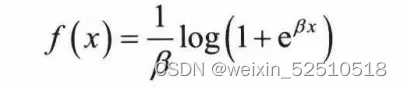
6.3.5 函数的使用 

x = torch.linspace(-6,6,100)
sigmoid = nn.Sigmoid()#Sigmoid激活函数
ysigmoid = sigmoid(x)
tanh = nn.Tanh()#Tanh激活函数
ytanh = tanh(x)
relu = nn.ReLU()#ReLU激活函数
yrelu = relu(x)
softplus = nn.Softplus()#Softplus激活函数
ysoftplus = softplus(x)
plt.figure(figsize=(14,3))#可视化激活函数
plt.subplot(1,4,1)
plt.plot(x.data.numpy(),ysigmoid.data.numpy(),"r-")
plt.title("Sigmoid")
plt.grid()

plt.subplot(1,4,2)
plt.plot(x.data.numpy(),ytanh.data.numpy(),"r-")
plt.title("Tanh")
plt.grid()

plt.subplot(1,4,3)
plt.plot(x.data.numpy(),yrelu.data.numpy(),"r-")
plt.title("ReLU")
plt.grid()

plt.subplot(1,4,4)
plt.plot(x.data.numpy(),ysoftplus.data.numpy(),"r-")
plt.title("Softplus")
plt.grid()
plt.show()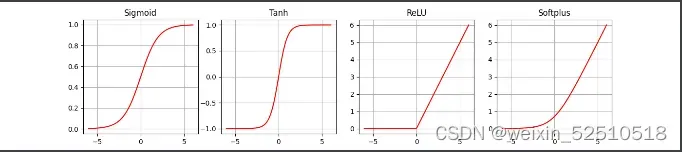

6.4 循环层

在PyTorch提供了三种循环层的实现

以torch.nn.RNN()输入一个多层的Elman RNN进行学习，激活函数使用tanh或ReLU，对于输入序列中的每个元素，RNN每层的计算公式为

 h是时刻的隐状态，x是上一层时刻t的隐状态，或是第一层在时刻t的输入。若nonlineariity=relu。则使用ReLU函数替代tanh函数作为激活函数。

6.5 全连接层

一个由多个神经元组成的层，其所有的输出和该层都有连接，即每个输入都会影响所有神经元的输出。

在PyTorch中的nn.Linear()表示线性变换，全连接层可以看作是nn.Linear()表示线性变层再加上一个激活函数层所构成的架构。

nn.Linear()全连接操作及相关参数如下: 

• in_features 每个输入样本的特征数量
• out_features 每个输出样本的特征数量
• bias 若设置为False,则该层不会学习偏置，默认值为True
• torch.nn.Linear()的输入为(N,in_features)的张量，输出为(N,out_features)的张量

七、数据操作和预处理

PyTorch中torch.utils.data模块包含着一些常用的数据预处理和操作，主要用于读取，切分，准备等。

 7.1 高维数组

在很多情况在，我们需要从文本(csv文件)中读取高维数组的数据，这类数据的特征是每个样本都有很多个预测变量(特征)和一个被预测变量(目标标签)，特征通常是数据变量或者离散变量，被预测变量如果是连续的值，则对应着回归问题的预测，如果是离散问题，则对应分类问题。

7.1.1 回归数据

在使用PyTorch建立模型对数据进行学习时，通常对数据进行预处理，并将他们转化为网格需要的数据形式。

import torch
import torch.utils.data as Data
from sklearn.datasets import load_boston,load_iris
boston_X,boston_Y = load_boston(return_X_y=True)
print("boston_X.dtype:",boston_X.dtype)
print("boston_Y.dtype:",boston_Y.dtype)

boston_X.dtype: float64
boston_Y.dtype: float64

输出的数据集的特征和被预测的变量都是Numpy的64位浮点型数据。而使用PyTorch需要数据应为32位浮点型数据的张量，所以需要将数据集进行转化。

train_xt = torch.from_numpy(boston_X.astype(np.float32))
train_yt = torch.from_numpy(boston_Y.astype(np.float32))
print("train_Xt.dtype:",train_xt.dtype)
print("train_Yt.dtype:",train_yt.dtype)

boston_x.dtype: float32
boston_y.dtype: float32

在训练全连接神经网络时，通常一次使用一个batch的数据进行权重更新，torch.utils.data.DataLoader()函数可以将输入的数据集获得一个加载器，每次迭代可使用一个batch数据。

train_data = Data.TensorDataset(train_xt,train_yt)
train_loader = Data.DataLoader(
dataset = train_data, ## 使用的数据集
batch_size=64, #批处理样本大小
shuffle = True, #每次迭代前打乱数据 
num__workers = 1, #使用两个进程
##检查训练数据集的一个batch的样本的维度是否正确 
for step, (b_x, b_y) in enumerate(train_loader): 
    if step > 0:
        break
##输岀训练图像的尺寸和标签的尺寸及数据类型
print("b_x.shape:",b_x.shape)
print("b_y.shape:",b_y.shape) 
print("b_x.dtype:”,b_x.dtype)
print("b_y.dtype:",b_y.dtype)

b_x.shape: torch.Size([64, 13])
b_y.shape: torch.Size([64])
b_x.dtype: torch.float32
b_y.dtype: torch.float32

 先使用Data.TensorDataset()。将训练数据X和Y放在一起组成 数据train_data,然后使用Data.DataLoader()定义一个数据加载器，每64个样本为一 个batch,最后使用for循环获得一次加载器的输出内容b_x和b_y,它们均为torch的 32位浮点型张量。

7.1.2 分类数据准备

分类数据和回归数据的不同点在于，分类数据的被预测变量为离散类别变量, 所以在使用PyTorch定义的网格模型时，默认的预测标签事64位有符号的整型数据。

iris_x, irisy = load_iris (return__X_y=True)
print("iris_x.dtype: ", iris_x.dtype)
print("irisy:",irisy.dtype)

iris_x.dtype: float64

irisy: int64

上面程序，读取数据，然后查看数据的特征和标签的数据类型。

train_xt = torch. from__numpy (iris_x.astype (np.float32))
train_yt = torch.from_numpy(irisy.astype(np.int64))
print ("ntrain_xt.dtype: ", train_xt.dtype)
print ("train_yt.dtype:", train_yt.dtype)

 train_xt.dtype: torch.float32
 train_yt.dtype: torch.int64

准备好数据类型后，再使用Data.TensorDataset()和Data.DatalLoader()定义数据的加载器

train_data = Data.TensorDataset(train_xt,train_yt)#将训练集转化为张量后，使用TensorDataset将X和Y整理到一起
train_loader = Data.DataLoader( #定欠一个数据加载器，将训练数据集进行批量处理
    dataset=train_data,
    batch_size=10,
    shuffle=True,
    num_workers=1,
)
##检查训练数据集的一个batch样本的维度是否正确
for step, (b_x, b_y) in enumerate(train_loader):
    if step > 0:
        break
##输出训练图像的尺寸和标签的尺寸与数据类型
print ("b_x. shape: ", b_x.shape)
print ("b_y. shape: ", b_y.shape)
print ("b_x. dtype: ",b_x.dtype)
print ("b_y. dtype:", b_y.dtype)

b__x.shape: torch.Size ([10, 4])
b_y.shape: torch.Size([10])
b_x.dtype: torch.float32
b__y.dtype: torch.int64 

从输出可知，每个batch使用了十个样本数据，并且数据的类型已经正确转化 

7.2 图像数据

torchvision中的datasets模块包含多种常用的分类数据集下载及导入函数，可以 很方便地导入数据以及验证所建立的模型效果。

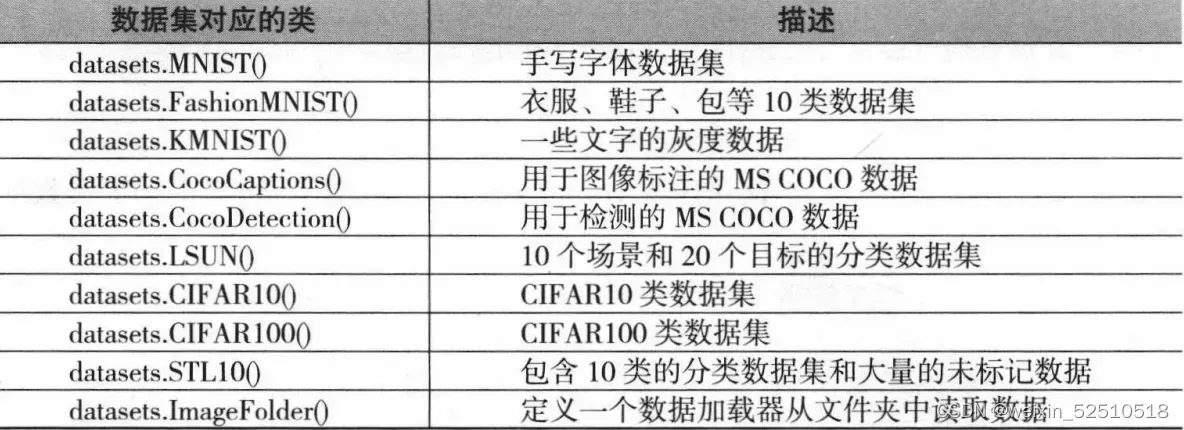
torchvision中的transforms模块可以针对每张图像进行预处理操作

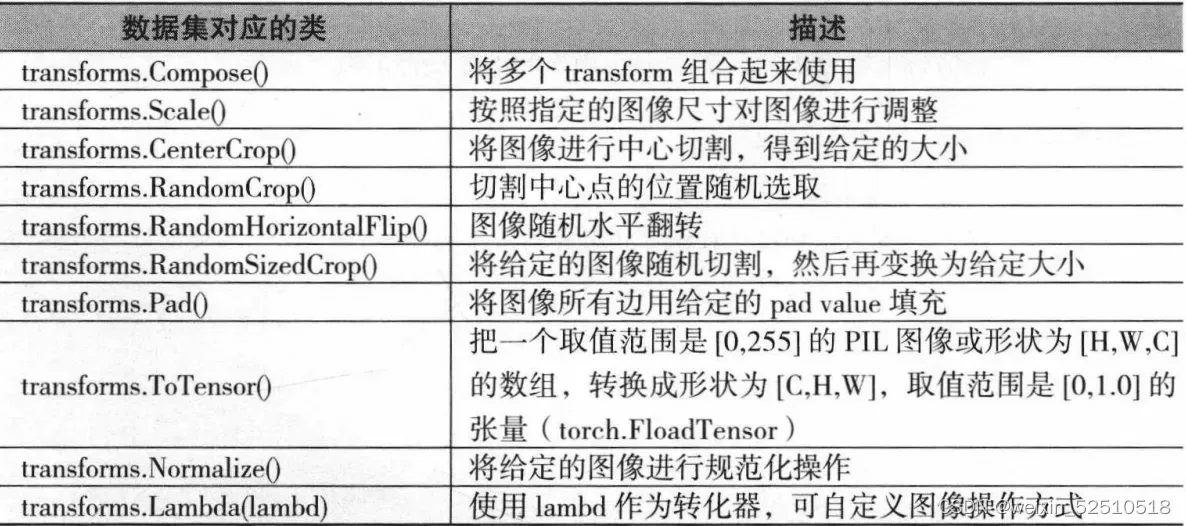
 以实际的数据集为例，结合torchvision中的相关模块的使用，展示图 像数据的预处理操作。

• 一种是从torchvision中的datasets模块中导入数据并预处理,
• 另一种是从文件夹中导入数据并进行预处理。