一、麻雀搜索算法SSA

二、小波神经网络WNN
WNN是一种以小波基函数为隐含层节点、激励函数误差反向传播的神经网络,如下图所示:
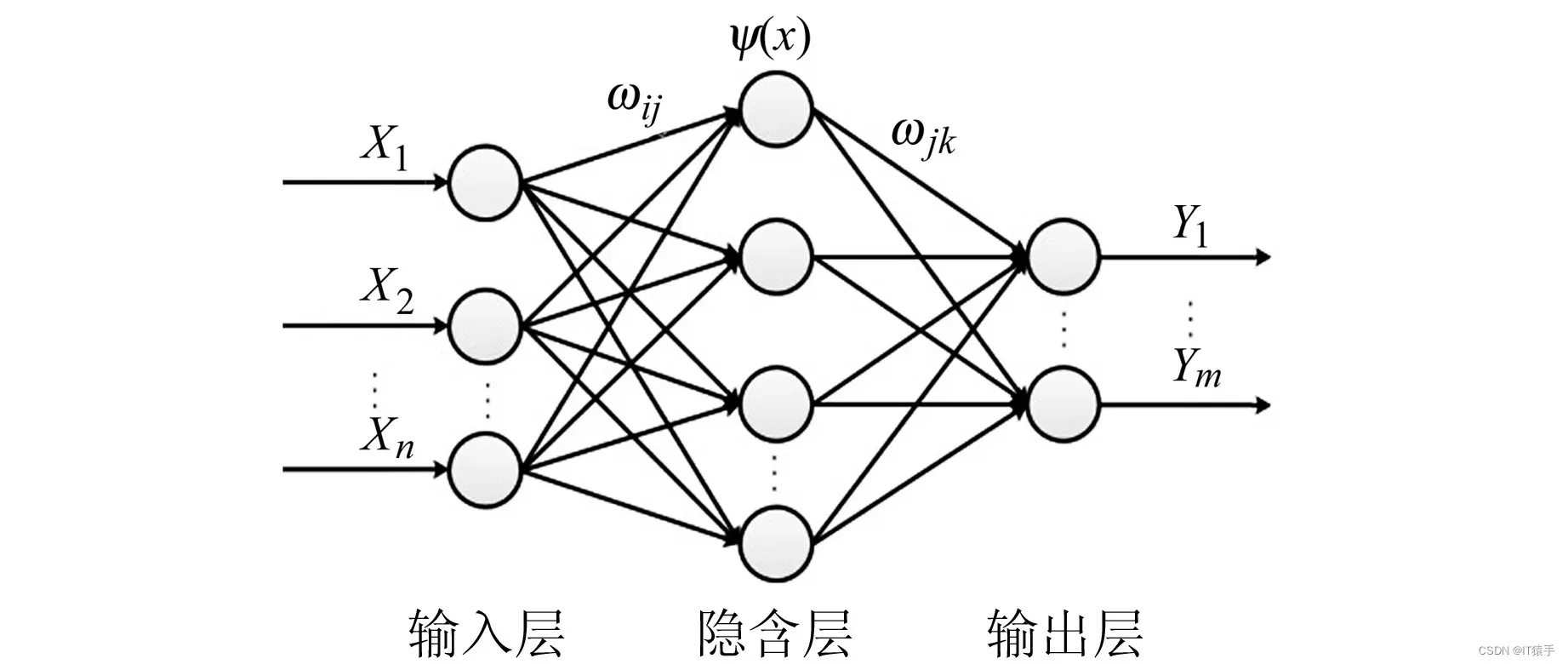
图中X为WNN的输入样本,Y为WNN的预测输出,ωij和ωjk分别为连接输入层与隐含层、隐含层与输出层的权值,ψ(x)为小波基函数。本文所采用的小波基函数为Morlet小波函数,其表达式为:

参考文献:钱建国,樊意广.基于改进小波神经网络的GPS高程拟合研究[J].大地测量与地球动力学,2022,42(03):253-257.DOI:10.14075/j.jgg.2022.03.007.
三、数值实验
小波神经网络WNN中待优化参数为:输入层与隐含层的权值、小波基函数的伸缩因子、小波基函数的平移因子、隐含层与输出层的权值。麻雀搜索算法SSA的个体由WNN中输入层与隐含层的权值、小波基函数的伸缩因子、小波基函数的平移因子、隐含层与输出层的权值构成,目标函数为真实值与预测值的均方误差MSE。构建结构为5-8-2的小波神经网络WNN,通过SSA优化WNN结构参数,使其MSE最小。
部分数据如下:前5列为输入,后2列为输出
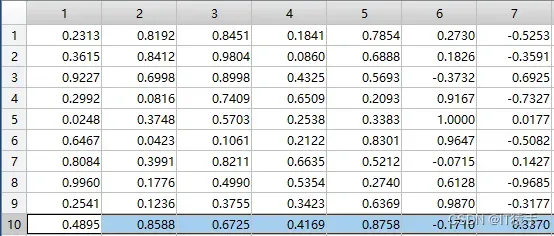
部分代码如下:WNN隐藏层神经元个数可以自己修改
close all
clear
clc
global inputnum hiddennum outputnum TrainNum
inputnum=5;%神经网络输入层神经元个数(输入样本维度)
hiddennum=8;%神经网络隐藏层神经元个数(可以自己修改)
outputnum=2;%神经网络输出层神经元个数(输出样本维度)
TrainNum=100;%训练集数目
%% 麻雀搜索算法SSA优化小波神经网络WNN,目标函数是均方误差MSE
SearchAgents_no=50; % 种群大小(可以修改)
Function_name='F1';
Max_iteration=1000; % 最大迭代次数(可以修改)
[lb,ub,dim,fobj]=fun_info(Function_name);% 在fun_info.m中可以查看上下限及目标函数
[fMin,bestX,SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); %bestX是WNN的最优参数
save bestX bestX %保留SSA优化WNN得到的最佳参数
%%
save SSA_curve SSA_curve %保留曲线
%% 画出SSA优化WNN的均方误差随迭代次数的图
figure
semilogy(SSA_curve,'Color','g')
title('Objective space')
xlabel('Iteration');
ylabel('MSE');
%axis tight
grid on
box on
legend('SSA')
%%
display(['The best solution obtained by SSA is : ', num2str(bestX)]);
display(['The best optimal value of the objective funciton found by SSA is : ', num2str(fMin)]);
SSA求解结果如下:
MSE收敛图:
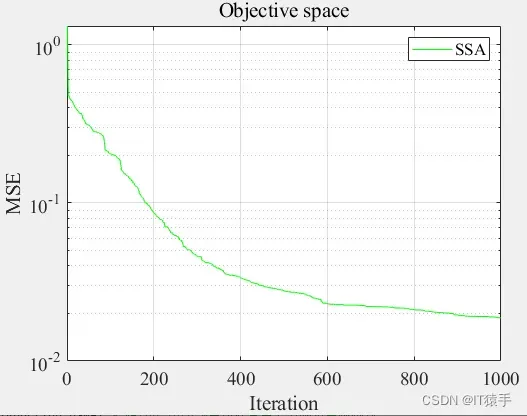
两个目标真实值与预测值:红色为真实值,蓝色为预测值,真实值与预测值用黑线连接,一一对应。
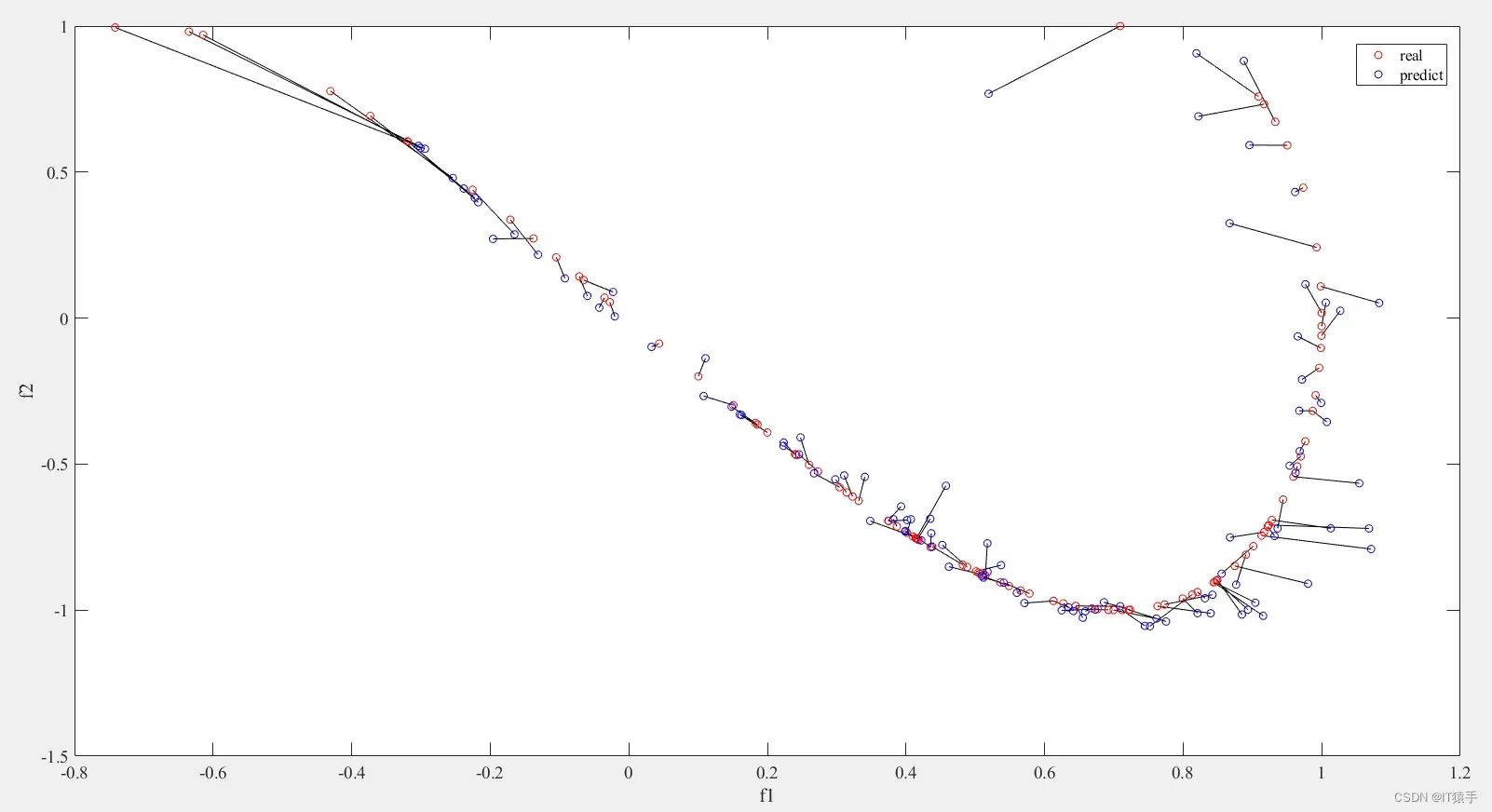
目标1真实值与预测值:
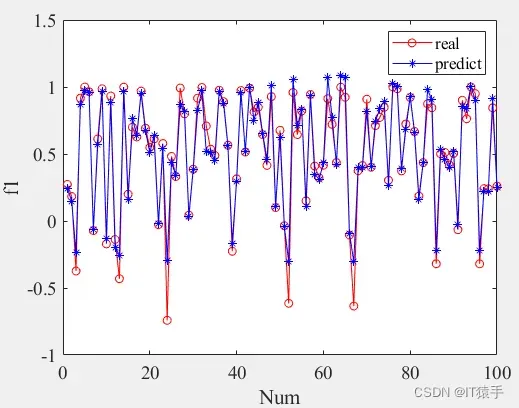
目标2真实值与预测值:
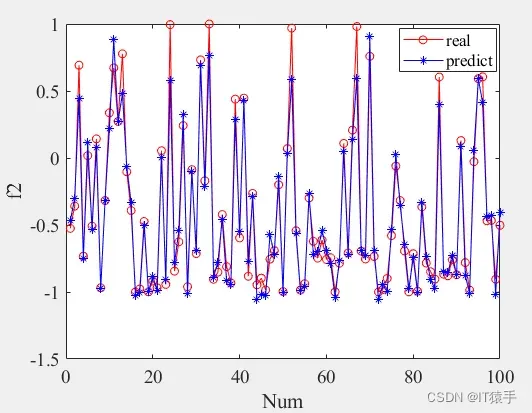
两个目标真实值与预测值的绝对误差MAE:
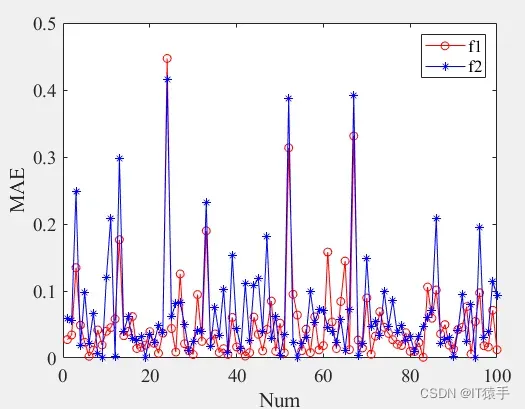
由此可见SSA优化WNN用于数据预测效果十分不错,设置合适的隐藏层神经元个数,加大种群规模和迭代次数效果更佳。
四、参考代码
参考代码见评论区或添加博主微信获取。
文章出处登录后可见!
已经登录?立即刷新
