0-R(Zero-R)
- 0-R 是一种常用的 baseline，是通过对样本集合进行统计，然后选用出现频率最高的样本类作为对所有测试集样本预测的结果。例如一个数据集包含三类样本，标签分别是 A：1000个, B：500个, C：500个. 那么这个时候最多类是 A，占比是 50% ，因此对于任何测试样本，这个 0-R 模型的预测结果都是 A，而这个模型的正确率也就是 50%
- 0-R 模型不涉及任何特征的使用
- 只有 majority class 对于预测样本类别有用
1-R(one-R)
- 只使用一组特征来构建模型并预测标签。
- 步骤如下：
-
对于每个特征：
- 针对每个特征中 所有不同的取值，计算这个取值的弱势标签数
- 将所有取值的 弱势标签数求和，除以所有的样本数，得到以这个特征构建0-R 时候的错误概率
-
比对每个特征的结果并选出拥有最高分类概率的特征作为标准，在测试集中进行样本预测。
-
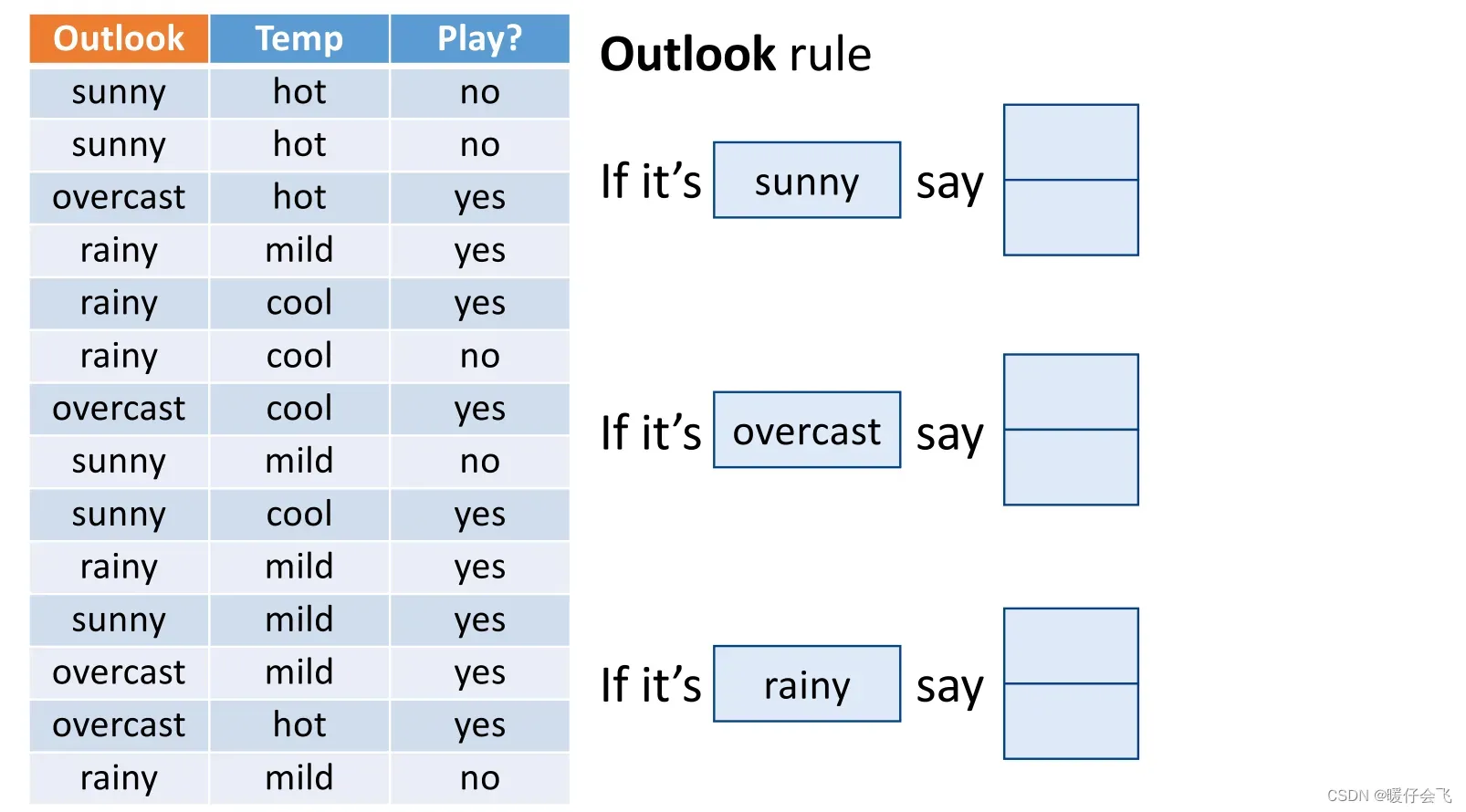
- 例如下面对 outlook 这个特征进行构建 1-R 模型
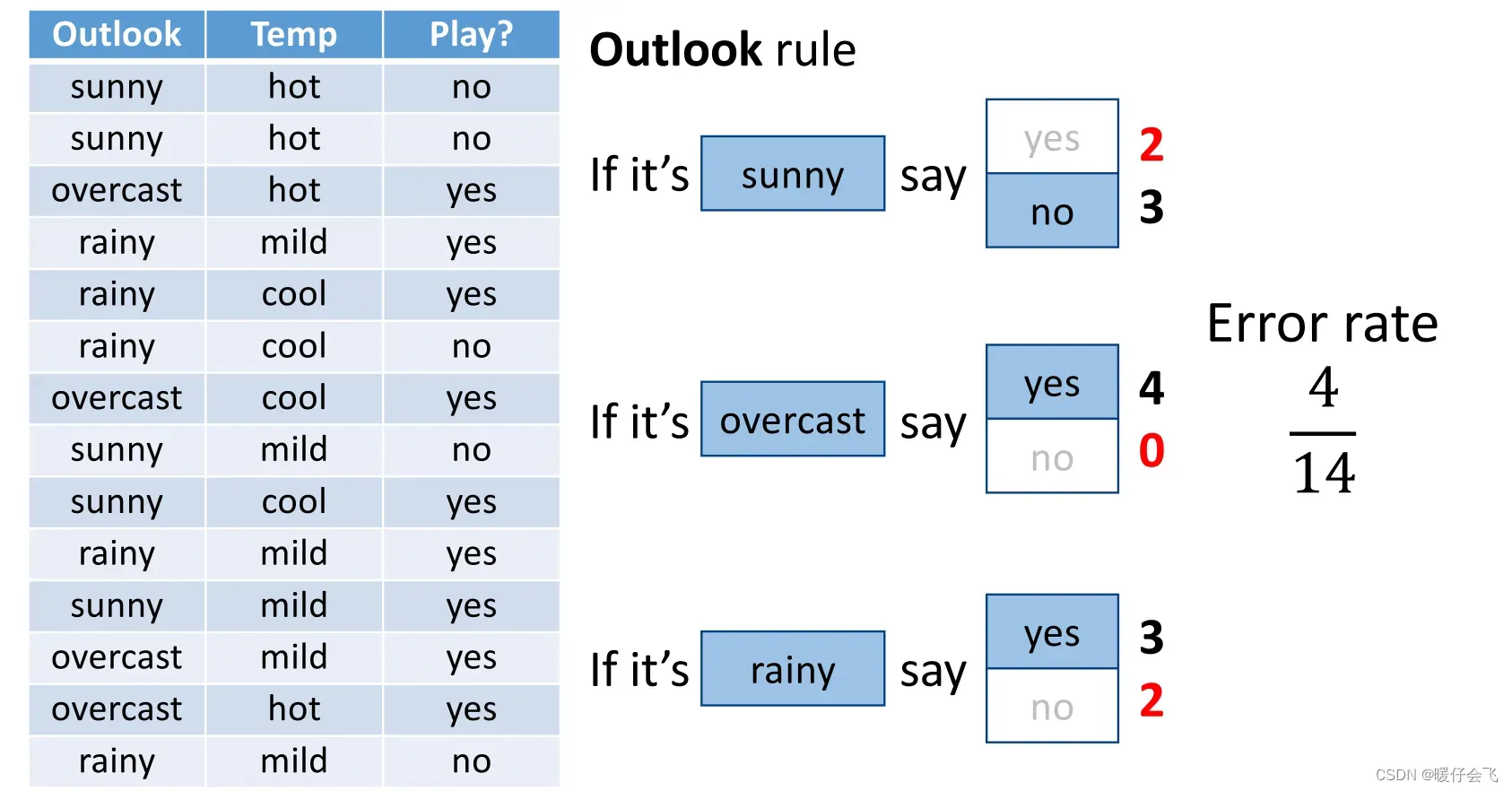
- sunny 中对于 no 和 yes 的数量分别是 2，3；所以对于 sunny 来说，把 no 标签看做是优势标签，而 yes 标签被认为是弱势标签，因此 sunny 的错误样本数是 2 个
- 同样的方式我们可以得到 outlook 中其他所有的值（sunny，overcast， rainy）对于标签的错误样本数，分别是 2个，0个，2 个，所以整个 outlook 特征对于标签的错误率是
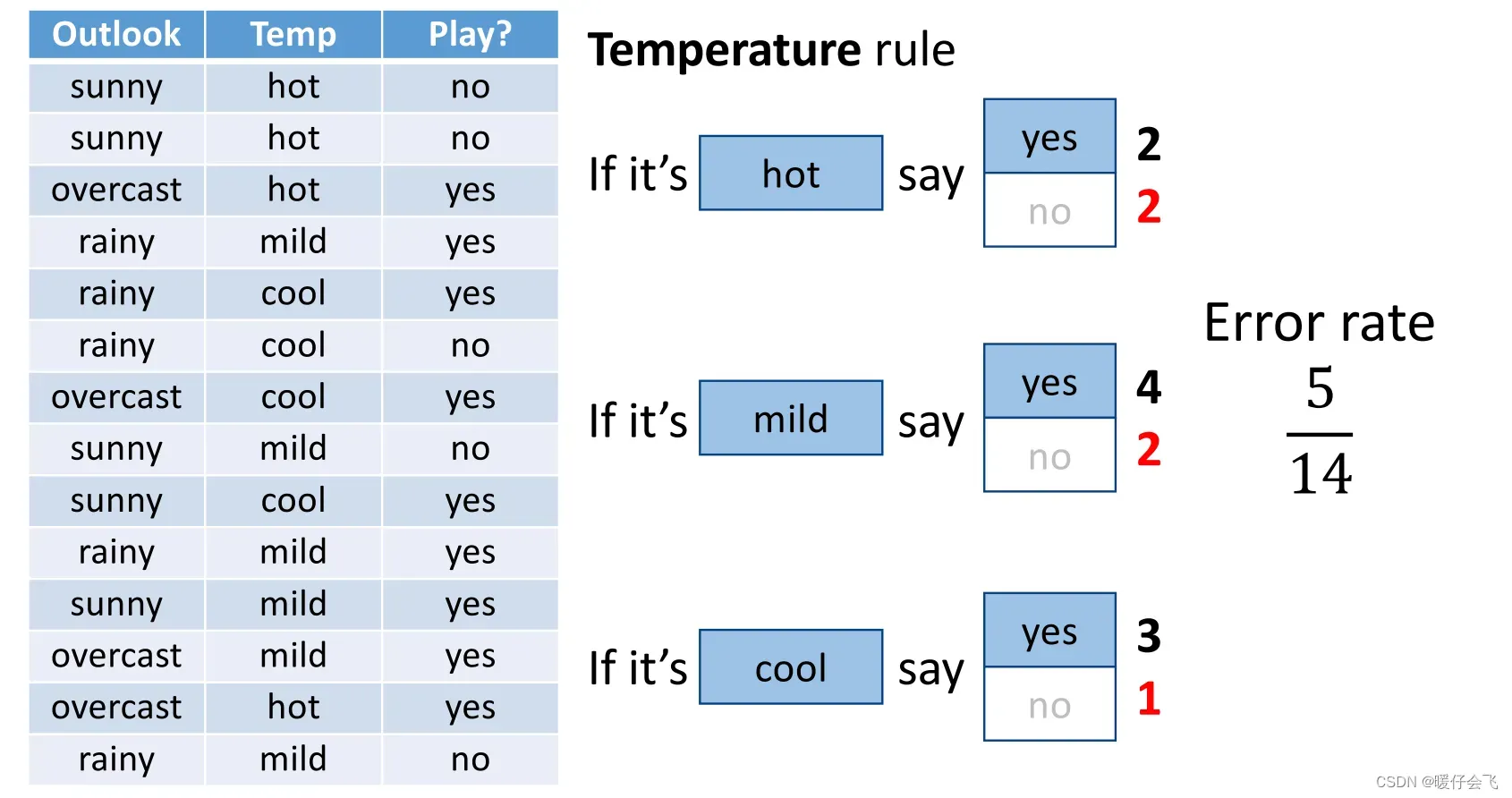
- 对其他所有的特征计算错误率：
图中得到 Temp 特征对于标签的错误率是
- 对于整个数据集采用 1-R 的方式计算所有特征的错误率：
- 因此我们把 1-R 称为决策树桩（decision stump）
因为通过 1-R 可以选出决策树的根节点（根特征）
从 1-R 到决策树
- 如果首先根据上面 1-R 决定一个 树桩 outlook 作为决策树的根，构建决策树：
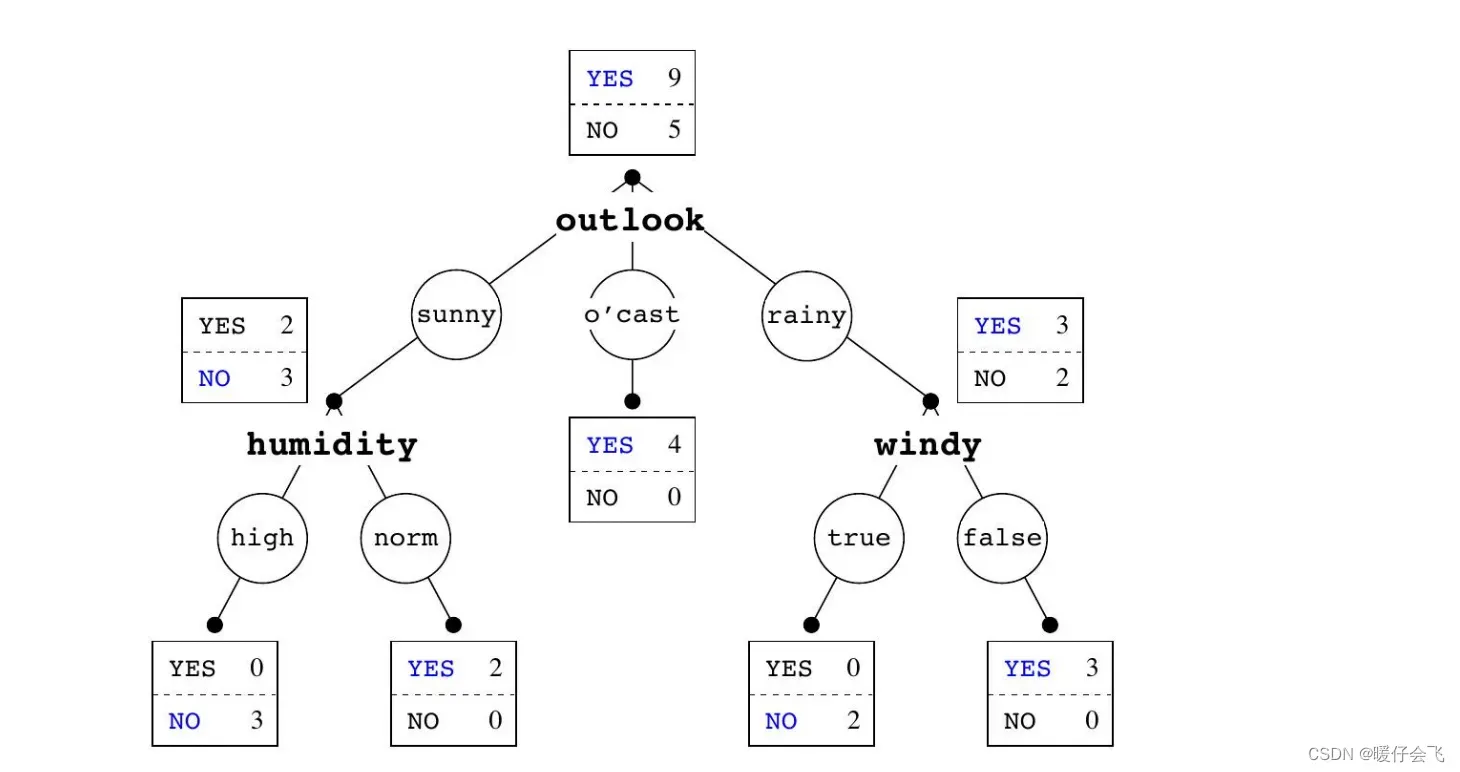
- 对于 overcast 这个叶子节点来说，已经不存在错误样本（yes=4，no=0）；因此它不再需要通过其他特征来降低错误样本数。
- 而对于 sunny（错误样本 2 个）和 windy（错误样本 2 个）则需要根据当前的特征集再选出额外的特征来使得错误率减小。
- 举个例子：
假设将
的所有样本这个当做一个新的数据集，那么这个数据集包含了 5 个样本，从剩下的所有特征
中选出一个特征来构造 1-R 模型，使得当前情况下能够有最小的错误率。
- 从上图中可以看出，基于
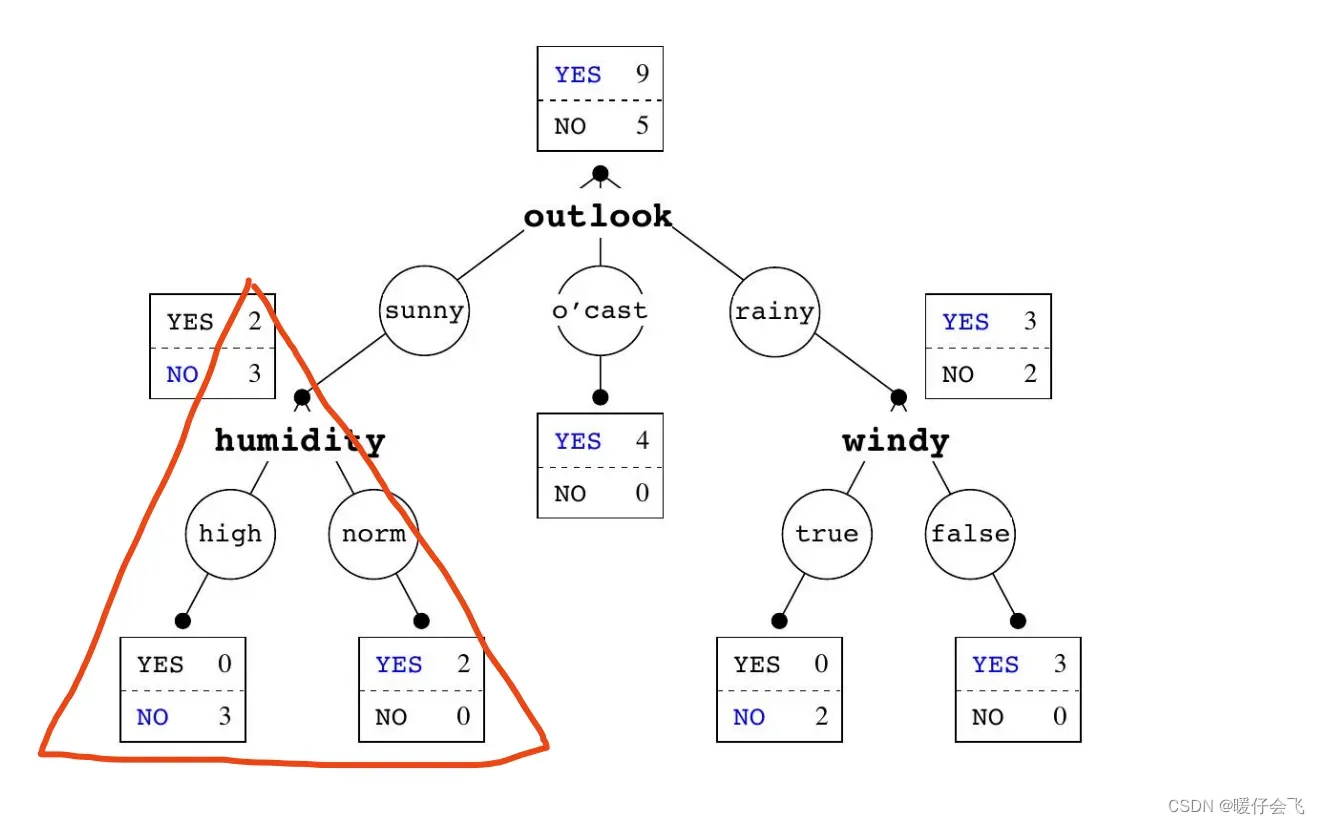
- 同样的操作也发生在
的所有样本中，
- 基于这些样本，选用 windy 特征来构建 1-R，得到错误率也降低到 0
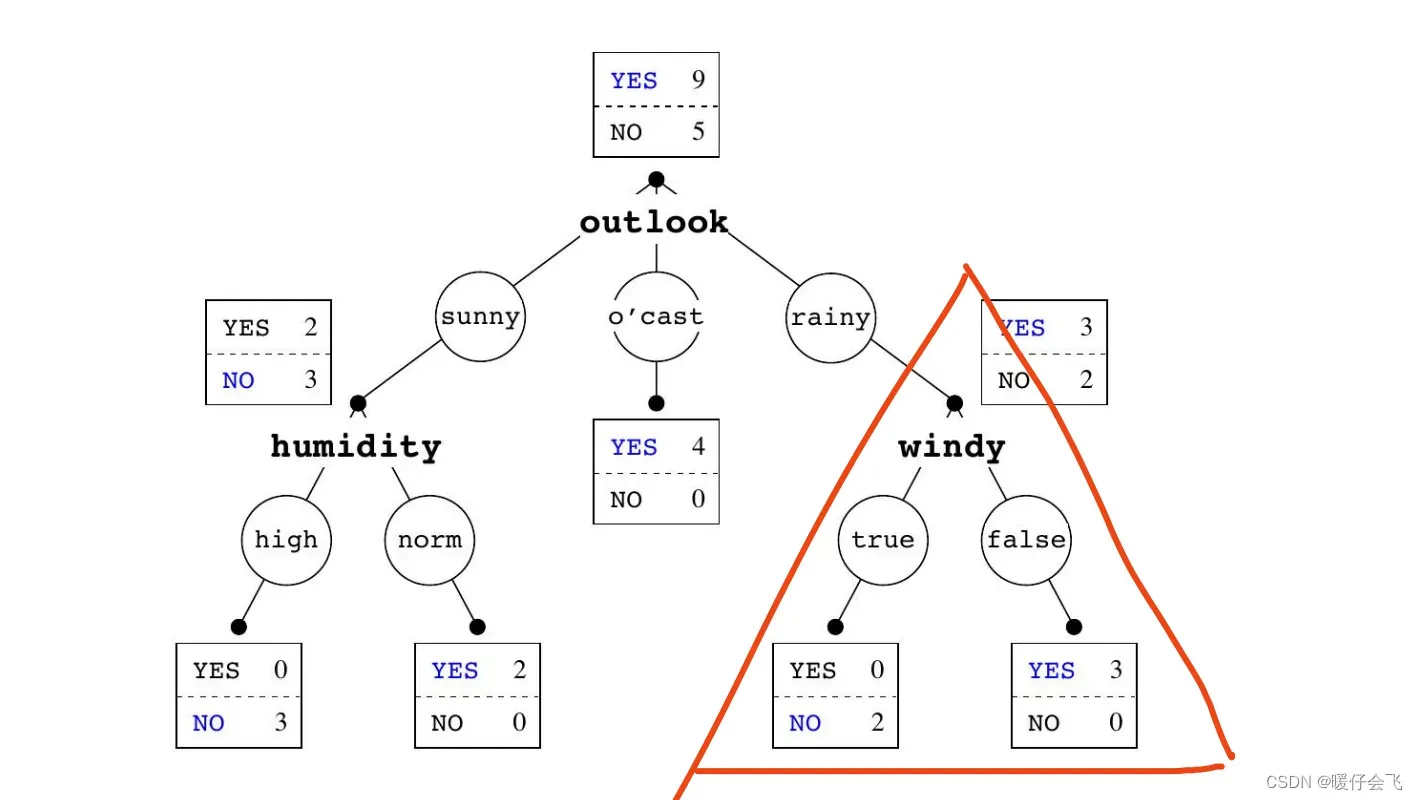
- 所以从总体上来看，这棵树所有的叶子结点是没有错误样本的，也就是说这棵树是一棵完美的决策树了。
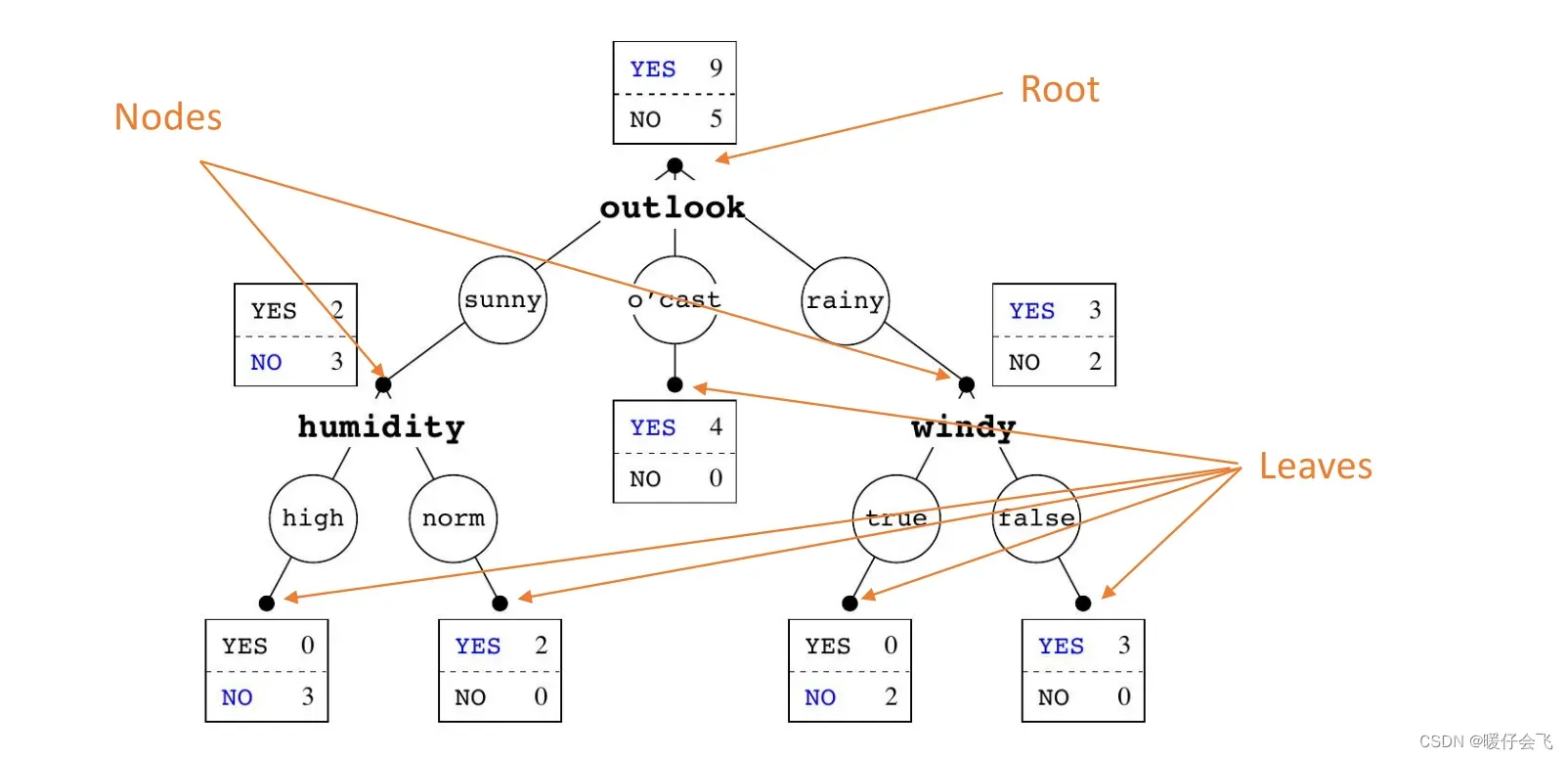
ID-3决策树
- 从上一个部分我们也可以看到构建一棵决策树的步骤，是递归的，从根节点开始分支，每个叶子节点都会有一定量的样本，如果这个叶子的样本中没有错误样本（优势样本比例 100%）那么我们就不再对这个叶子进行分支；
- 而如果叶子节点的样本中有错误样本，那么我们就把这个叶子节点中的所有样本当做一个子数据集 subset，并从未使用过的特征中选择一个新的特征基于 subset 构建一棵子树（上文中的 humidity 和 windy 子树）
- ID-3 算法如下：
- Note： 实际上叶子节点的错误率为 0 是很苛刻的条件，因此我们通常会使用一个阈值来决定是否要继续分支。而且我们通常不采用 1-R 的方式作为决策树分支的标准。
决策树的分支条件——不纯度
- 我们在 1-R 到决策树 中对决策树进行继续分支，依靠的是某个叶子节点依然存在 “错误样本” 也就是说只要这个节点依然存在“错误样本” 我们就进行分支，我们认为这种叶子节点是 “不纯” ，那么如何衡量一个叶子节点 “不纯” 的程度呢？
- 为了更好的决定一个叶子节点是否需要继续分支，我们引入 不纯度 来决定。当叶子节点的不纯度超过了某一个 阈值 我们认为这个叶子节点是不可忍受的，必须进行分支来降低错误率。
Entropy
- 熵是用来衡量 “不可预测性” 的一个指标，结果的不确定性越大， 熵就越大。
- 给定一个概率分布，预测一个事件所需的信息(以比特为单位)就是该分布的熵或信息值（information value）
- 公式定义：
- 定义：
假设对于某个节点，使用 entropy 计算不纯度
- 假设如果现在的分支标准是 不纯度 > 0.45 那么上面的节点就不需要再分支了。
决策树的特征选择——信息增益
- 当决策树根据 entropy衡量出结点不纯度高于设定的阈值，这时候决策树要进行分支，那么如何选择合适的特征进行分支呢？
- 在基于 1-R 策略构成的决策树中，分支选用的新特征的标准就是：选用的特征让当前叶子结点分支后的 错误率 最小。
- 除了这种选择特征的方式，我们还可以用信息增益和信息增益比来选择特征。
信息增益（Information Gain）
- 特征 A 的信息增益是下面两部分的差值：
- 在选用特征 A 进行当前结点
分支之前，这个叶子结点的 entropy
- 选用 A 特征完成分支之后，
的 entropy 的加权平均值（mean information）
- 在选用特征 A 进行当前结点
- 这两部分的差值叫做信息增益，它反映的是选用 A 对于原本叶子结点
- Note： 信息增益的计算是在每个结点进行分支的时候，对于当前结点的所有备选特征进行 IG 的计算，而不是在一开始就计算好。
- 也就是说，当我在考虑
平均信息（mean information）
-
对于结点
进行分支，分支后的平均信息量根据下面公式计算：
-
是分支产生的某个新结点
上的信息量 entropy
-
每个新结点也可以看成是特征
-
是这个新结点中样本的数量
占分支之前的结点
的比例：
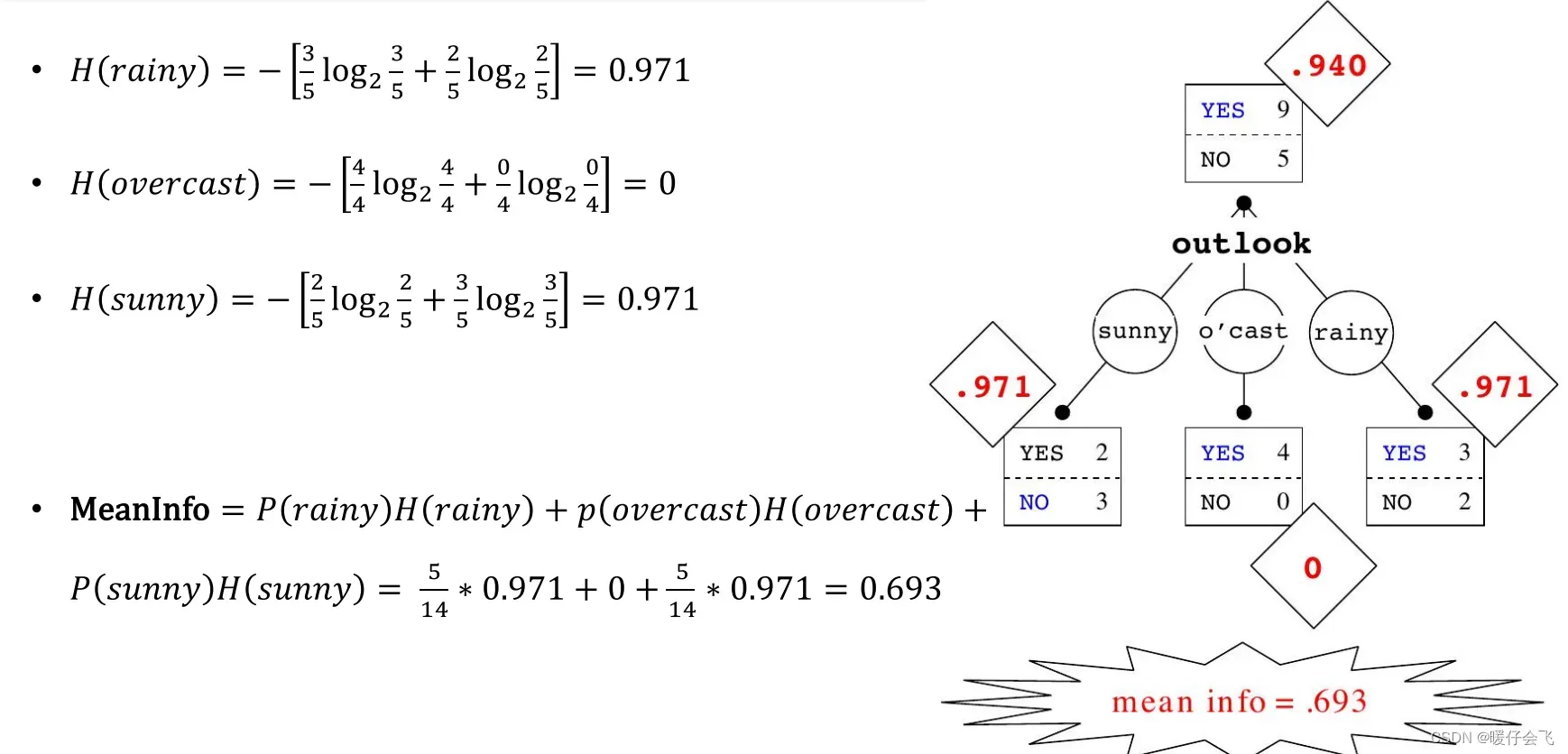
- 下图中，新结点
分别是
- 分支后每个新结点的 entropy 分别是下图中计算的
- 所以最终得出的 MI = 0.693
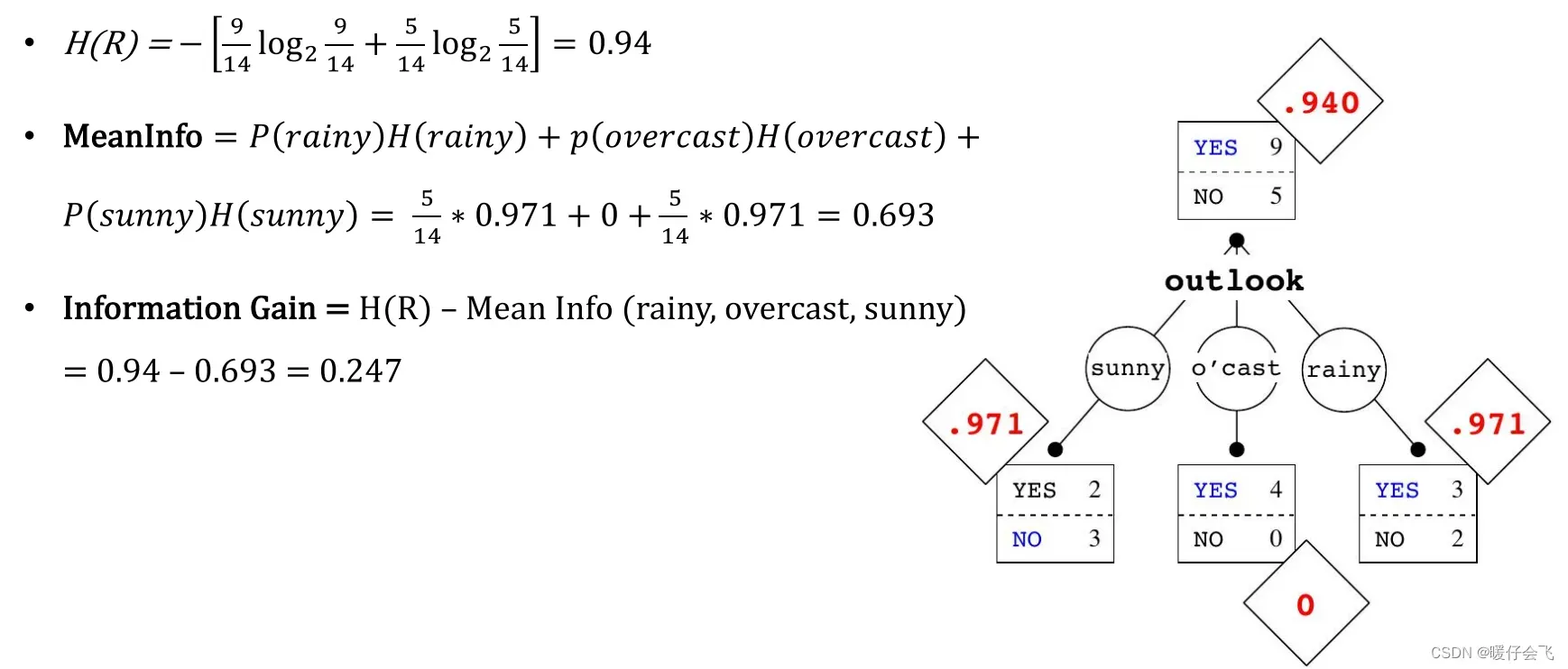
- 分支之前的结点的 entropy =
- 因此在当前结点选择 outlook 特征进行分支的信息增益比是：
- 通过这种方式，可以计算出在当前结点所有可用特征的信息增益，然后选出 IG 最大的特征作为当前结点的 分支特征。
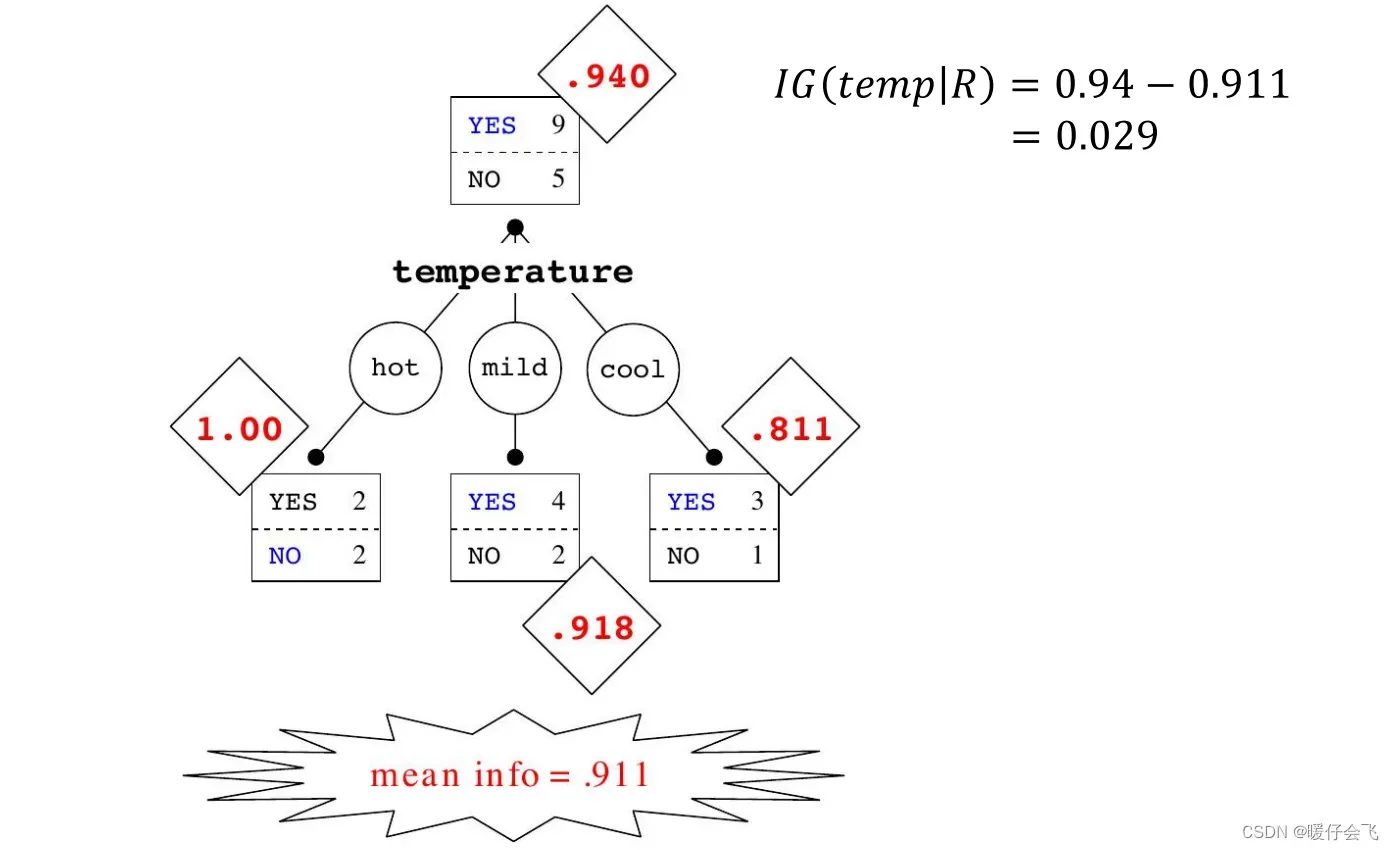
- 按照同样的方式，我们可以算出在某个结点所有可选特征的信息增益：
- 综上来看，还是 outlook 的信息增益最大，因此在当前结点，我们选择 outlook 作为新的特征来构建分支。
信息增益的缺陷（shortcoming of IG）
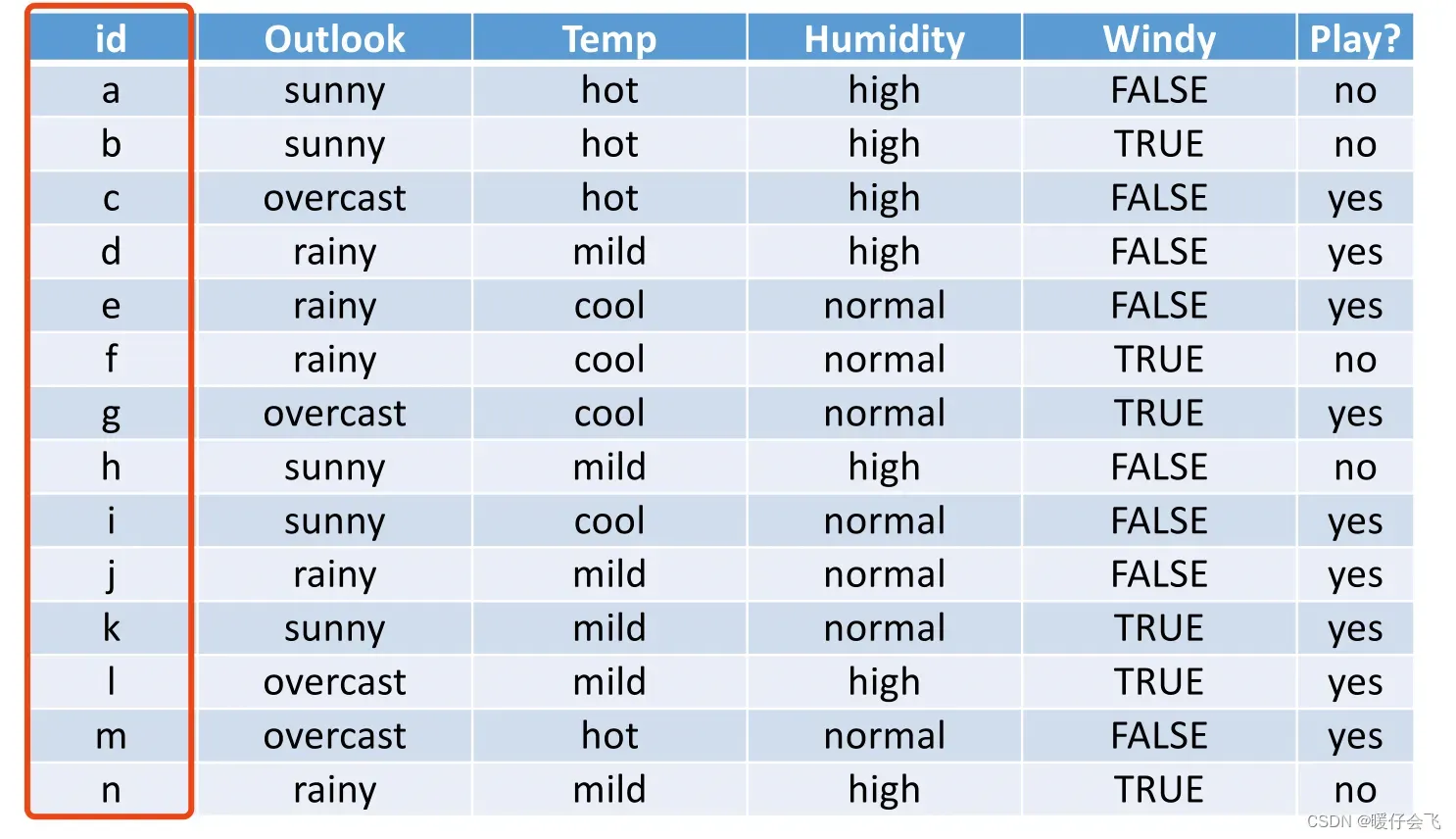
- 如果拿 id 作为特征来计算信息增益，我们可以得到什么结果呢？
- 信息增益竟然是 0.94，之所以这样是因为 id 的个数和样本个数一样多，因此以 id 特征进行分支，分出来的叶子节点数量也会和样本数一样多，那也就根本不存在 劣势样本 所以每个结点的纯度都是 100%。
- 这也体现出信息增益作为特征筛选标准的一个问题，那就是对于类似于 id 的这种特征（特征内的取值非常多）是不起作用的。而且容易导致整个决策树模型 过拟合
- 为了解决这个问题，我们采用更加合理的信息增益比（gain ration）作为分支特征筛选的标准。
分离信息 (Split Information)
- 每个 特征 的熵称为 split information，是衡量一个特征内部的混乱度的指标。我们在上面提到的熵指的是整个数据集中标签类（class） 的熵。
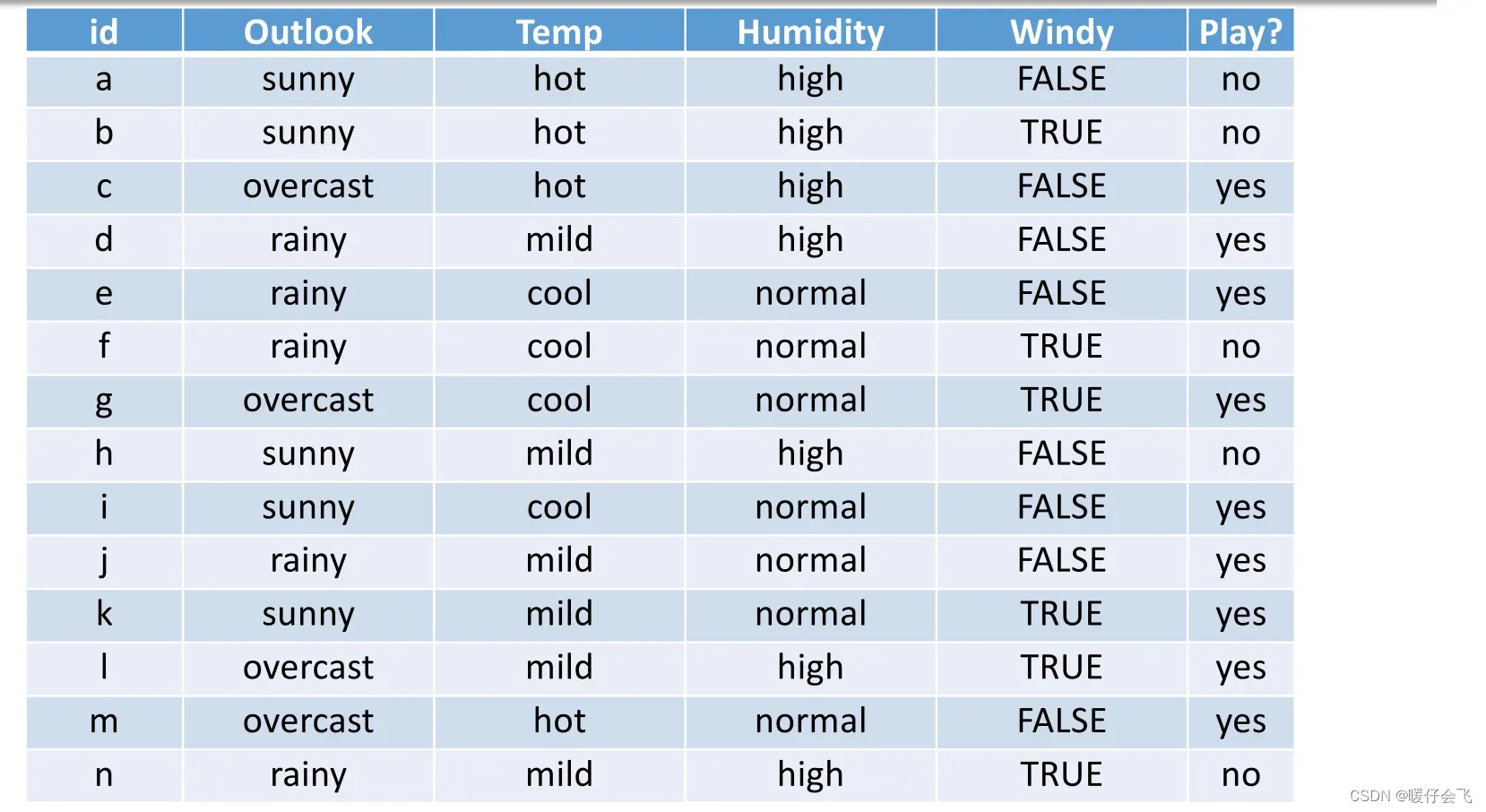
- 通过一个具体的例子来展示基于 特征 的熵，和基于 class 的熵有什么不同：
- 在下面的例子中，YES, NO 是类别标签，因此如果我们求类别标签的混乱度也就是 H® 我们会使用
- 其中
是不同类别的个数，
是第
类标签的样本所占的比例
- 但是在算特征的 split info 的时候我们使用：
信息增益比（Gain Ratio）
-
通过对分支信息增益的 规范化 减小 “分支过多” 造成的偏差
-
GR 的公式如下：
-
是进行分支的新特征；
是分支之前的原本节点
-
不鼓励选择具有许多均匀分布值的特征
-
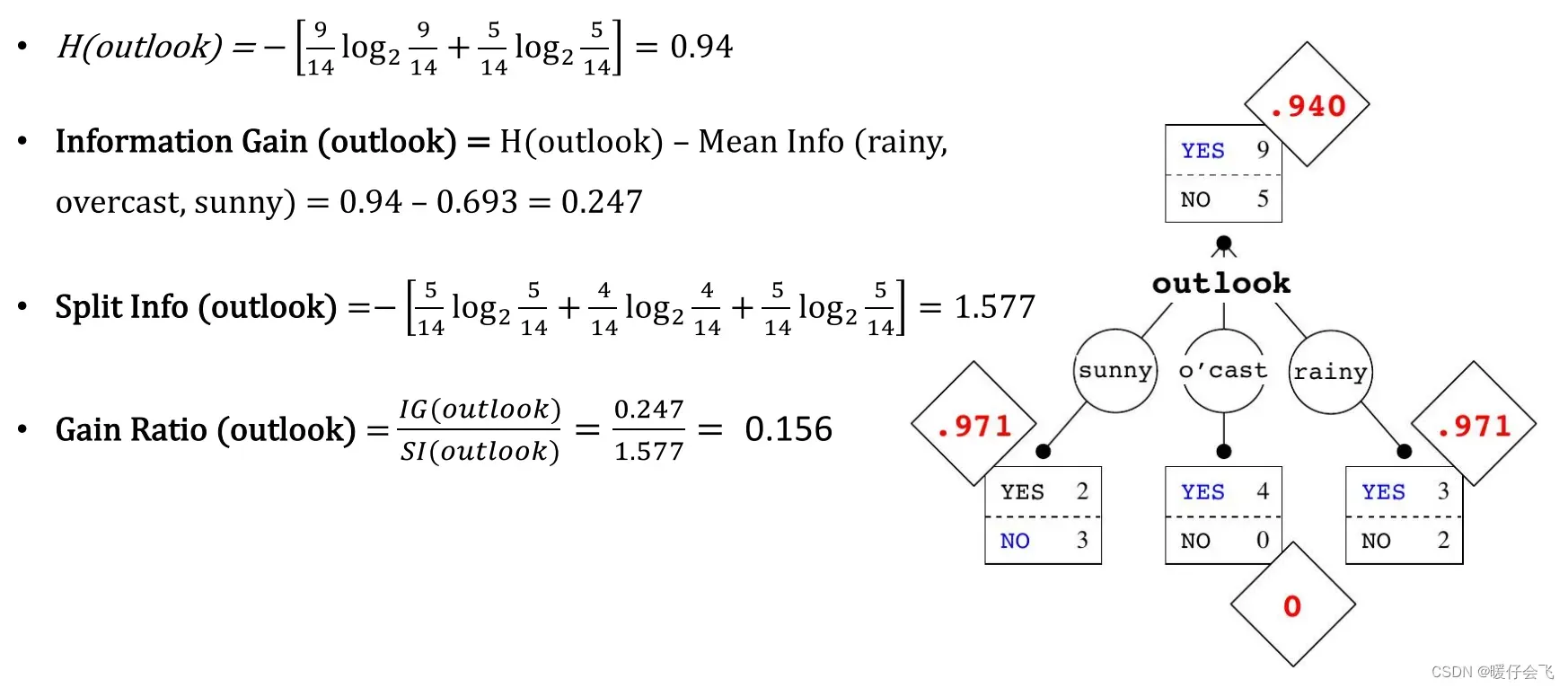
一方面信息增益比可以延续信息增益的效果对继续分支的特征进行筛选
-
另一方面可以避免一个特征中的取值情况过多而导致的信息增益偏差
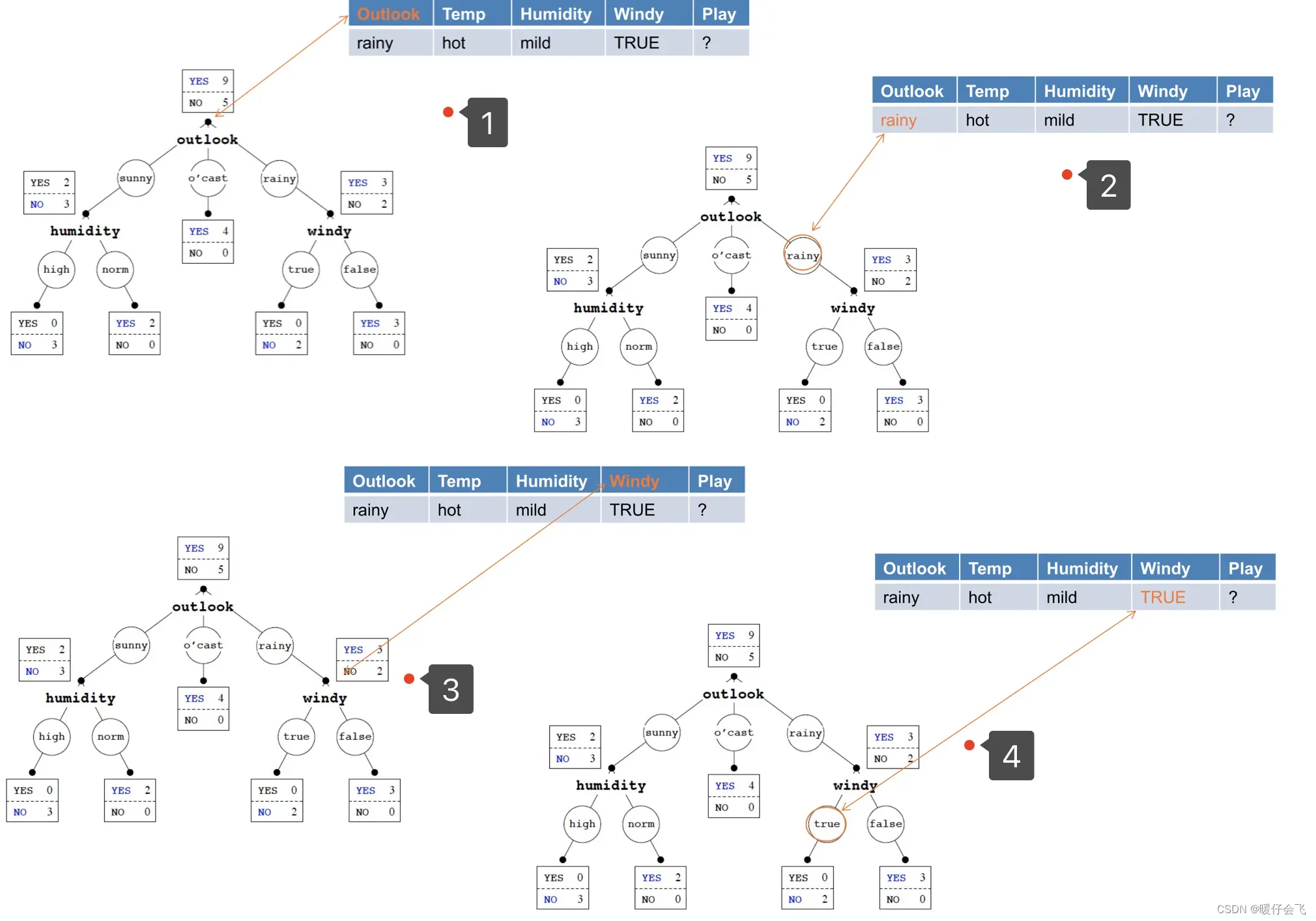
决策树对于样本的预测
- 假设目前已经形成了一棵不错的决策树
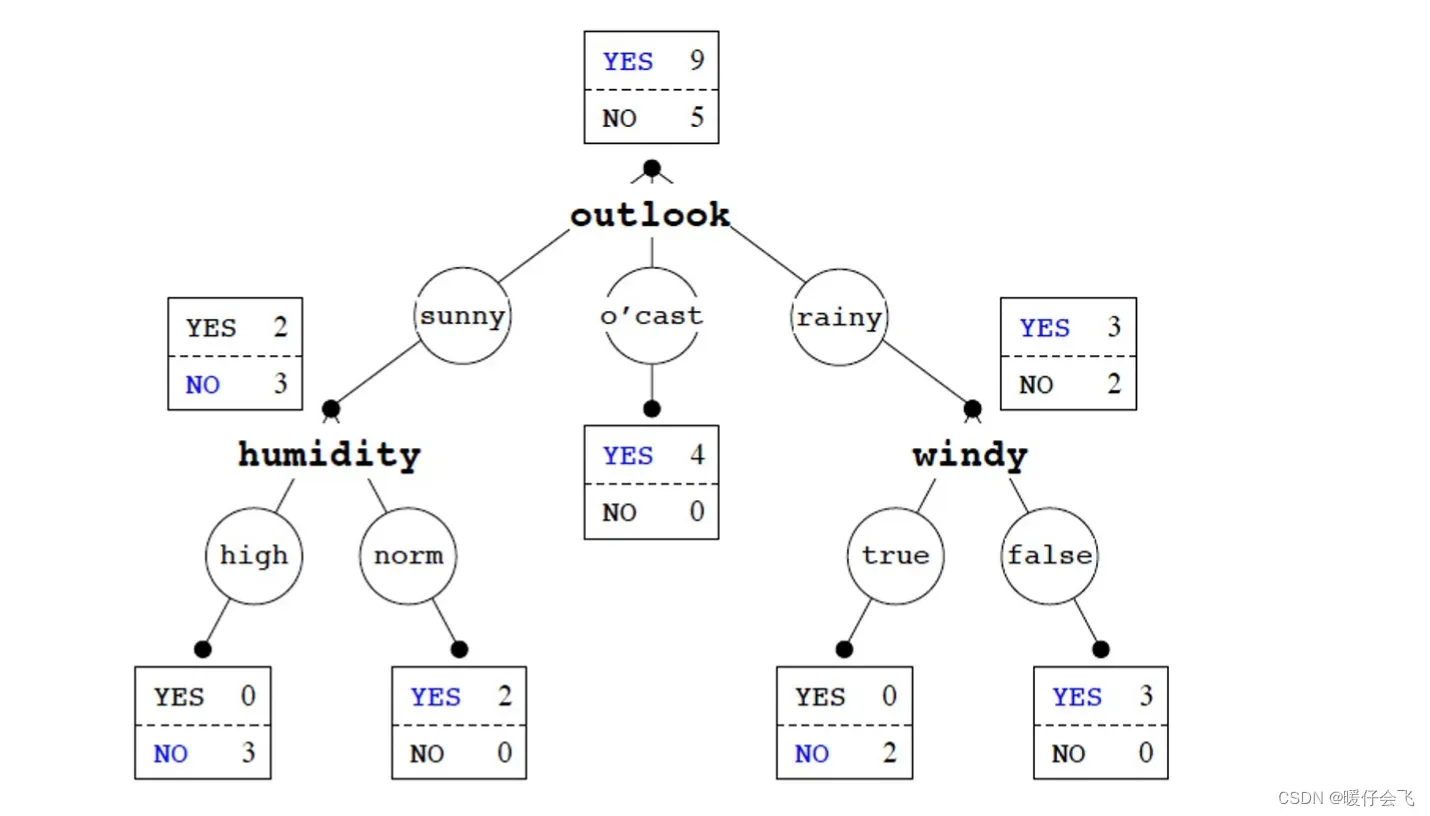
见过的样本
- 对于一个曾经见过的特征组合，我们可以根据决策树的分支策略对测试的样本进行预测：
未见过的特征
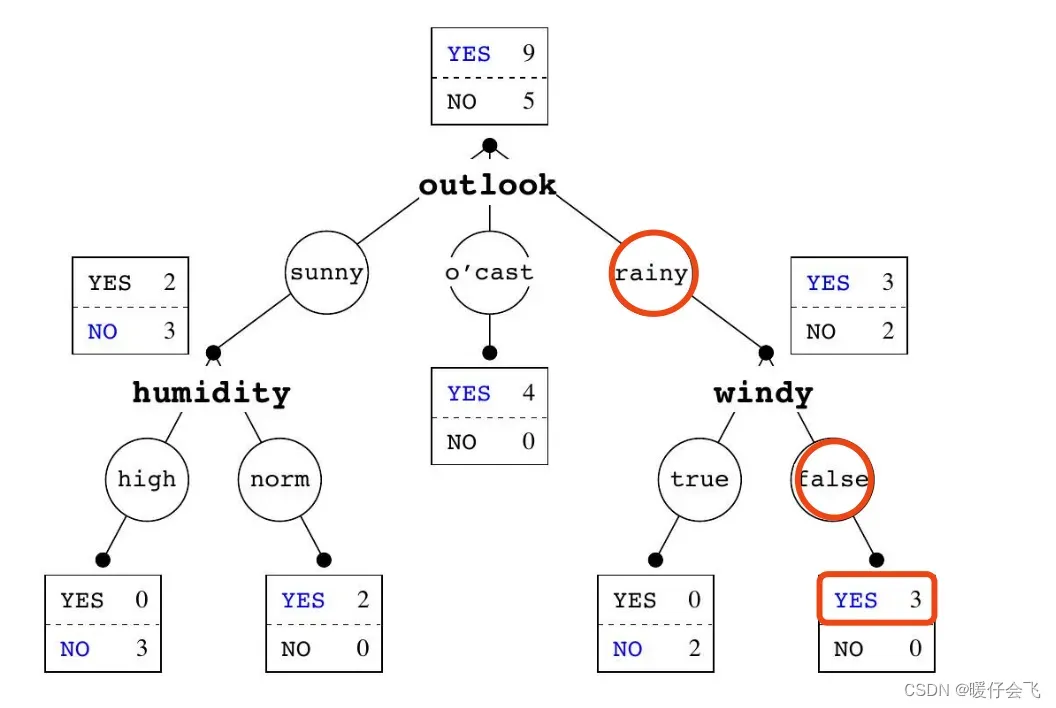
- 如果一个样本不能够符合分支的情况，应该怎么进行决策呢？例如
- 这时候决策树会先匹配 rainy，进入右边的分支
- 然后根据 test 中发现 windy 是 false 所以他会给出 yes 的答案（因为 yes 在 windy=false 中是优势类）
决策树的深度 & 性能
- 相比于深层的决策树，我们更希望能够得到较浅的决策树；因为使用的特征过多代表决策树的过拟合风险太大。
关于ID-3决策树的讨论
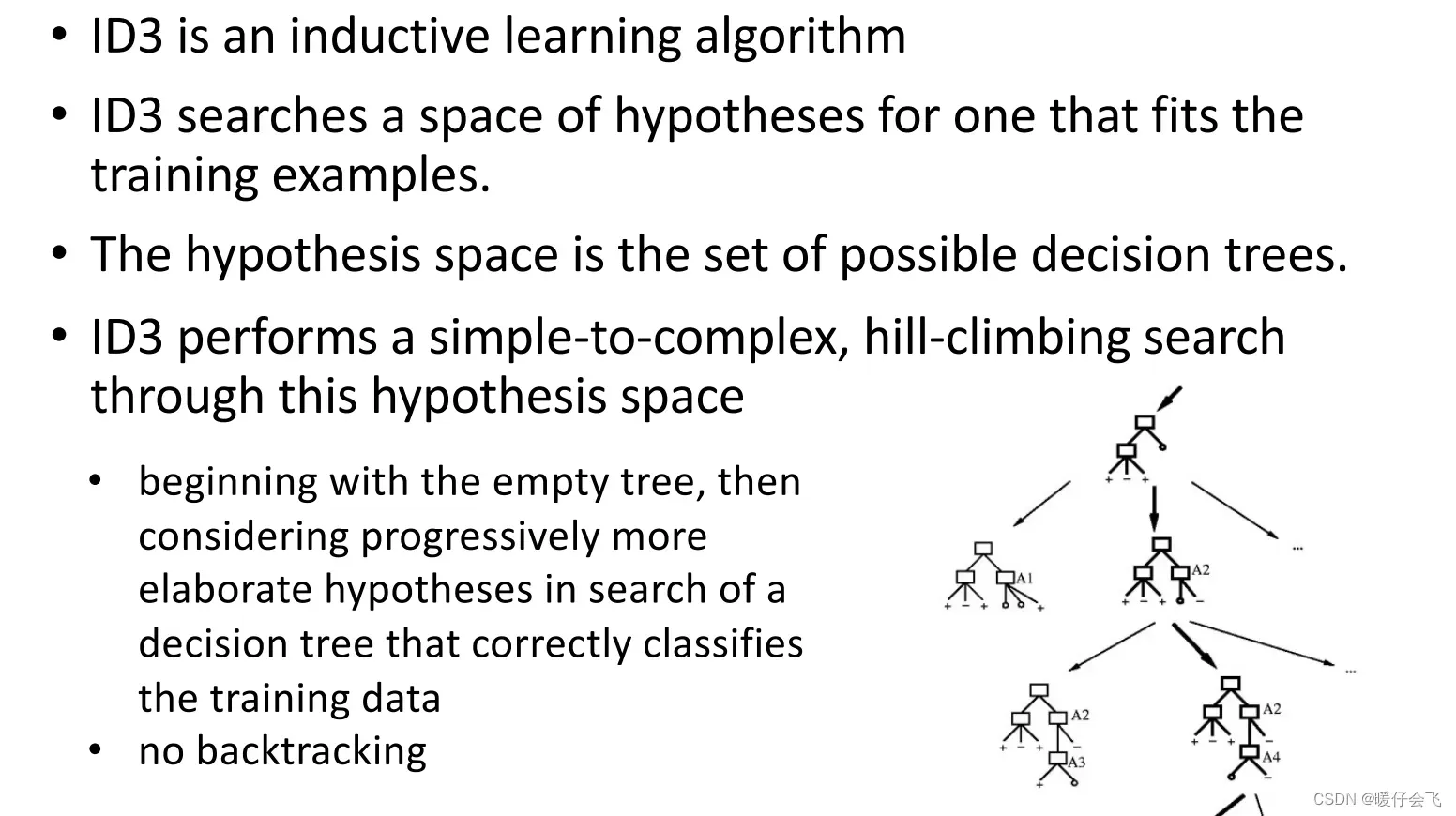
- ID-3 是一种归纳学习算法
- ID-3在假设空间（hypothesis space）中搜索符合训练示例的假设
- 假设空间是可能决策树的集合
- ID3在这个假设空间中执行从简单到复杂的爬山搜索
- 从 empty tree 开始，然后在寻找正确分类训练数据的决策树时逐步考虑更详细的假设
- 不使用回溯
- 我们倾向于构造更浅的树
ID-3 的优点
- 训练和分类非常快速
- 高可解释性
ID-3 的缺点
- 容易过拟合
- 容易受不相关特征的影响
- 偏爱 nomial 类型的特征
文章出处登录后可见！
已经登录？立即刷新
