1. 运动学模型线性化

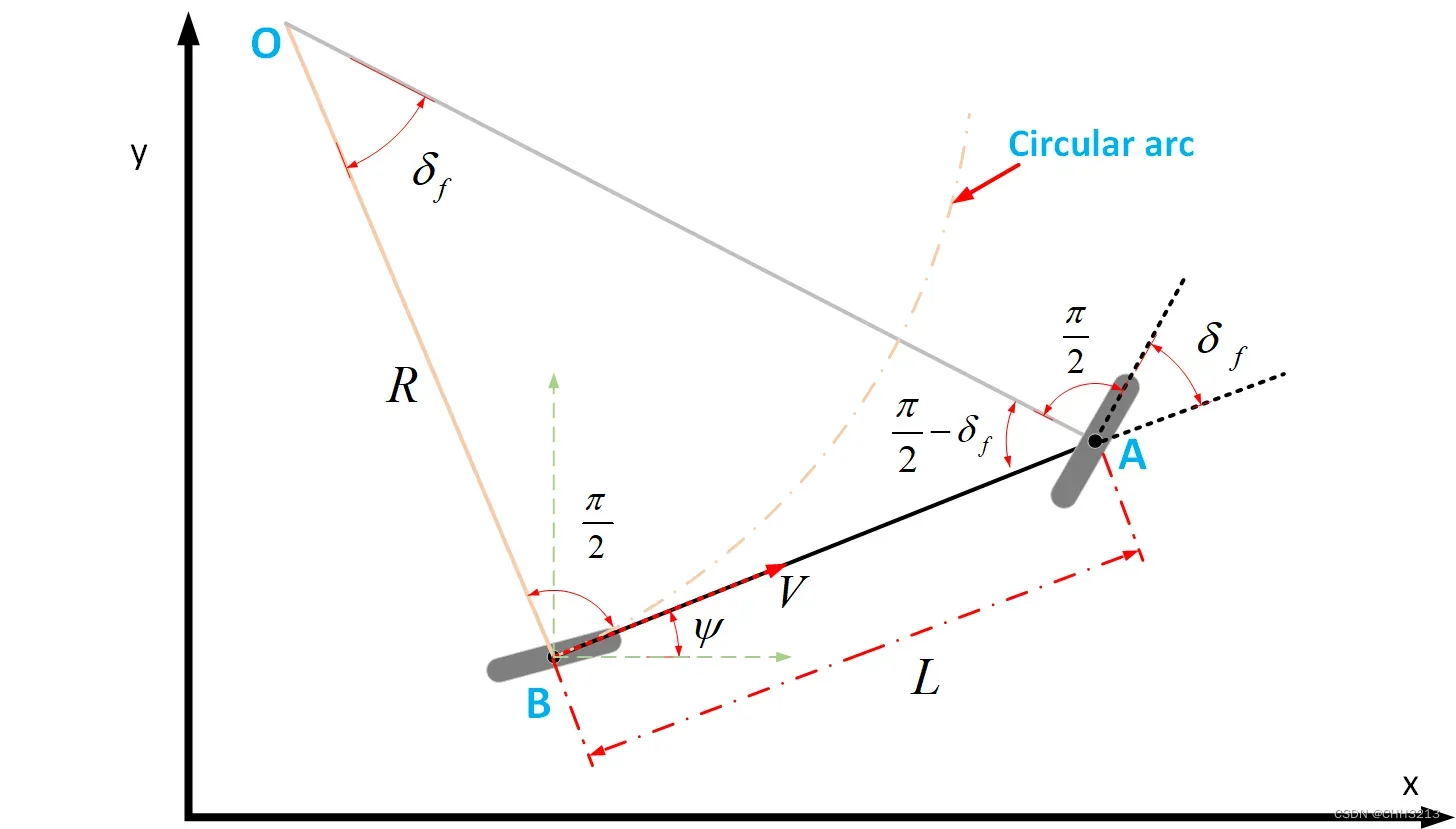
之前讲解了车辆的运动学模型，这边以以后轴中心为车辆中心的单车运动学模型为例进行线性化。

以后轴中心为车辆中心的单车运动学模型如下：

选取状态量为 ，控制量为 ，则对于参考轨迹的任意一个参考点，用 表示，上式可以改写为:

其中 。对上式在参考点采用泰勒级数展开，并忽略高阶项：

对 和 求雅克比矩阵，有：

则状态量误差的变化量 表示为 :

上式表明状态误差量可以构成线性状态空间。

2. 线性模型离散化

对等式(6)进行前向欧拉离散化，得到

整理后，得到：

式中，为采样步长，为单位矩阵，维度与矩阵一致。

3. python实现

import math
import numpy as np

class KinematicModel_3:
  """假设控制量为转向角delta_f和加速度a
  """

  def __init__(self, x, y, psi, v, L, dt):
    self.x = x
    self.y = y
    self.psi = psi
    self.v = v
    self.L = L
    # 实现是离散的模型
    self.dt = dt

  def update_state(self, a, delta_f):
    self.x = self.x+self.v*math.cos(self.psi)*self.dt
    self.y = self.y+self.v*math.sin(self.psi)*self.dt
    self.psi = self.psi+self.v/self.L*math.tan(delta_f)*self.dt
    self.v = self.v+a*self.dt

  def get_state(self):
    return self.x, self.y, self.psi, self.v

  def state_space(self, ref_delta, ref_yaw):
    """将模型离散化后的状态空间表达

    Args:
        delta (_type_): 参考输入

    Returns:
        _type_: _description_
    """
    A = np.matrix([
      [1.0,0.0,-self.v*self.dt*math.sin(ref_yaw)],
      [0.0, 1.0, self.v*self.dt*math.cos(ref_yaw)],
      [0.0,0.0,1.0]])
    
    B = np.matrix([
        [self.dt*math.cos(ref_yaw), 0],
        [self.dt*math.sin(ref_yaw), 0],
      [self.dt*math.tan(ref_delta), self.v*self.dt/(self.L*math.cos(ref_delta)*math.cos(ref_delta))]
                  ])
    return A,B