0.摘要
深度高斯过程 (DGP) 是高斯过程的层次概括,它将经过良好校准的不确定性估计与多层模型的高度灵活性相结合。 这些模型的最大挑战之一是精确推断是难以处理的。 当前最先进的推理方法变分推理 (VI) 对后验分布采用高斯近似。 这可能是一般多峰后验的潜在较差的单峰近似。 在这项工作中,我们为后验的非高斯性质提供了证据,并且我们应用随机梯度哈密顿蒙特卡罗方法来生成样本。 为了有效地优化超参数,我们引入了移动窗口 MCEM 算法。 与 VI 对应物相比,这会以更低的计算成本产生明显更好的预测。 因此,我们的方法为 DGP 中的推理建立了新的最新技术。
1.介绍
深度高斯过程 (DGP) [Damianou and Lawrence, 2013] 是高度灵活的多层预测模型,可以准确地模拟不确定性。 特别是,它们已被证明在从小型(500 个数据点)到大型数据集(500,000 个数据点)的众多监督回归任务中表现良好 [Salimbeni 和 Deisenroth,2017,Bui 等,2016,Cutajar 等 ., 2016]。 与神经网络相比,它们的主要优势在于它们能够捕捉预测中的不确定性。 这使它们成为预测不确定性起关键作用的任务的理想候选者,例如黑盒贝叶斯优化问题和各种安全关键应用,如自动驾驶汽车和医疗诊断。
深度高斯过程为高斯过程 (GP) [Williams and Rasmussen, 1996] 引入了多层层次结构。 GP 是一种非参数模型,它假设任何有限输入集的联合高斯分布。 任何一对输入的协方差由协方差函数确定。 由于非参数和可分析计算,GPs 可能是一个稳健的选择,但是,一个问题是选择协方差函数通常需要手动调整和数据集的专家知识,如果没有手头问题的先验知识,这是不可能的。 在多层层次结构中,隐藏层通过拉伸和扭曲输入空间来克服这一限制,从而产生贝叶斯“自调整”协方差函数,无需任何人工输入即可拟合数据 [Damianou, 2015]。
GP 的深度层次化泛化是以完全连接的前馈方式完成的。 前一层的输出用作下一层的输入。 然而,与神经网络的一个显着区别是层输出是概率而不是精确值,因此不确定性通过网络传播。 图 1 的左侧部分说明了具有单个隐藏层的概念。 隐藏层的输入是输入数据 x,隐藏层 f1 的输出作为输出层的输入数据,输出层本身是由 GPs 形成的。
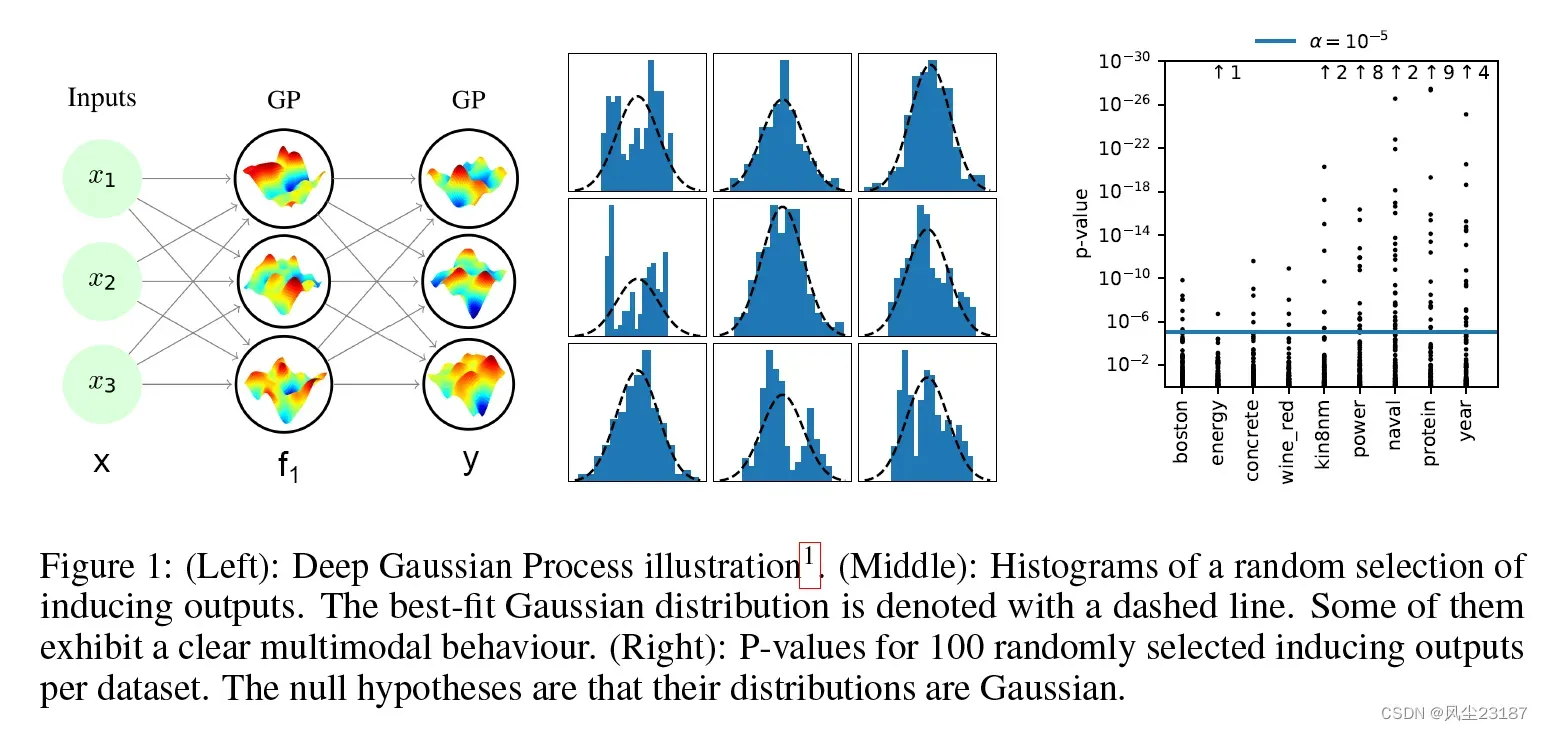
图 1:(左):深度高斯过程插图 1。 (中):随机选择诱导输出的直方图。 最佳拟合高斯分布用虚线表示。 其中一些表现出明显的多模式行为。 (右):每个数据集 100 个随机选择的诱导输出的 P 值。 零假设是它们的分布是高斯分布。
由于使用逆协方差矩阵的计算成本很高,因此在大型数据集的 GP 中进行精确推断是不可行的。 相反,使用一小组伪数据点 (100) 来近似后验,也称为诱导点 [Snelson and Ghahramani, 2006, Titsias, 2009, Quinonero-Candela and Rasmussen, 2005]。 我们在整篇论文中都假设这个诱导点框架。 使用诱导点进行预测以避免计算整个数据集的协方差矩阵。 在 GP 和 DGP 中,诱导输出都被视为需要边缘化的潜在变量。
DGP 中当前最先进的推理方法是双重随机变化推理 (DSVI) [Salimbeni 和 Deisenroth,2017],它已被证明优于期望传播 [Minka,2001,Bui 等人,2016],并且它 也比采用概率反向传播的贝叶斯神经网络 [Hern´andez-Lobato 和 Adams, 2015] 和采用早期推理方法的贝叶斯神经网络(如变异推理 [Graves, 2011]、随机梯度朗之万动力学 [Welling and Teh, 2011)和混合蒙特卡洛 [Neal, 1993]具有更好的性能。 然而,DSVI 的一个缺点是它用高斯近似后验分布。 我们非常自信地表明,对于我们在这项工作中检查的每个数据集,后验分布都是非高斯分布的。 这一发现促使使用具有更灵活后验近似的推理方法
在这项工作中,我们应用了一种新的 DGP 推理方法,即随机梯度哈密顿蒙特卡罗 (SGHMC),这是一种准确有效地捕获后验分布的采样方法。 为了将基于采样的推理方法应用于 DGP,我们必须解决优化大量超参数的问题。 为了解决这个问题,我们提出了移动窗口蒙特卡罗期望最大化,这是一种获得超参数的最大似然 (ML) 估计的新方法。 该方法快速、高效且普遍适用于任何概率模型和 MCMC 采样器。
人们可能期望像 SGHMC 这样的采样方法比 DSVI 这样的变分方法在计算上更加密集。 然而,在 DGP 中,从后验采样成本很低,因为它不需要重新计算逆协方差矩阵,这仅取决于超参数。 此外,计算分层方差在 VI 设置中的成本更高。
最后,我们对各种监督回归和分类任务进行了实验。 我们凭经验表明,我们的工作以较低的计算成本显着改善了对中大型数据集的预测。
我们的贡献可以概括为三点。
- 证明后验的非高斯性。 我们提供的证据表明,我们在这项工作中检查的每个回归数据集都有一个非高斯后验。
- 我们使用 SGHMC 直接从 DGP 的后验分布中采样。 实验表明,这种新的推理方法优于以前的工作。
- 我们介绍了移动窗口 MCEM,这是一种在使用 MCMC 采样器进行推理时有效优化超参数的新算法。
2.背景及相关工作
本节提供回归的高斯过程和深度高斯过程的背景,并建立本文中使用的符号。
2.1 单层GP
高斯过程由后验分布定义
输入
输出
在高斯过程模型下,假定是联合高斯且协方差函数为
,其中,
。
条件分布由似然函数
求得,常用:
精确推理的计算成本是 ,这使得它对于大型数据集在计算上是不可行的。 一种常见的方法是使用一组伪数据点
[Snelson and Ghahramani, 2006, Titsias, 2009] 并将联合概率密度函数写为
给定诱导输出 的
的分布可以表示为
,其中
为了获得 的后验,
必须被边缘化,产生方程
请注意,在给定 的情况下,
有条件地独立于
。
对于单层GPs,VI能够用于边际,VI使用变分后验去近似联合后验分布
,其中
。
的这种选择允许精确推断边际
其中:
需要优化变分参数和 S。 这是通过最小化真实后验和近似后验的 Kullback-Leibler 散度来完成的,这相当于最大化边缘似然的下界(证据下界或 ELBO)
2.2 深层GP
在深度为 的
中,每一层都是一个
,它对函数
建模,其中输入
和输出
对于
如图 1 左侧所示。层的感应输入由
表示,与之相关的感应输出
。
联合概率密度函数可以写成类似于 GP 模型的情况:
2.3 推理(暂略)
推理的目标是边缘化诱导输出 和层输出
并逼近边际似然
。 本节讨论有关推理的先前工作。
双随机变分推理
DSVI 是对 DGP 的变分推理的扩展 [Salimbeni 和 Deisenroth,2017],它用独立的多元高斯 逼近诱导输出
的后验。层输出自然遵循方程式1中的单层模型。
然后通过小批量对层输出进行采样来估计生成的 ELBO 中的第一项,以允许扩展到大型数据集。
高斯过程的基于采样的推理
在相关工作中,Hensman 等人。 [2015] 在单层 GP 中使用混合 MC 采样。 他们考虑了 GP 超参数和诱导输出的联合采样。 由于对 GP 超参数进行采样的成本很高,因此这项工作不能直接扩展到 DGP。 此外,它使用昂贵的方法贝叶斯优化来调整采样器的参数,这进一步限制了其对 DGP 的适用性。
3 深度高斯过程后验分析
4 深度高斯过程的基于采样的推理
5 解耦的深度高斯过程
6实验
我们在 9 个 UCI benchmark 数据集上进行了实验2,范围从小(500 个数据点)到大(500,000 个),以便与基线进行公平比较。 在每个回归任务中,我们测量了平均测试对数似然 (MLL) 并比较了结果。 图 4 显示了 MLL 值及其超过 10 次重复的标准偏差。
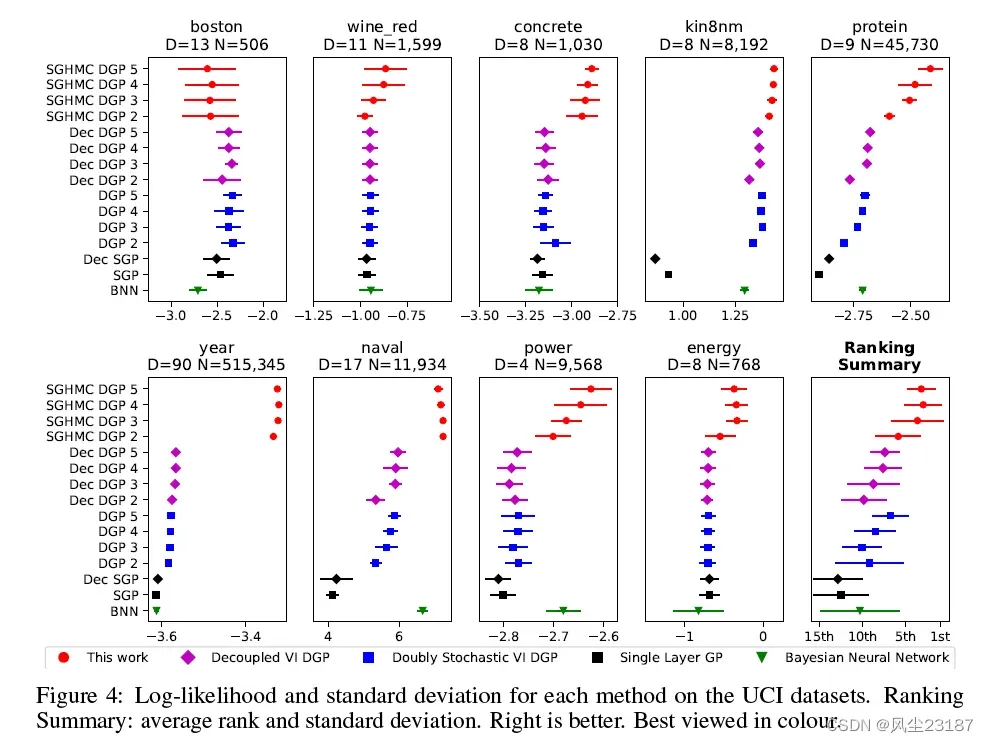
基线:我们实验的主要基线是双重随机 DGP。 为了进行公平的比较,我们使用了与原始论文中相同的参数。 就诱导点的数量而言(诱导输入总是在潜在维度上共享),我们测试了两种变体。 首先,原始的耦合版本,每层 M = 100 个诱导点 (DGP)。 其次,解耦版本 (Dec DGP),平均值为 Ma = 300,方差为 Mb = 50。选择这些数字是为了使单次迭代的运行时间与耦合版本相同。 进一步的基线由耦合(SGP:M = 100)和解耦(Dec SGP:Ma = 300,Mb = 50)单层 GP 提供。 最终基线是具有三个隐藏层和每层 50 个节点的稳健贝叶斯神经网络 (BNN) [Springenberg 等人,2016 年]。
SGHMC DGP(这项工作):该模型的架构与基线模型相同。 M = 100 个诱导输入用于与基线保持一致。 老化阶段包括 20,000 次迭代,随后是采样阶段,在此期间,在 10,000 次迭代过程中抽取了 200 个样本。
MNIST 分类 : SGHMC 在分类问题上也很有效。 使用 Robust-Max [Hern´andez-Lobato et al., 2011] 似然函数,我们将模型应用于 MNIST 数据集。 SGP 和 Dec SGP 模型分别达到了 96.8 % 和 97.7 % 的准确率。 关于深度模型,表现最好的模型是 12 月 DGP 3,达到 98.1%,其次是 SGHMC DGP 3,达到 98.0%,DGP 3 达到 97.8%。 [Salimbeni and Deisenroth, 2017] 报告 DGP 3 的值略高,为 98.11%。这种差异可归因于参数的不同初始化。
哈佛清洁能源项目: 该回归数据集是为哈佛清洁能源项目制作的 [Hachmann et al., 2011]。 它测量有机光伏分子的效率。 它是一个高维数据集(60,000 个数据点和 512 个二进制特征),已知可以从深度模型中受益。 SGHMC DGP 5 建立了新的最先进的预测性能,测试 MLL 为 -0.83。 DGP 2-5 达到 -1:25。 该数据集上的其他可用结果是具有期望传播的 DGPs的-0.99 和 BNN 的 -1.37 [Bui et al., 2016]。
运行时间: 为了支持我们的说法,即 SGHMC 的计算成本低于 DSVI,我们在蛋白质数据集的训练过程中绘制了不同阶段的测试 MLL(图 3 中的右图)。 与 DSVI 相比,SGHMC 收敛速度更快且限制更高。 SGHMC 以 1:6 倍的速度达到了 20,000 次迭代的目标。
7 结论
本文描述并展示了一种新的 DGP 推理方法 SGHMC,该方法从通常的诱导点框架中的后验分布中采样。 我们描述了一种新颖的移动窗口 MCEM 算法,该算法能够以快速有效的方式优化超参数。 这以降低的计算成本显着提高了中大型数据集的性能,从而为 DGP 中的推理建立了新的最新技术。
文章出处登录后可见!
