系列文章目录
深刻易懂地理解:卷积、卷积在图像处理中的应用、从全连接到卷积(一)
深刻易懂地理解:卷积、卷积在图像处理中的应用、从全连接到卷积(二)
三、从全连接到卷积
1.为什么到卷积
MLP是指多层感知机,是全连接网络(前馈神经网络、BP神经网络)的前生,将MLP的激活函数改成其他的函数并且层层相连就形成了全连接网络。
神经网络最开始的模型是感知模型,实质是对各个输入值的先行组合,比如出行有人更关心日期,而另一些人更关心天气,那么其对不同输入的关心程度不一样,这就是早期模型的直观解释。神经单元相互组合,那么其输入和输出有相同的形式,因此可以层层相加,为了避免退化,之间加入非线性函数,这样前馈网络(mlp)就产生了,但问题来了,将很小的图像作为输入,简单叠加几层参数就爆炸了(算力大幅提升后的现在,mlp又重新成为热点),于是节省参数的想法自然出现了,通过共享参数,将一层的神经单元通过滑动的方式处理大得多的输入,这就是一维卷积,显然输入向量被当作同质的东西被处理了,二维卷积于此类似。
通俗的讲MLP这种网络处理图像数据会带来参数量过多的问题,所以才提出了卷积神经网络,利用卷积核去处理完整的特征图,降低了参数量。
2.转化过程
CNN的两个原则:
- 平移不变性(translation invariance):不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”。
- 局部性(locality):神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是“局部性”原则。最终,可以聚合这些局部特征,以在整个图像级别进行预测。
2.1卷积层推导
首先,多层感知机的输入是二维图像,其隐藏表示
在数学上是一个矩阵,在代码中表示为二维张量。其中
和
具有相同的形状。为了方便理解,我们可以认为,无论是输入还是隐藏表示都拥有空间结构。
使用和
分别表示输入图像和隐藏表示中位置
处的像素。为了使每个隐藏神经元都能接收到每个输入像素的信息,我们将参数从权重矩阵(如同我们先前在多层感知机中所做的那样)替换为四阶权重张量W。假设
包含偏置参数,我们可以将全连接层形式化地表示为:
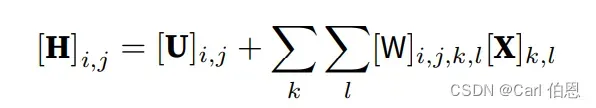
索引 和
通过在正偏移和负偏移之间移动覆盖了整个图像。对于隐藏表示中任意给定位置
处的像素值
,可以通过在
中以
为中心对像素进行加权求和得到,加权使用的权重为
。
现在引用第一个原则:平移不变性。这意味着检测对象在输入 中的平移,应该仅导致隐藏表示H中的平移。也就是说,
和
实际上不依赖于
的值,即
。并且
是⼀个常数,比如u。因此,我们可以简化
定义为:
这就是卷积(convolution)。我们是在使用系数对位置
附近的像素
进行加权得到
。
注意,的系数比
少很多,因为前者不再依赖于图像中的位置。这就是显著的进步!
现在引用第二个原则:局部性。如上所述,为了收集用来训练参数的相关信息,我们不应偏离到距
很远的地方。这意味着在
或
的范围之外,我们可以设置
。因此,我们可以将
重写为:
这就是一个卷积层了,而卷积神经网络是包含卷积层的一类特殊的神经网络。在深度学习研究社区中,V被称为卷积核(convolution kernel)或者滤波器(filter),亦或简单地称之为该卷积层的权重,通常该权重是可学习的参数。当图像处理的局部区域很小时,卷积神经网络与多层感知机的训练差异可能是巨大的:以前,多层感知机可能需要数十亿个参数来表示网络中的一层,而现在卷积神经网络通常只需要几百个参数,而且不需要改变输入或隐藏表示的维数。
定义多个通道的卷积层为:
为输入通道数,其中隐藏表示
中的索引
表示输出通道,而随后的输出
将作为输入进入下⼀个卷积层。
可观看沐神讲解:
19 卷积层【动手学深度学习v2】
2.2图示
用
和
分别表示输入和输出通道的数目,并让
和
为卷积核的高度和宽度。为了获得多个通道的输出,我们可以为每个输出通道创建一个形状为
的卷积核张量,这样卷积核的形状是
。在互相关运算中,每个输出通道先获取所有输入通道,再以对应该输出通道的卷积核计算出结果。
图解: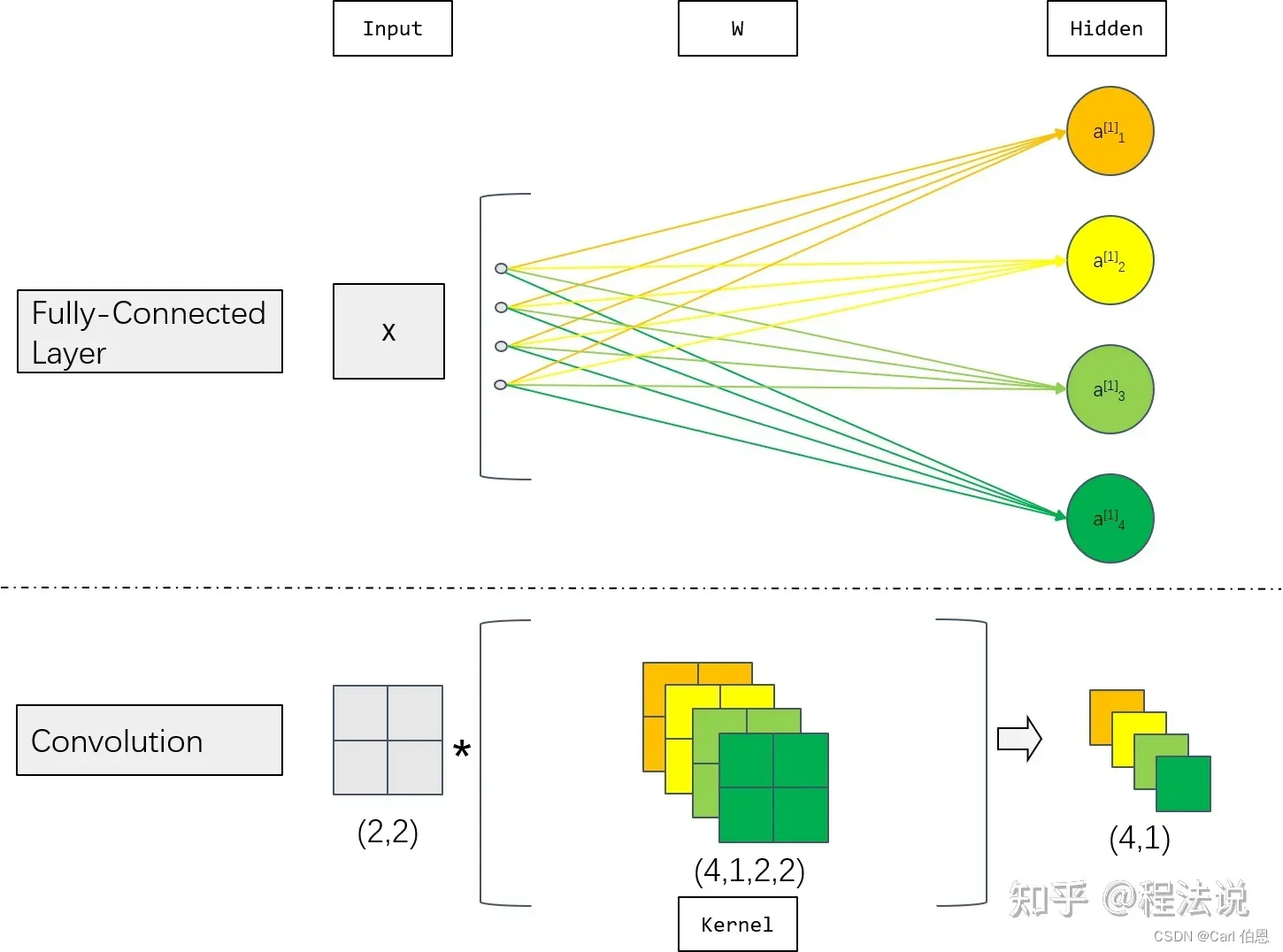
2.3卷积
在数学中,卷积被定义为:
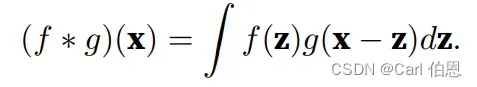
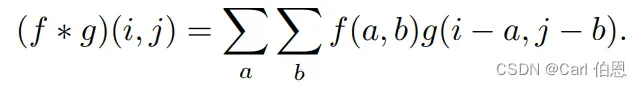
总结
分享一个CNN过程可视化的网页:
Learn Convolutional Neural Network (CNN) in your browser!
文章出处登录后可见!
