原文标题 ：Understanding AutoEncoders with an Example: A Step-by-Step Tutorial

通过示例了解自动编码器：分步教程

第二部分：变分自动编码器

Introduction

自编码器很酷，变分自编码器更酷！

这是“通过示例了解自动编码器”系列的第二篇（也是最后一篇）文章。在第一篇文章中，我们生成了一个合成数据集并构建了一个普通自动编码器来重建圆圈图像。[0]

我们将再次使用相同的合成数据集，因此如果需要，请查看“类似 MNIST 的圆形数据集”部分以进行复习。[0]

在本文中，我们将关注另一种自动编码器：变分自动编码器 (VAE)。我们还将了解著名的重新参数化技巧是什么，以及 Kullback-Leibler 散度/损失的作用。

邀请您在使用 Google Colab 运行随附的 notebook 时阅读本系列文章，这些文章可在我的 GitHub 的“Accompanying Notebooks”存储库中找到：[0]

此外，我建立了一个目录来帮助您浏览两篇文章的主题，如果您将其用作迷你课程并一次通过一个主题来处理内容。

Table of Contents

第一部分：香草自动编码器

• 类似 MNIST 的圆数据集[0]
• The Encoder[0]
• Latent Space[0]
• The Decoder[0]
• Loss Function[0]
• AutoEncoder (AE)[0]
• 奖励：自动编码器作为异常检测器[0]

第二部分：变分自动编码器（本文）

• Variational AutoEncoder (VAE)[0]
• Reparametrization Trick[0]
• Kullback-Leibler 背离/损失[0]
• 损失的规模[0]
• 卷积变分自动编码器 (CVAE)[0]

Variational AutoEncoder (VAE)

在传统的自动编码器中，潜在空间是不连续的，也就是说，不仅在“边缘”之外，而且在训练集中图像映射的点之间都有“空”的潜在空间。这并不是说从“空”空间中的点重建的图像只会产生噪声/垃圾——我们甚至在第一篇文章中得到了一些圆圈——但这并不能保证更复杂的问题。

“那我们可以让潜空间连续吗？”

完全正确！让我们修改 vanilla 自动编码器，使其不在潜在空间中产生点，而是在潜在空间中产生分布。我向您介绍变分自动编码器 (VAE)！

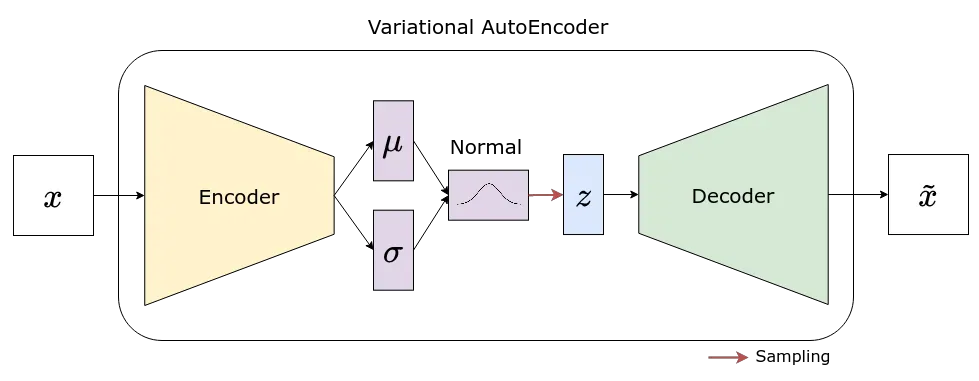
在 VAE 中，编码器不再输出潜在空间，而是生成均值和标准差，每个维度都有一个（与您为向量 z 选择的大小一样多）。然后使用每对均值和标准差来定义相应的分布（我们使用的是正态分布），我们从中采样以获得向量 z 的值。

砰！潜在空间现在是连续的！

另外，还记得我们在第一部分的“编码器”部分将编码器的输出层 (lin_latent) 与模型的其余部分分开吗？现在你可以明白为什么了——在 VAE 中，我们使用基础模型的输出来提供两个输出层：lin_mu 和 lin_var。[0]

EncoderVar(
  (base_model): Sequential(
    (0): Flatten(start_dim=1, end_dim=-1)
    (1): Linear(in_features=784, out_features=2048, bias=True)
    (2): LeakyReLU(negative_slope=0.01)
    (3): Linear(in_features=2048, out_features=2048, bias=True)
    (4): LeakyReLU(negative_slope=0.01)
  )
  (lin_mu): Linear(in_features=2048, out_features=1, bias=True)
  (lin_var): Linear(in_features=2048, out_features=1, bias=True)
)

看起来不错，对吧？但是，有一个小问题……不能通过计算图中的“随机节点”进行反向传播！

上图中的“随机节点”是我们的向量 z，因为它位于表示采样的红色箭头的接收端。

“这是什么意思？”

这意味着，每当在前向传播中引入来自分布的采样时，在该点之前使用的任何参数/权重都无法到达反向传播过程，因此在我们的案例中无法训练编码器。

这看起来很糟糕，我知道，但幸运的是，使用一个小技巧很容易解决它……

Reparametrization Trick

所以，问题是“随机节点”，对吧？如果我们从计算图中消除随机性会怎样？如果随机性来自输入怎么办？它甚至不必是用户提供的输入 – 从字面上看，它可能是一些内部随机输入！

所以，事情是这样的：

• 编码器像以前一样继续产生成对的均值和标准差（两个向量的大小与 z 相同）；
• 在编码器的前向传播中，我们从标准的 Normal(mu=0, std=1) 分布中抽取样本来构建一个与 z 大小相同的随机向量 (epsilon)——这是内部随机输入；

def forward(self, x):
    base_out = self.base_model(x)
        
    self.mu = self.lin_mu(base_out)
    self.log_var = self.lin_var(base_out)
    std = torch.exp(self.log_var/2)
                
    eps = torch.randn_like(self.mu)
    z = self.mu + eps * stdreturn z

• 我们将随机 (eps) 和标准差 (std) 向量相乘，并将平均 (mu) 向量添加到结果中——瞧，我们得到了全新的向量 z！

您可能想知道编码器实际产生了什么，因为标准偏差 (std) 不是编码器的直接输出……

编码器的输出实际上是对数方差 (log_var)，但我们可以使用以下表达式计算标准差 (std)：

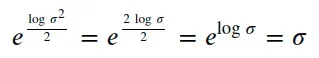
“好吧，我明白了，但那为什么不直接求标准差呢？”

好吧，我们不能有标准差的负值，对吧？但是线性输出层（lin_var）会在各处输出值，负值和正值。理论上，我们可以使用 ReLU 激活函数来只保留正值，当然，但这更像是一种变通方法而不是解决方案。

如果我们将编码器的输出当作方差的对数（而不是方差本身），我们将有效地消除方差的所有负值（这些负值的取幂总是会导致(0, 1] 范围内的值)，而且更好的是，我们做得很顺利，而不是作为截止。此外，由于每次在公式中弹出对数时都很典型，它提高了数值稳定性： -)

清除这些后，让我们检查一下图表现在的样子：

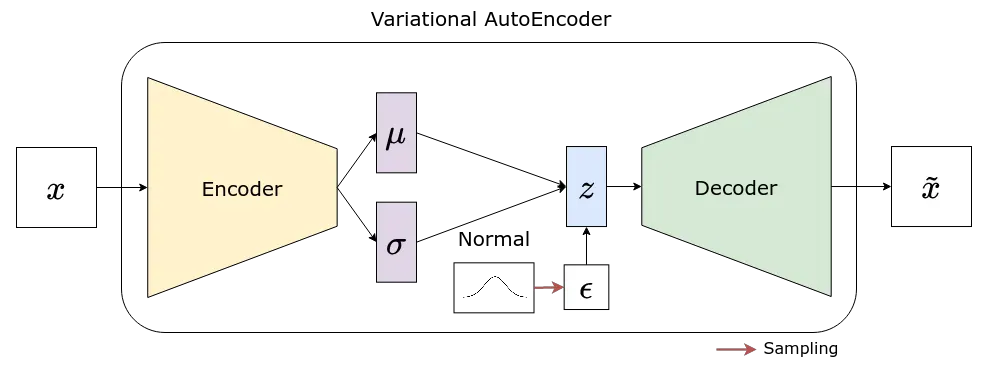
“随机节点”不再存在，因为红色箭头（采样）指向输入（epsilon）。计算图再次完整——因此允许我们模型中的每个参数，从解码器返回到编码器，在反向传播期间更新。简而言之，这就是重新参数化技巧！

在 PyTorch 中，常规采样和使用重新参数化技巧的采样之间的区别在于用于从正态分布采样的方法：sample vs rsample。[0][1][2]

def sample(self, sample_shape=torch.Size()):
    shape = self._extended_shape(sample_shape)
    with torch.no_grad():
        return torch.normal(self.loc.expand(shape),
                            self.scale.expand(shape))def rsample(self, sample_shape=torch.Size()):
    shape = self._extended_shape(sample_shape)
    eps = _standard_normal(shape, 
                           dtype=self.loc.dtype,
                           device=self.loc.device)
    return self.loc + eps * self.scale

rsample 方法执行的操作与我们上面的前向传递完全相同。我们本可以使用 rsample 而不是自己编写代码，但出于教育目的，我认为最好在前向传递本身中明确显示此计算。

“而已？真的？”

真的 – 它不必很复杂 – 这个想法非常简单和优雅。

“那么，我们可以对代码进行这些更改并训练我们的 VAE 了吗？”

没那么快，我们仍然需要讨论另一个损失，即 Kullback-Leibler 散度/损失（简称 KL Loss）。

Kullback-Leibler 背离/损失

KL 散度/损失是衡量两个分布之间差异的指标，q(z) 是我们试图实现的分布，而 p(z) 是我们实际拥有的分布。我们不在这里讨论细节和公式，但我们仍然需要知道，p(z) 越接近 q(z)，散度/损失越低。

“好的，但这如何适用于我们的 VAE？”

分布 p(z) 是我们使用编码器产生的一对均值和标准差得到的正态分布，即我们实际拥有的分布。

另一个分布 q(z) 是标准的 Normal(mu=0, std=1) 分布，这是我们试图实现的分布。

KL 散度/损失越接近编码器生成的标准正态（mu=0，std=1）分布越低。

因此，最小化 KL 损失意味着我们的编码器将为我们的潜在空间（向量 z）的每个维度生成尽可能接近标准正态（mu=0，std=1）的分布。

由于两个分布 p(z) 和 q(z) 都是正态分布，而后者是标准正态分布，KL 散度/损失由下面相对简单的表达式给出：

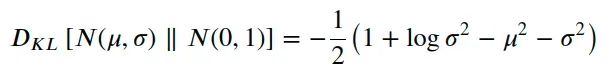
或者，如果您更喜欢在代码中使用它：

def kl_div(mu, std):
    kl_div = -0.5 * (1 + np.log(std**2) - mu**2 - std**2)
    return kl_div

下图说明了两个分布的 KL 散度/损失如何变化，橙色的 p(z)（根据相应的行和列具有不同的属性）和蓝色的 q(z)（标准正态分布）：

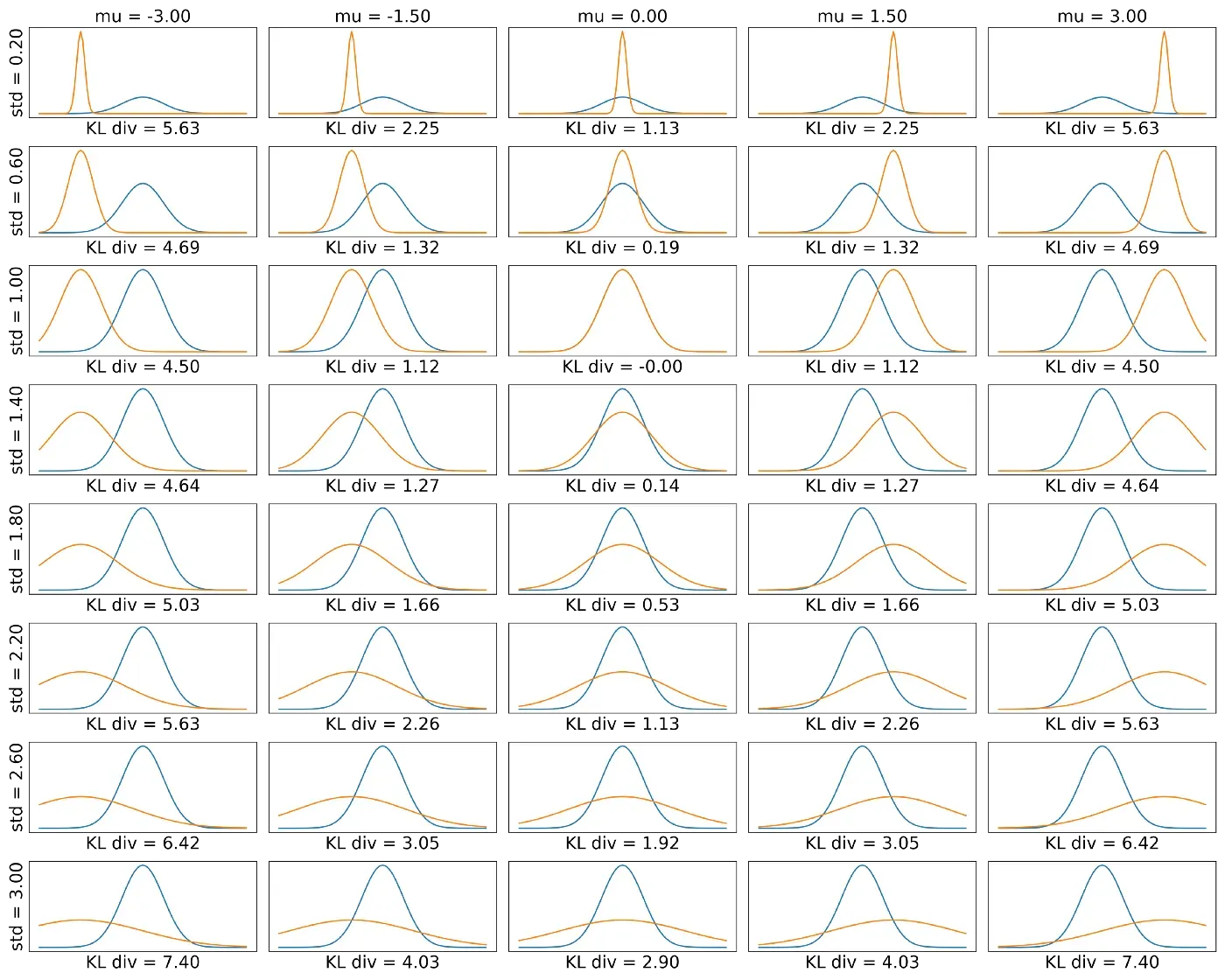
这是相同的数据，这次是热图，以实现更简洁的可视化：

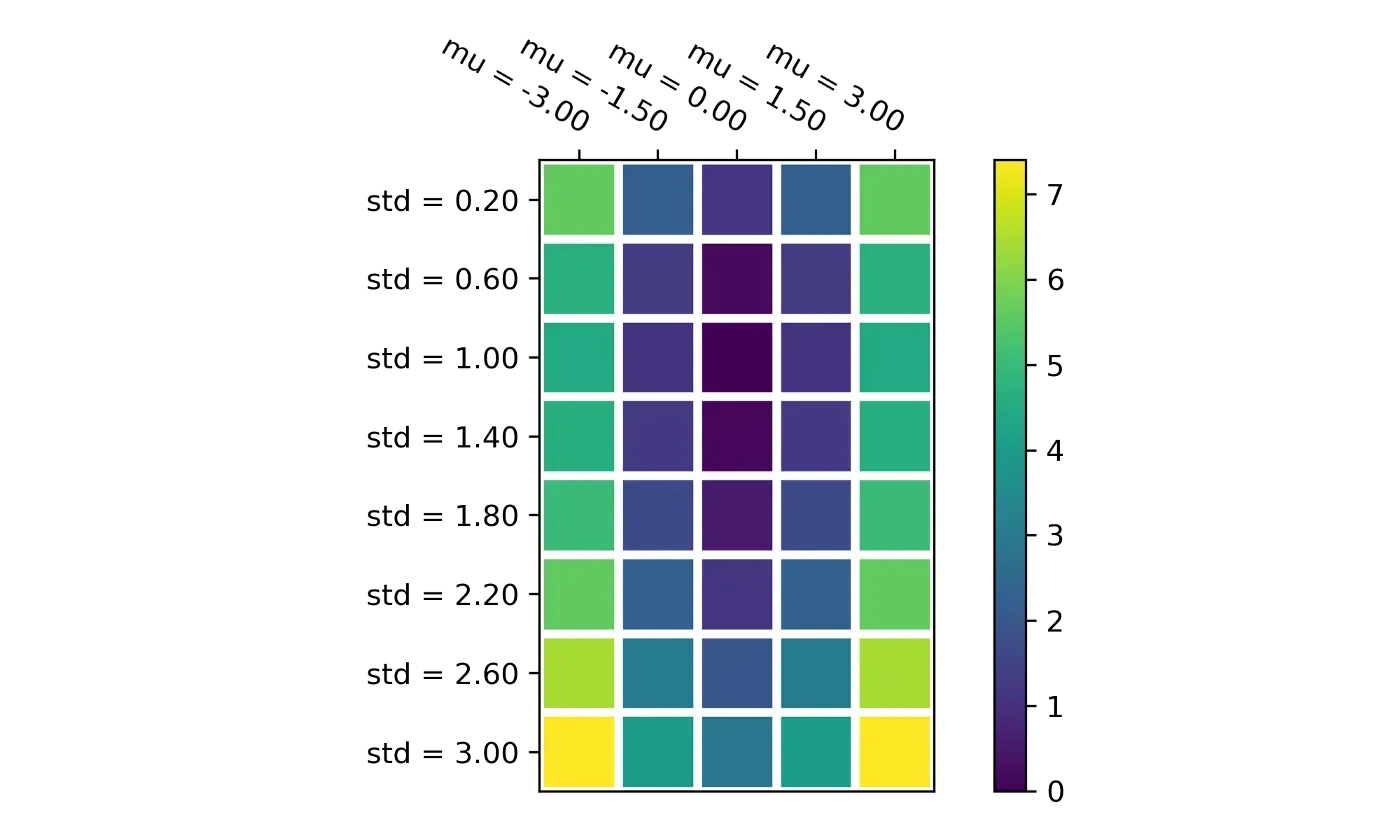
“我们为什么要关心这个，我的意思是，为什么将潜在空间的维度作为标准法线分布很重要？”

因为这将使我们以后的生活更轻松——我们将能够使用众所周知且熟悉的分布（标准正态分布）从潜在空间中进行采样。此外，对于潜在空间的每个维度，训练集中的图像都将映射到标准法线的典型区间（-3.0 到 3.0）。这意味着如果我们的样本也在那个区间内，我们很可能会得到很好的重建。

现在，我们终于可以更改编码器的代码了，变分风格！我们需要修改 forward() 方法（如“重新参数化技巧”部分中所述）并添加一个 kl_loss() 方法来使用我们的编码器产生的均值和对数方差计算 KL 散度/损失：

解码器和自动编码器模型与第一部分的普通自动编码器中的模型保持一致：

“所以，我们将 KL 损失添加到 MSE（或 BCE）损失中，我们可以训练它吗？”

是的，但我们仍然需要考虑…

损失的规模

忽略这个问题很容易——我们已经习惯于在 PyTorch 的损失函数（如 MSE 或 BCE）中使用默认的“均值”作为归约参数，以至于我们甚至可能不会再考虑它。因此，如果我们在处理 KL 损失时简单地默认使用相同的程序，这应该不足为奇，对吧？

嗯，是的，但这可能不适用于培训 VAE。这就是为什么你会看到，在大多数关于 VAE 的教程中，使用“sum”而不是“mean”来减少损失，尽管在大多数情况下，对它背后的原因只字未提。那么让我们仔细看看吧！

我们将从获取一批圆形图像开始，然后对它们进行编码，并使用我们的（未经训练的）模型重建它们。

x, y = next(iter(circles_dl))
zs = encoder_var(x)
reconstructed = decoder_var(zs)

接下来，我们将使用 reduction=’none’ 获得 MSE 损失的原始值：

loss_fn_raw = nn.MSELoss(reduction=’none’)
raw_mse = loss_fn_raw(reconstructed, x)
raw_mse.shape
Output:
torch.Size([32, 1, 28, 28])

不出所料，批次中每个图像 (32) 的每个通道 (1) 的每个像素 (28×28) 都有一个平方误差，总共 25,088 个值。如果我们在损失函数中使用标准缩减（“mean”或“sum”），它们将简单地计算所有 25,088 个值的相应缩减，例如：

raw_mse.sum(), nn.MSELoss(reduction=’sum’)(reconstructed, x)
Output:
(tensor(23960.8066, grad_fn=<SumBackward0>),
 tensor(23960.8066, grad_fn=<MseLossBackward>))

完美的一对！但是我们不必像那样减少它，我们可以更有选择性地计算每个图像的像素的总和，然后才计算这批图像的平均值：

sum_over_pixels = raw_mse.sum(dim=[1, 2, 3])
sum_over_pixels.mean()
Output:
tensor(748.7753, grad_fn=<MeanBackward0>)

看？那是完全不同的结果！我们还可以翻转减少，并首先计算像素的平均值，然后计算批次的总和。下表总结了四种可能的策略：

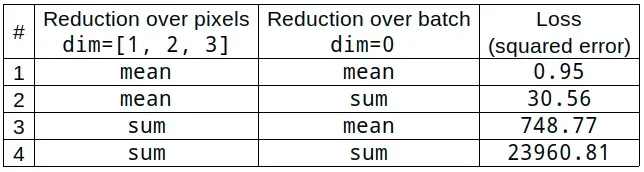
现在，让我们对 KL 损失做同样的事情，使用变分编码器中实现的 kl_loss() 方法获取其原始值：

raw_kl = encoder_var.kl_loss()
raw_kl.shape
Output:
torch.Size([32, 1])

由于 KL 散度/损失是针对潜在空间的每个维度（向量 z）计算的，并且我们选择只有一个维度，因此批次中的每个图像只有一个值。我们选择的缺点是在向量 z (dim=1) 上取“sum”或“mean”总是会产生相同的结果，如下表所示：

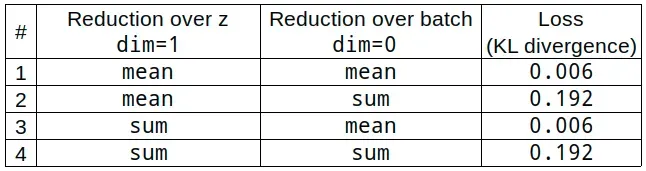
我们将使用组合 #4 来处理 MSE 和 KL 损失，但我鼓励您尝试其他组合并了解它们如何影响模型训练。出于这个原因，我们将在训练循环中手动且显式地减少两次损失：在除第一个之外的每个维度上一次，然后在批次上再次减少。

“如果这些组合都没有产生好的结果怎么办？该怎么办？”

好问题！事实证明，在重建损失中包含一个乘数也是习惯性的。这个因素是您在训练 VAE 时可以调整的超参数。

loss = loss_fn(yhat, x).sum(dim=[1, 2, 3]).sum(dim=0)
kl_loss = model_vae.enc.kl_loss().sum(dim=1).sum(dim=0)
total_loss = reconstruction_loss_factor * loss + kl_loss

如果因子太高，重建损失将主导训练，就好像我们有一个普通的自动编码器。

如果因子太低，KL 损失将主导训练，重建图像不会有任何好处。

Model Training (VAE)

我们需要修改训练循环以考虑损失、重建和 KL，以及前者的乘数。修改属于第二步（第 21 到 29 行，计算损失），并且仅属于第二步。

device = 'cuda' if torch.cuda.is_available() else 'cpu'
model_vae.to(device)
loss_fn = nn.MSELoss(reduction='none')
optim = torch.optim.Adam(model_vae.parameters(), 0.0003)

num_epochs = 30

train_losses = []

reconstruction_loss_factor = 1

for epoch in range(1, num_epochs+1):
    batch_losses = []
    for i, (x, _) in enumerate(circles_dl):
        model_vae.train()
        x = x.to(device)

        # Step 1 - Computes our model's predicted output - forward pass
        yhat = model_vae(x)

        # Step 2 - Computes the loss
        # reduce (sum) over pixels (dim=[1, 2, 3])
        # and then reduce (sum) over batch (dim=0)
        loss = loss_fn(yhat, x).sum(dim=[1, 2, 3]).sum(dim=0)
        # reduce (sum) over z (dim=1)
        # and then reduce (sum) over batch (dim=0)
        kl_loss = model_vae.enc.kl_loss().sum(dim=1).sum(dim=0)
        # we're adding the KL loss to the original MSE loss
        total_loss = reconstruction_loss_factor * loss + kl_loss

        # Step 3 - Computes gradients
        total_loss.backward()
        # Step 4 - Updates parameters using gradients and the learning rate
        optim.step()
        optim.zero_grad()
        
        batch_losses.append(np.array([total_loss.data.item(), 
                                      loss.data.item(), 
                                      kl_loss.data.item()]))

    # Average over batches
    train_losses.append(np.array(batch_losses).mean(axis=0))

    print(f'Epoch {epoch:03d} | Loss >> {train_losses[-1][0]:.4f}/ \
            {train_losses[-1][1]:.4f}/{train_losses[-1][2]:.4f}')

Epoch 001 | Loss >> 4622.8542/4566.6690/56.1851
Epoch 002 | Loss >> 625.7960/554.5768/71.2191
...
Epoch 029 | Loss >> 269.6513/198.1815/71.4698
Epoch 030 | Loss >> 257.9317/182.5780/75.3537

潜在空间分布 (VAE)

如果我们绘制潜在空间 (z) 的直方图（左图），我们会看到，虽然它还不是一个正态分布，但它有点接近它。

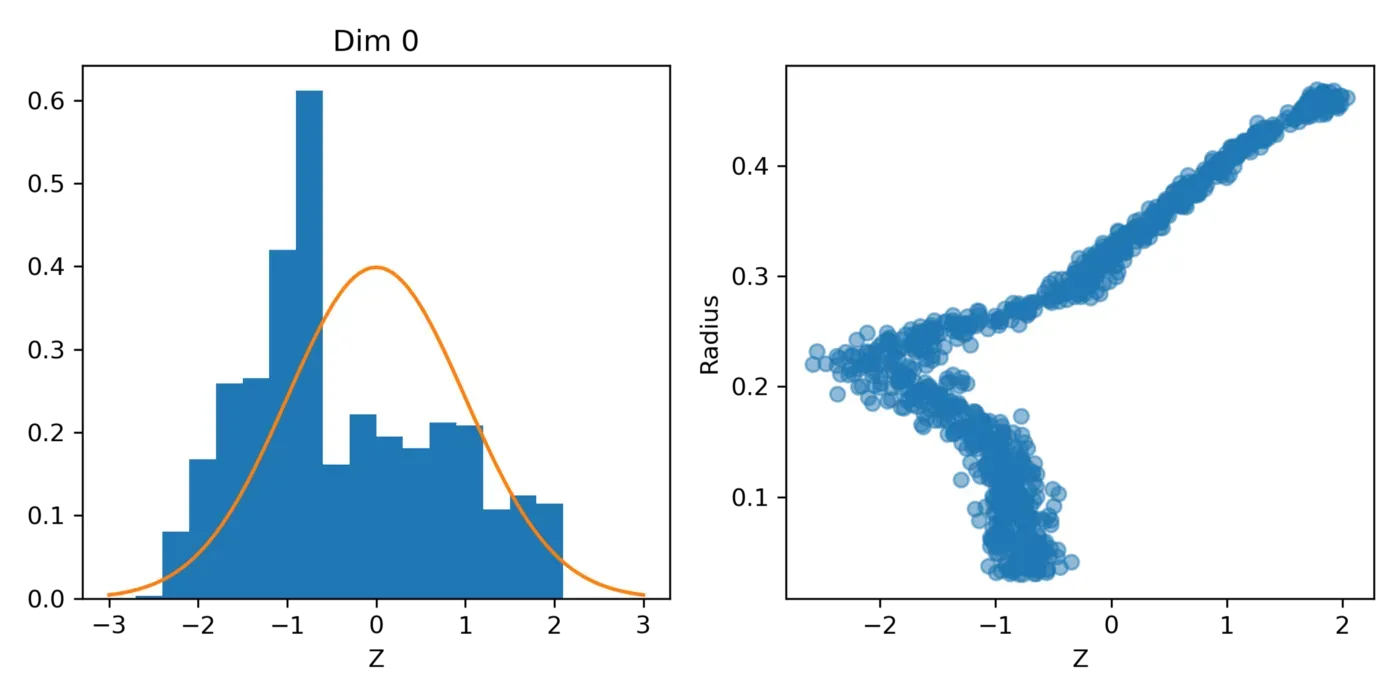
然后，如果我们根据每个圆的相应半径绘制潜在空间，我们将得到右侧的图。在半径的 0.2 标记处仍然有一个“肘部”，但那条垂直线已经消失（来自第一篇文章中训练的普通自动编码器），这意味着我们不应该在重建图像的任何地方看到圆圈的“混合” .让我们来看看！[0]

Reconstruction (VAE)

我们正在重建五个图像，对应于第一篇文章中使用的潜在空间中的相同五个点（-3.0、-0.5、0.0、0.9、3.0）。

别忘了我们的潜在空间现在是连续的！

在标准正态分布的极端（[-3.0] 和 [3.0]）处使用潜在空间中的点生成的图像上仍然存在一些噪声，并且仍然存在一些小半径圆的“混合”（[- 0.5]），但它绝对比普通的自动编码器看起来更好。

现在，是时候进行卷积了！

卷积变分自动编码器 (CVAE)

直到最近，卷积神经网络 (CNN) 还是计算机视觉任务的事实上的标准。尽管 Transformers 现在拥有这个称号，但 CNN 仍然是有用、简单且快速的架构，因此我们将使用它们来构建卷积变分自动编码器 (CVAE)。

我假设您熟悉常规 CNN，以及它们如何用于简单的图像分类任务，因为我们的编码器看起来非常像典型的 CNN：

set_seed(13)

z_size = 1
n_filters = 32
in_channels = 1
img_size = 28
input_shape = (in_channels, img_size, img_size)

base_model = nn.Sequential(
    # in_channels@28x28 -> n_filters@28x28
    nn.Conv2d(in_channels, n_filters, kernel_size=3, stride=1, padding=1),
    nn.LeakyReLU(),
            
    # n_filters@28x28 -> (n_filters*2)@14x14
    nn.Conv2d(n_filters, n_filters*2, kernel_size=3, stride=2, padding=1),
    nn.LeakyReLU(),
    
    # (n_filters*2)@14x14 -> (n_filters*2)@7x7
    nn.Conv2d(n_filters*2, n_filters*2, kernel_size=3, stride=2, padding=1),
    nn.LeakyReLU(),
    
    # (n_filters*2)@7x7 -> (n_filters*2)@7x7
    nn.Conv2d(n_filters*2, n_filters*2, kernel_size=3, stride=1, padding=1),
    nn.LeakyReLU(),
    
    # (n_filters*2)@7x7 -> (n_filters*2)*7*7
    nn.Flatten(),
)

encoder_var_cnn = EncoderVar(input_shape, z_size, base_model)

EncoderVar(
  (base_model): Sequential(
    (0): Conv2d(1, 32, kernel_size=(3, 3), 
                stride=(1, 1), padding=(1, 1))
    (1): LeakyReLU(negative_slope=0.01)
    (2): Conv2d(32, 64, kernel_size=(3, 3), 
                stride=(2, 2), padding=(1, 1))
    (3): LeakyReLU(negative_slope=0.01)
    (4): Conv2d(64, 64, kernel_size=(3, 3), 
                stride=(2, 2), padding=(1, 1))
    (5): LeakyReLU(negative_slope=0.01)
    (6): Conv2d(64, 64, kernel_size=(3, 3),
                stride=(1, 1), padding=(1, 1))
    (7): LeakyReLU(negative_slope=0.01)
    (8): Flatten(start_dim=1, end_dim=-1)
  )
  (lin_mu): Linear(in_features=3136, out_features=1, bias=True)
  (lin_var): Linear(in_features=3136, out_features=1, bias=True)
)

看？编码器的基础模型是 CNN，变分部分由两个线性输出层给出，一个用于均值，另一个用于对数方差，就像我们之前的 VAE 一样。

但是，解码器是完全不同的事情，因为它是使用转置卷积构建的。有关这些“反卷积”的快速概述，请查看我的博客文章：

转置卷积用于将图像从 7×7 像素一直增长到原始大小 28×28：

decoder_cnn = nn.Sequential(
    # z_size -> (n_filters*2)*7*7
    nn.Linear(z_size, (n_filters*2)*int(img_size/4)**2),
    
    # (n_filters*2)*7*7 -> (n_filters*2)@7x7
    nn.Unflatten(1, (n_filters*2, int(img_size/4), int(img_size/4))),
    
    # (n_filters*2)@7x7 -> (n_filters*2)@7x7
    nn.ConvTranspose2d(n_filters*2, n_filters*2, kernel_size=3, stride=1, padding=1, output_padding=0),
    nn.LeakyReLU(),

    # (n_filters*2)@7x7 -> (n_filters*2)@14x14
    nn.ConvTranspose2d(n_filters*2, n_filters*2, kernel_size=3, stride=2, padding=1, output_padding=1),
    nn.LeakyReLU(),
    
    # (n_filters*2)@15x15 -> n_filters@28x28
    nn.ConvTranspose2d(n_filters*2, n_filters, kernel_size=3, stride=2, padding=1, output_padding=1),
    nn.LeakyReLU(),
    
    # n_filters@28x28 -> in_channels@28x28
    nn.ConvTranspose2d(n_filters, in_channels, kernel_size=3, stride=1, padding=1, output_padding=0),
    nn.Sigmoid(),
)

“等等，现在有一个 sigmoid 层？”

接得好！是的，有一个 sigmoid 层，但我们将继续使用 MSE 作为损失函数。

我鼓励您尝试移除 sigmoid 层或将损失函数更改为 BCE，也许还可以调整重建损失因子，然后训练模型以查看其运行情况。

Model Training (CVAE)

尽管我们为编码器和解码器使用了更复杂的架构，但这仍然是一个变分自动编码器，并且训练循环本身与之前完全相同：

device = 'cuda' if torch.cuda.is_available() else 'cpu'
model_vae_cnn = AutoEncoder(encoder_var_cnn, decoder_cnn)
model_vae_cnn.to(device)
loss_fn = nn.MSELoss(reduction='none')
optim = torch.optim.Adam(model_vae_cnn.parameters(), 0.0003)

num_epochs = 30

train_losses = []

reconstruction_loss_factor = 1

for epoch in range(1, num_epochs+1):
    batch_losses = []
    for i, (x, _) in enumerate(circles_dl):
        model_vae_cnn.train()
        x = x.to(device)

        # Step 1 - Computes our model's predicted output - forward pass
        yhat = model_vae_cnn(x)

        # Step 2 - Computes the loss
        loss = loss_fn(yhat, x).sum(dim=[1, 2, 3]).sum(dim=0)
        kl_loss = model_vae_cnn.enc.kl_loss().sum(dim=1).sum(dim=0)
        total_loss = reconstruction_loss_factor * loss + kl_loss

        # Step 3 - Computes gradients
        total_loss.backward()

        # Step 4 - Updates parameters using gradients and the learning rate
        optim.step()
        optim.zero_grad()
        
        batch_losses.append(np.array([total_loss.data.item(), 
                                      loss.data.item(), 
                                      kl_loss.data.item()]))

    # Average over batches
    train_losses.append(np.array(batch_losses).mean(axis=0))

    print(f'Epoch {epoch:03d} | Loss >> {train_losses[-1][0]:.4f}/ \
                  {train_losses[-1][1]:.4f}/{train_losses[-1][2]:.4f}')

Epoch 001 | Loss >> 2188.3729/2118.5622/69.8107
Epoch 002 | Loss >> 615.1194/611.0034/4.1160
...
Epoch 029 | Loss >> 172.8306/85.8559/86.9747
Epoch 030 | Loss >> 169.7600/81.1885/88.5715

潜在空间分布 (CVAE)

如果我们绘制潜在空间 (z) 的直方图（左图），我们会看到，这一次，分布非常接近标准正态分布！

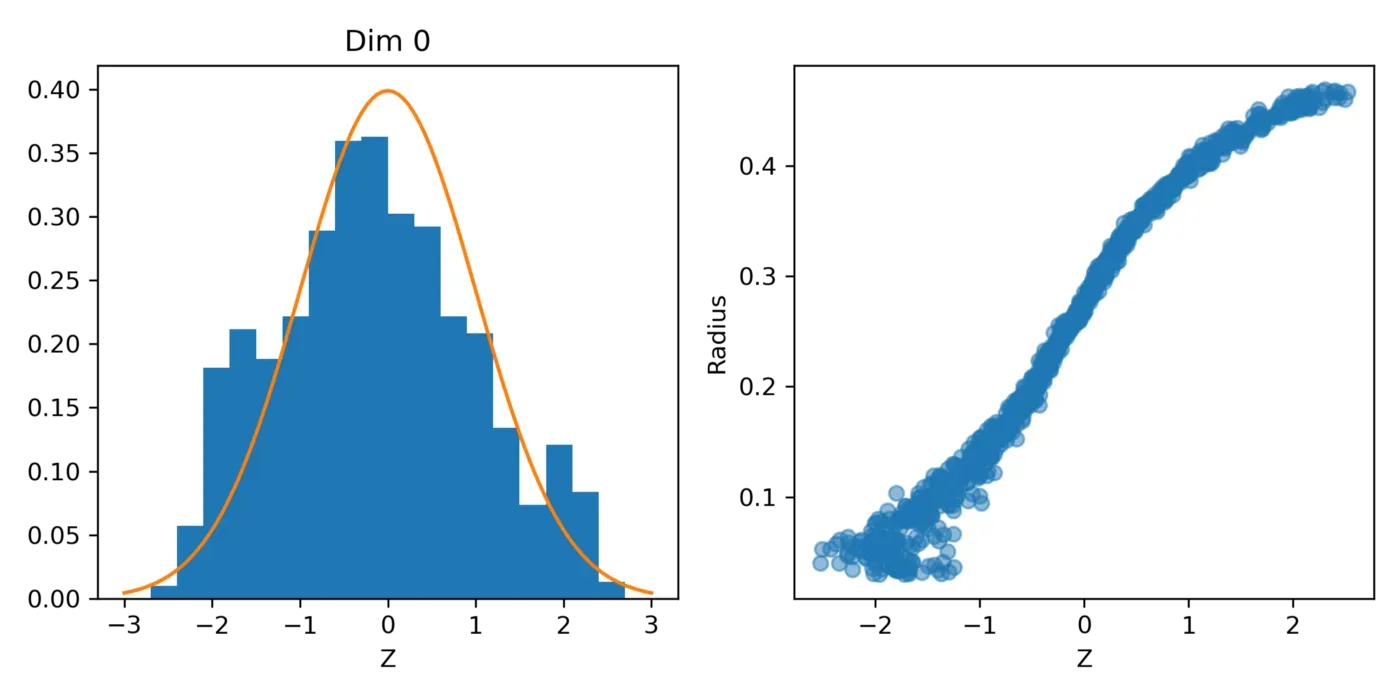
更好的是，如果我们根据每个圆的相应半径绘制潜在空间，则不再有“肘部”——潜在空间和半径两者之间存在大致线性关系。

重建的图像呢？

Reconstruction (CVAE)

如果我们从标准正态分布中对一维潜在空间进行采样，我们将在中心得到平均大小的圆圈，分布最左侧的小圆圈和最右侧的大圆圈分配。这有多棒？

自编码器学会了在潜在空间中表示半径！

我们的工作已经完成:-)

Final Thoughts

感谢您一直坚持到这篇长文的结尾 :-) 但是，尽管这是一篇很长的文章，但这只是一个介绍，它只涵盖了您开始尝试变分自动编码器所需了解的基本工具和技术.

如果您想全面了解自动编码器和生成模型，我推荐 O’Reilly 的 David Foster 的 Generative Deep Learning。

如果您想了解有关 PyTorch、计算机视觉和 NLP 的更多信息，请提供我自己的系列书籍，使用 PyTorch 一步一步进行深度学习，试试看 :-)[0]

如果您有任何想法、意见或问题，请在下方发表评论或通过我的 bio.link 页面联系。[0]

如果您喜欢我的帖子，请考虑通过使用我的推荐页面注册成为 Medium 会员来直接支持我的工作。对于每一个新用户，我都会从 Medium 获得一小笔佣金 :-)[0]