前言
题目： Structural Deep Network Embedding
会议： KDD 2016
论文地址：Structural Deep Network Embedding
这是继node2vec、DeepWalk和LINE后解读的第四篇图嵌入论文。
SDNE和node2vec属于并行研究，二者同时发表在了KDD 2016上。在此之前，除了一些经典的图嵌入或降维算法，如多维标度(MDS)、IsoMap、局部线性嵌入(LLE)和拉普拉斯特征映射，业界主要使用的方法有DeepWalk和LINE。DeepWalk更倾向于具有更高二阶邻近度的节点产生类似的低维表示，LINE则是同时保留了一阶和二阶邻近度。
然而，无论是DeepWalk还是LINE，它们都是浅层模型，很难捕捉高度非线性的网路结构。众所周知，深度神经网络在挖掘非线性特征这一块有着很好的效果，本文也是受此启发，利用自编码器开发了一个结构化的深层网络嵌入模型SDNE。
为了保持局部和全局网络结构，同时也为了让模型对稀疏网络具有鲁棒性，与LINE一样，SDNE也同时考虑了一阶和二阶邻近。本文的很多实验结论与LINE中的完全一致（一个字没变），这也证明了同时考虑一阶和二阶邻近的必要性。
除了LINE采用浅层模型，SDNE采用深层神经网络结构外，SDNE与LINE最大的不同在于如何结合一阶和二阶邻近。在LINE中，为了得到一个既保持了一阶邻近度也保持了二阶邻近度的LINE模型，作者提出了一个办法：分别训练保持一阶邻近度和二阶邻近度的LINE模型，然后将这两种方法训练的嵌入结果连接到每个顶点上。 而在SDNE中，作者直接利用一个损失函数将二者结合起来，然后联合优化。
值得一提的是，LINE的作者（北大）也提到过想要将一阶和二阶邻近联合起来进行优化，但作者只是说希望将其作为未来的研究方向。然后过了一年，也就是2016年，清华大学的研究团队便发表了这篇论文。
除此之外，本文还介绍了precision@k、Mean Average Precision (MAP) 、Micro-F1以及Macro-F1这四个图领域常用的评价指标，这点需要掌握。
理解SDNE需要用到自编码器的知识，因此阅读本文前建议先阅读自编码器(AutoEncoder)。
摘要
现有的网络嵌入方法几乎都采用浅层模型。然而，由于底层网络结构复杂，浅层模型无法捕捉高度非线性的网络结构。因此，如何找到一种能够有效捕获高度非线性网络结构并保持全局和局部结构的方法是一个开放而重要的问题。为了解决这一问题，本文提出了一种结构化深度网络嵌入方法，即SDNE。
具体来说，本文首先提出了一个半监督深度模型，该模型具有多层非线性函数，因此能够捕获高度非线性的网络结构。然后，联合利用一阶和二阶邻近度来保持网络结构：无监督组件使用二阶邻近来捕获全局网络结构，一阶邻近度作为监督分量中的监督信息。通过在半监督深度模型中对它们进行联合优化，SDNE可以保持局部和全局网络结构，并且对稀疏网络具有鲁棒性。
1. 引言
网络嵌入主要面临以下挑战：
- 高度非线性：网络的底层结构是高度非线性的，如何设计一个模型来捕捉高度非线性的结构是相当困难的。
- 结构保持：网络的底层结构非常复杂，顶点的相似性取决于局部和全局网络结构。因此，如何同时保持局部和全局结构是一个难题。
- 稀疏性：许多现实世界的网络通常非常稀疏，仅利用非常有限的观测链路不足以达到令人满意的性能。
现有的许多网络嵌入方法均采用了浅层模型，如IsoMAP、拉普拉斯特征映射(LE)和LINE，但浅层模型的表示能力有限，它们很难捕捉高度非线性的网络结构。尽管有些方法采用了核技术，但核方法也是浅层模型。
在本文提出的模型中，设计了一个由多个非线性函数组成的多层体系结构。多层非线性函数的组合可以将数据映射到高度非线性的表示空间，从而能够捕获高度非线性的网络结构。
同时，为了解决深度模型中的结构保持和稀疏性问题，进一步提出将一阶和二阶邻近度结合到学习过程中。实际上，在LINE中，也提出了将一阶和二阶邻近度结合来保持局部和全局网络结构，同时保持对稀疏网络的鲁棒性。
本文贡献：
- 提出了SDNE，该方法能够将数据映射到高度非线性的潜在空间以保持网络结构，并且对稀疏网络具有鲁棒性。
- 提出了一个新的具有半监督结构的深度模型，该模型同时优化了一阶和二阶邻近。因此，学习到的表示保留了局部和全局网络结构，并且对稀疏网络具有鲁棒性。
- 实验结果证明，SDNE在多标签分类、重建、链接预测和可视化方面具有良好的实用性。
2. 相关工作
2.1 深度神经网络
深度神经网络的最新进展表明，它们具有强大的表示能力，可以为许多类型的数据生成非常有用的表示。但目前的研究工作很少有利用深度模型来学习网络的潜在表示。
2.2 网络嵌入
现有的模型都是浅层模型，无法捕获高度非线性的网络结构。
3. SDNE
3.1 问题定义
；
；
；
和
间如果没有边存在，则
，否则：如果为无权图，
，如果为有权图，
。
一阶邻近度：如果，
和
间存在正的一阶邻近度，否则
和
间一阶邻近度为0。
二阶邻近度：一对节点之间的二阶邻近度描述了这对顶点的邻域结构的接近度。 令表示
与其他节点间的一阶邻近度，那么两个节点间的二阶邻近度就是它们一阶邻近度的相似度量。
本文研究问题定义：给定图，目标是找到每一个节点
的
维向量表示
，这里
，
同时保留了节点间的一阶邻近度和二阶邻近度。
3.2 模型
3.2.1 框架
本文提出了一个半监督深度模型来执行网络嵌入，结果如下所示：
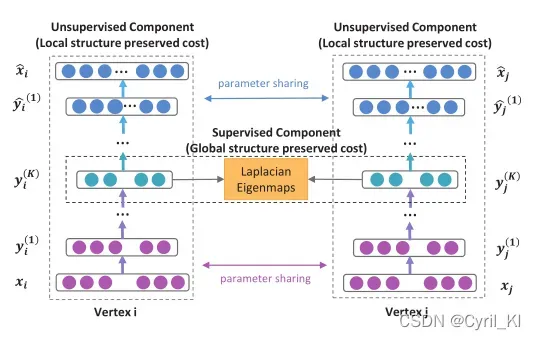
后面再详细解释这个框架。
3.2.2 损失函数
一些术语定义：
下面介绍上述框架怎么来保持二阶邻近度：给定一个图，我们很容易获得它的邻接矩阵
，其中每一个
都是一个向量。
为了来保证二阶邻近度，作者扩展了自编码器。关于自编码器，自编码器(AutoEncoder)中比较详细地介绍，这里简单回顾一下。
自编码器包含两个部分：编码器和解码器，编码器由多个非线性函数组成，这些函数将输入数据映射到表示空间，解码器同样包括多个非线性函数，将表示空间中的表示映射到重构空间。
这时候再来看看上面的框架：
对于一个顶点，首先需要初始化一个
向量，经过一个中间隐层（非线性函数）后，变为
，然后一直变换，直到通过K个隐层后，
将被映射到表示空间，即变为
，然后经过一层层解码，
将被映射到重构空间，即变为
。
变化过程如下：
经过次变换，我们得到了
。然后我们反转编码器的运算过程，就能得到一个与
大小一致的向量
。
自编码器的目标是最小化重建损失，即最小化和
间的不同：
尽管最小化重建损失并不能明确地保持样本之间的相似性，但重建准则可以顺利捕获数据流形，从而保持样本之间的相似性。
回到本文，如果使用作为输入，也就是
，因为每个
表征了顶点
的邻域结构，因此，重构过程将使得具有相似邻域结构的顶点具有相似的潜在表示。 这句话算是SDNE的核心了。
由于网络的稀疏性，邻接矩阵中非零元素的数量远小于零元素的数量，如果直接使用
作为自动编码器的输入，它更容易在
中重建零元素，但这不是我们想要的。为了解决这个问题，作者对非零元素的重构误差施加了比零元素更大的惩罚，修订后的目标函数如下所示：
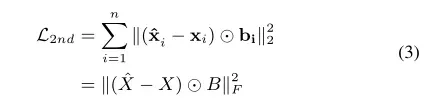
其中表示对应元素相乘，
，如果
，否则
。
也就是说，如果两个顶点间存在链接，会在原有损失的基础上乘上一个大于1的数，这样在最小化损失的时候，就加大了对非零元素的惩罚，这样将不会更容易重建零元素。
(3)式只保证了全局网络结构，还需要通过顶点间的连接情况来保证局部网络结构：
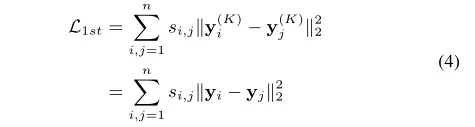
(4)式借鉴了拉普拉斯特征映射的思想：当相似顶点在嵌入空间中映射到很远的地方时，会产生惩罚。
很容易理解，如果两个顶点间存在链接，也就是，那么在损失函数中两个节点（存在链接）的向量表示间的差异将变大，这样我们在最小化差异时会更多地考虑它们间的差异。
因此，(4)式保持了一阶邻近度，即如果两个顶点间存在链接，那么它们会被映射到比较近的位置。
为了同时保持一阶和二阶邻近，将(3)式和(4)式结合起来，损失函数设计如下：
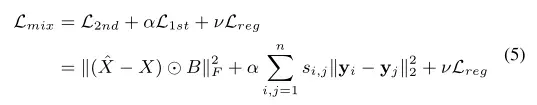
其中是L2正则化项，用来防止过拟合，定义如下：
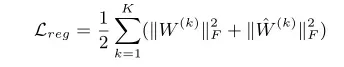
从这里我们就可以看出SDNE和LINE的不同了：LINE是将保持一阶邻近的LINE的嵌入结果和保持二阶邻近的LINE的嵌入结果连接起来，SDNE则是联合优化。
3.2.3 优化
我们的目标是最小化，然后找出自编码器的参数
，即：
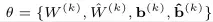
再来看这张图：
和
是编码器的参数，
和
是解码器的参数。因此，我们需要求得
对上述参数的偏导数，其中的关键是对
和
求偏导：
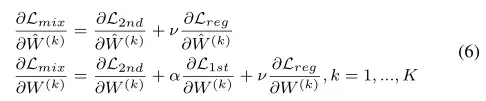
是为了保持一阶邻近，只是需要计算到表示空间，并不需要参与解码运算，因此与
无关。
首先来看：
因为有：
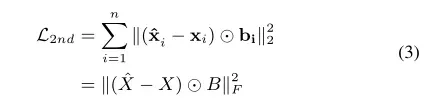
所以有：
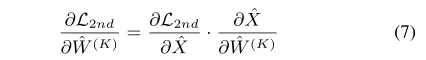
和
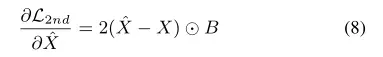
对于(7)中的第二项，因为有：
所以很很容易计算出。
同理，对于，我们可以采用类似的方法来得到
对其的偏导数。
关于：
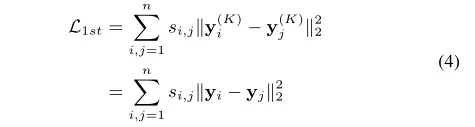
可以重新表述为：
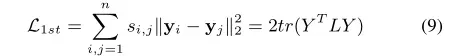
这里，
为度矩阵（对角阵，数值表示节点的度）。
因此，对有：
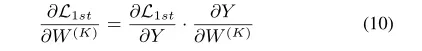
因为有：
因此(10)式中第2项很容易计算。对于第一项，由(9)式我们有：
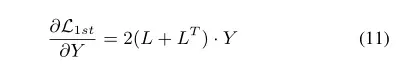
至此，所有偏导数都已经算出，然后再使用SGD进行优化。
值得注意的是，由于模型的高度非线性，因此它在参数空间中存在许多局部最优。为了找到一个好的参数空间区域，作者首先使用深度信念网络(DBN) 对参数进行预训练。
完整的算法可以描述如下：
算法输入：，
的邻接矩阵
，损失函数中的参数
和
；输出：每个节点的嵌入向量表示
和自编码器参数
。
具体步骤：
- 使用深度信念网络得到初始参数
。
- 自编码器输入
。
- 根据
和
和表示空间
，然后损失函数对参数
- 重复3直到收敛。
- 得到表示空间
3.3 分析和讨论
- 新节点：如何学习新到达节点的表示？如果我们已知新节点
与其他所有节点的连接情况，那么我们就能得到
，然后我们将
输入到SDNE中，就能得到其低维向量表示
，这个过程的时间复杂度为
。如果我们不了解连接情况，我们就必须依靠其他信息，比如节点的文本信息，作者表示这一点将作为未来的研究方向。
- 训练复杂度：SDNE的时间复杂度为
，其中
为顶点数，
为网络中节点的平均度，
为隐藏层最大维数，
为迭代次数。参数
与
4. 实验
4.1 数据集
五个网络数据集，包括三个社交网络、一个引文网络和一个语言网络。数据集用于三个实际应用：多标签分类、链接预测和可视化。
数据集介绍如下：
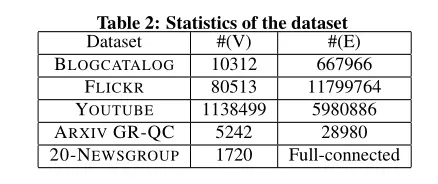
4.2 Baseline
DeepWalk、LINE、GraRep、拉普拉斯特征映射(LE)、Common Neighbor(使用公共邻居的个数来度量顶点间的相似性)。
4.3 评价指标
以前的论文中没有介绍过评价指标，因此这里重点看一下。
本文完成了重建、链接预测、多标签分类和可视化的任务。
（1）对于重建和链路预测，使用precision@k和Mean Average Precision (MAP) 作为评价指标：
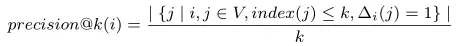precision@k是一个搜索推荐评价指标，index(j)是第j个顶点的排名索引，表示
和
间存在链接。假设查询得到的前K个结果中有n个相关结果，返回n/K。如果结果数不够K，补齐到K（补的都是不相关结果）。
那么对于链接预测，到底怎么计算呢？我们知道在链接预测中，比如我们随机去掉30%的边，那么剩下的70%就是训练集，那30%为测试集。经过图嵌入算法我们可以得到每个节点的低维向量表示，然后我们就可以计算出所有节点间的两两相似度，然后进行排序。 然后需要剔除掉这些节点对中原本存在于训练集中的边，剔除后参与排序的边有两种可能：一是测试集中存在的边，二是原本不存在的边。计算precision@k时，取前k对节点，然后观察里面有几条边属于测试集，然后计算比例即可。
另一个评价指标为MAP：
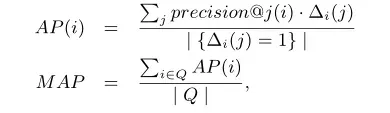
（2）对于多标签分类任务，使用micro-F1和macro-F1作为评价指标。对于二分类问题，可将测试样例根据其真实类别和分类器预测类别划分为：
- True Positive ：预测为正，实际也为正
- False Positive ：预测为正，实际为负
- False Negative ：预测与负、实际为正
- True Negative：预测为负、实际也为负
多分类问题中，对于每一类，我们都可以算出它的F1分数：
其中P为查准率（精确率），R为查全率（召回率）。
而Macro-F1就为所有类别F1分数平均值：
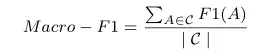
Micro-F1：
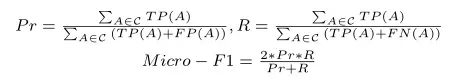
4.4 参数设置
在各个数据上，每层的神经元个数如表3所示：
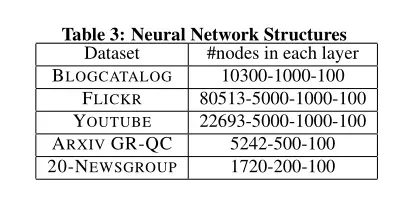
- 对于SDNE，在验证集上使网格搜索法找到初始的
。
- 对于LINE，随机梯度下降的mini-batch的size为1，初始学习率为0.025，负例样本个数为5，样本总数100亿。
- 对于DeepWalk，窗口长度
，路径长度40，每个节点40条路径。
- 对于GraRep，最大矩阵转换步长设置为5。
4.5 实验结果
4.5.1 网络重建
给定一个网络，使用不同的网络嵌入方法来学习网络表示，然后预测原始网络的链接。由于原始网络中的现有链路是已知的，并且可以作为基本事实，因此可以评估不同方法的重建性能，即训练集误差。
各个模型的precision@k和MAP如图3和表4所示：
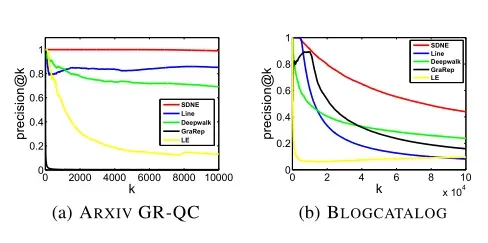
可以看出：
- 图3显示了precision@k当k增加时，SDNE的平均值始终是最高的，这表明SDNE能够很好地保持网络结构。
- 对于ARXIV GR-QC网络，SDNE的precision@k可以达到100%，并保持在100%左右，直到k增加到10000。这表明SDNE几乎可以完美地重建该数据集中的原始网络，特别是考虑到该数据集中的链路总数为28980。
- 虽然SDNE和LINE都利用一阶和二阶邻近性来保持网络结构，但SDNE实现了更好的性能。原因可能有两方面：（1）LINE采用浅层结构，难以捕捉底层网络中的高度非线性的结构。（2）SDNE中是联合优化一阶和二阶邻近，LINE中则是将结果相连，效果可能会差一些。
4.5.2 多标签分类
顶点的表示由网络嵌入方法生成，然后将其用作顶点分类的特征。实验结果如图4和图5所示：
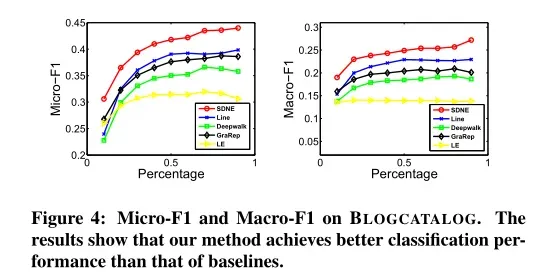
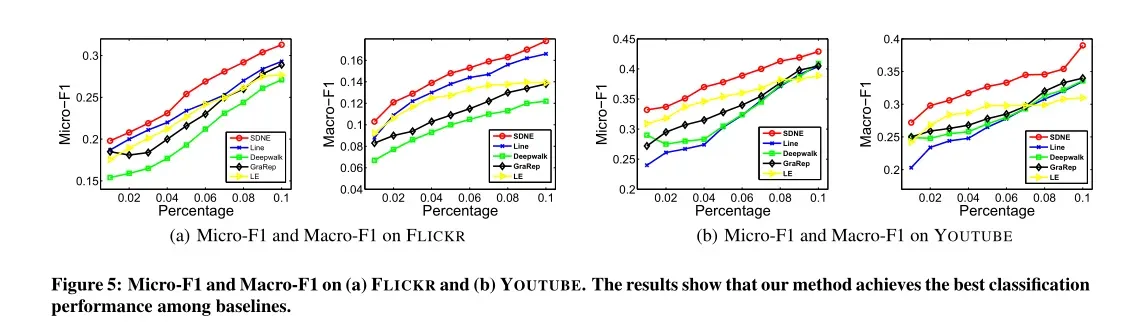
分析如下：
- 无论是在图4还是图5，SDNE的效果都是最好的。这说明SDNE可以很好地被推广到分类任务。
- 在图4(BLOGCATALOG)中，当训练集百分比从60%降低到10%时，SDNE相对于基线的改进幅度更为明显。结果表明，在标记数据有限的情况下，SDNE可以实现比基线更显著的改进。这种优势对于实际应用程序尤其重要，因为标记的数据通常很少。
- 在大多数情况下，DeepWalk的性能都是最差的。原因有两方面：（1）DeepWalk没有明确的目标函数来捕获网络结构。（2）DeepWalk使用随机游走来丰富顶点的邻域，由于其随机性，引入了大量的噪声，特别是对于高度复杂的顶点。
4.5.3 链接预测
与网络重建任务不同，此任务预测未来链接，而不是重建现有链接。因此，该任务可以显示不同网络嵌入方法的可预测性性能。
第一个试验中，随机隐藏15个已有链接（一共约4000个链接）并使用precision@k作为预测隐藏链接的评价指标，结果如表5所示：
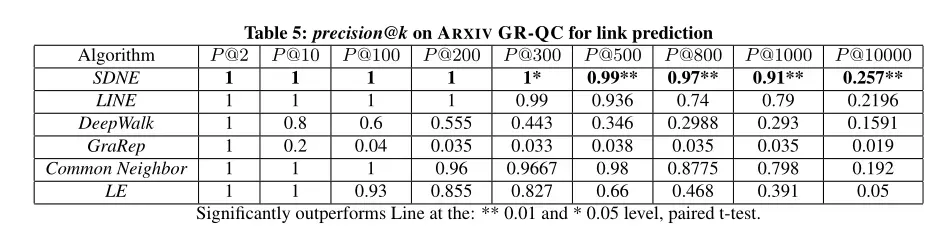
分析如下：
- 当k增加时，SDNE的性能始终优于其他网络嵌入方法。
- 当k=1000时，SDNE精度仍然高于0.9，但其他方法的精度很快下降到0.8以下。这表明，SDNE可以保持高精度的链接排名领先。这种优势对于一些实际应用（如推荐和信息检索）非常重要，因为用户更关心在此类应用中排名靠前的结果。
在第二个实验中，随机移除原始网络中的一部分链路来改变网络的稀疏性，然后重新实验，结果如图6所示：
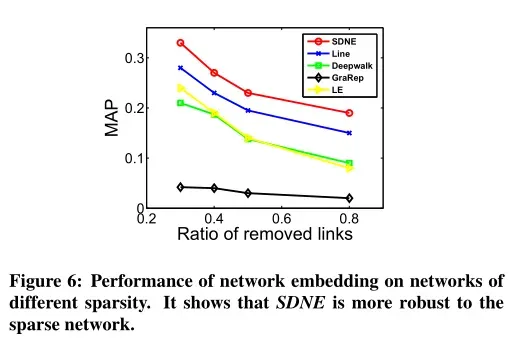
结果表明，SDNE的效果一直都是最好的。当网络较稀疏时，LE与SDNE之间或LE与LINE之间的差距在变大，这说明引入二阶邻近性能够使学习到的表示对稀疏网络更具鲁棒性。
4.5.4 可视化
与LINE中类似，实验结果如下所示：
相同颜色的点应该彼此靠近，因此SDNE的效果无疑是最好的。LE和DeepWalk的结果很差，LINE虽然形成了不同的簇，但在中心部分不同类别间还是有重叠。GraRep结果看起来很好，但每个类别的界限并不十分清楚。
同样，也可以使用KL散度作为衡量指标：
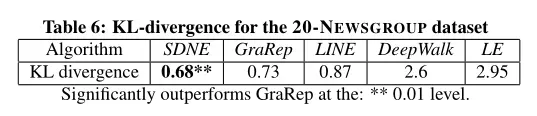
同样可以看出，SDNE的效果是最佳的。
4.6 参数灵敏度
图8(a)展示了嵌入维度对模型性能的影响：
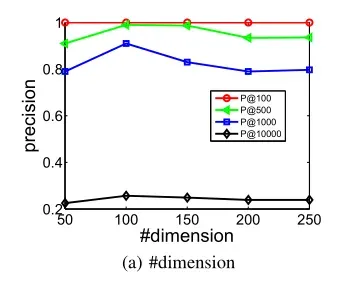
可以看到，最初性能随着嵌入维度增加而提高，因为更多的维度可以编码更多有用的信息。但是，当维度继续增加时，性能开始缓慢下降，原因是尺寸过大可能会产生噪音，从而降低性能。总的来说，确定潜在嵌入空间的维数总是很重要的，但SDNE对这个参数不是很敏感。
参数用于表征一阶邻近和二阶邻近的考虑程度：
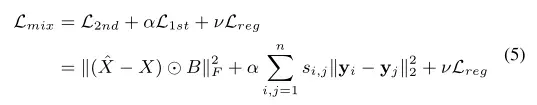实验结果如图8(b)所示：
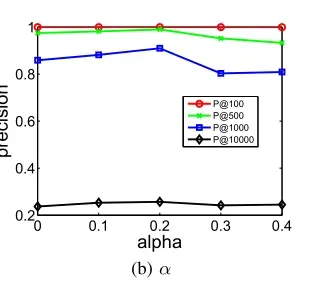
当时，模型表现完全由二阶邻近来决定，当
和
时，性能开始提升。实验结果表明，一阶和二阶邻近性对于网络嵌入方法表征网络结构是必不可少的。
参数用于惩罚零元素，
越大，模型越容易重构非零元素。实验结果如图8©所示：
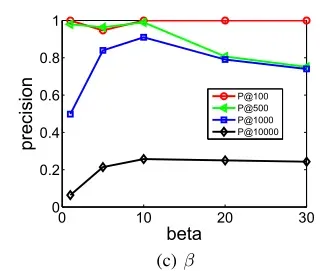
当时，结果并不好，因为在这种情况下，模型将平等地重构训练网络中的非零元素和零元素。当
太大时，性能也会降低，原因是在这种情况下，模型在执行重建时几乎忽略零元素，并且易于保持任何一对节点之间的相似性。然而，许多零元素仍然表示顶点之间的差异，因此性能下降。该实验表明，在进行网络嵌入时，我们应该更多地关注训练网络中非零元素的重构误差，但不能完全忽略零元素的重构误差。
5. 结论
本文提出了一种新的网络嵌入方法SDNE：为了捕获高度非线性的网络结构，设计了一个具有多层非线性函数的半监督深度模型，然后，为了进一步解决结构保持和稀疏性问题，联合利用一阶邻近和二阶邻近来描述局部和全局网络结构。通过在半监督深度模型中对一阶和二阶邻近进行联合优化，学习到的表示保持了局部-全局结构，并且对稀疏网络具有鲁棒性。
版权声明：本文为博主Cyril_KI原创文章，版权归属原作者，如果侵权，请联系我们删除！
原文链接：https://blog.csdn.net/Cyril_KI/article/details/122633318
