前言：

暑假的时候看别人的优秀论文，看到有篇论文使用了牛顿高斯法求函数解析式，就用代码实现了。我还找到了matlab提供的两个命令以及其他可推广的新方法，时隔两个月把这些东西写下来，希望能够帮到有需要的人。

目录

一、待求方程

论文是王毅、李妃、钟叔亮的《饮酒驾车的优化模型》。

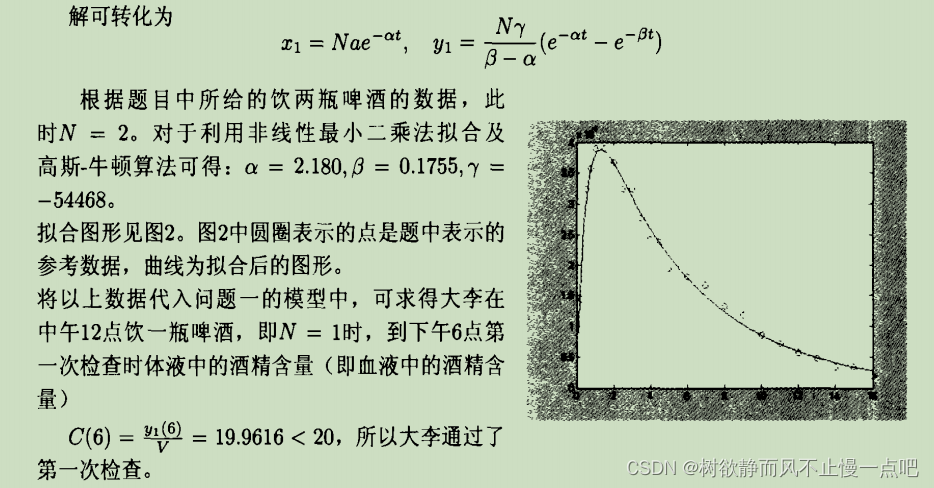
 第一行y（t）为待求方程，也是之后图例和代码中出现的待求参数方程。

t与y的数据来自于2004年全国大学生数学建模竞赛的C题。

二、拟合精度对比（不含文内高斯牛顿代码拟合精度）

论文里gamma值有点大。把gamma放缩后画出的拟合曲线与用fittype命令和lsqnonlin命令拟合参数得到的拟合曲线并原始数据画在一张图上，可以得到：

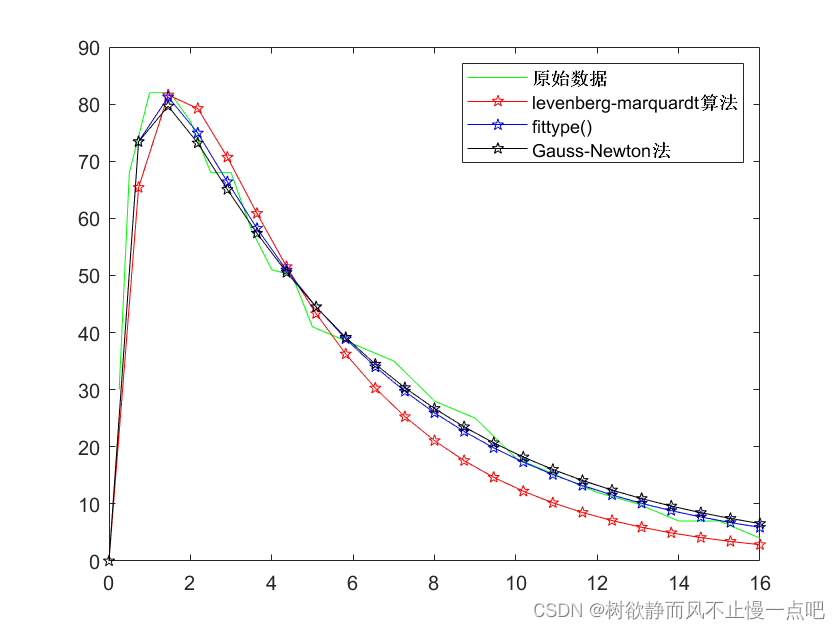
求得拟合精度r^2分别为0.821627940456343，0.768826904267846，0.729379158007370（顺序为右上角图例从上到下）。

 三、介绍两种拟合命令

是lsqnonlin()和fittype()，在matlab文档中已介绍得很好了。

四、高斯牛顿算法代码

基本原理知乎、百度百科上已经介绍得很好了。

[优化] Gauss-Newton非线性最小二乘算法 – 知乎

%% 高斯-牛顿迭代法求非线性最小二乘优化问题
clear
close all
clc

%% 真实数据
N = 2;
x = [0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16];
y_real =[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4];

%% 构造函数f(a,b,c)
syms x_ alpha beta gamma;
arg = [alpha;beta;gamma];
f(alpha,beta,gamma,x_) = N*gamma/(beta-alpha)*(exp(-1*alpha*x_)-exp(-1*beta*x_));

%% 估计初始值
ff = fittype('2*gamma/(beta-alpha)*(exp(-1*alpha*x)-exp(-1*beta*x));','independent','x','coefficients',{'alpha','beta','gamma'});
cfun = fit(x',y_real',ff);
ae = cfun.alpha;
be = cfun.beta;
ce = cfun.gamma;

%% 参数优化收敛条件
itr = 100;    %迭代次数
esp = 1e-10;  %收敛精度
num_itr = 0;  %初始迭代次数
last_cost = 0;%初始收敛精度

%% 高斯牛顿主循环
Jacobi = jacobian(f,arg);
for i=1:itr
    H = 0;
    b = 0;
    cost = 0;
    J = [0 0 0];
    for j = 1:size(x,2)
        error = y_real(j)-f(ae,be,ce,x(j));        
        %用MATLAB库函数求出的雅克比矩阵Jacobian
         J_ = -Jacobi(ae,be,ce,x(j));  %因为y_real(j)-f(ae,be,ce,x(j))，所以要添个负号
         for k=1:3
            J(k) = J_(k);
         end     
        H = H + J'*J;
        b = b+ -J'*error;
        cost = cost + error^2;
    end

    %判断收敛条件是否满足
    if abs((cost-last_cost)/cost)<esp
        break
    end
    num_itr = i;
    last_cost = cost;
    disp(['第',num2str(i),'次迭代后,残差总和为：', num2str(double(cost))])
    %ldlt分解求解dx
    [L,D] = ldl(H);
    bH = sum(b,2);
    dx = L'\(D\(L\bH));
    
    %矩阵直接求逆求解dx
    ae = vpa(ae+dx(1),16); %放低精度，加快运算速度
    be = vpa(be+dx(2),16);
    ce = vpa(ce+dx(3),16);
end

fprintf('总迭代次数为：%d\n',num_itr);
disp(['最优系数alpha = ', num2str(double(ae))])
disp(['最优系数beta = ', num2str(double(be))])
disp(['最优系数gamma = ', num2str(double(ce))])
a = double(ae);
b = double(be);
c = double(ce);
y_pred = N*c/(b-a)*(exp(-1*a*x)-exp(-1*b*x));
R2 = 1-sum((y_pred-y_real).^2)/sum((y_real-mean(y_real)).^2);
disp(['拟合优度R2 = ', num2str(R2)])

figure(1)
scatter(x,y_real,100,'black','.');
hold on;
plot(x,f(ae,be,ce,x),'-','linewidth',1.2);
grid on;
box on;
legend('\bf实测数据','\bf拟合曲线')
xlabel('\itt')
ylabel('\ity')

注：先用fittype估计参数的初值。

使用高斯牛顿法，在收敛精度为10^(-10)条件下求得alpha = 0.1855，beta = 2.0079，gamma = 104.273，拟合精度为0.98569。

这里简单提一下用矩阵求解AX=b的方法（下文内容来自matlab文档）：

通过ldl（）将分块对角矩阵 D 和置换下三角矩阵存储在 L 中，使得 A = L*D*L'。分块对角矩阵 D 在其对角上具有 1×1 和 2×2 个分块。

示例 1 – 双输出形式的 ldl

双输出形式的 ldl 返回 L 和 D，使得 A-(L*D*L') 较小，L 是置换单位下三角矩阵，D 是分块 2×2 对角矩阵。另外还要注意，由于 A 是正定矩阵，D 的对角元素全为正数：

[LA,DA] = ldl(A); 
fprintf(1, ...
'The factorization error ||A - LA*DA*LA''|| is %g\n', ...
norm(A - LA*DA*LA'));
neginds = find(diag(DA) < 0)

给定 a b，使用 LA、DA 对 Ax=b 求解：

bA = sum(A,2);
x = LA'\(DA\(LA\bA));
fprintf(...
'The absolute error norm ||x - ones(size(bA))|| is %g\n', ...
norm(x - ones(size(bA))));

示例 2 – 三输出形式的 ldl

三输出形式也返回置换矩阵，这样 L 实际上就是单位下三角矩阵：

[Lm, Dm, Pm] = ldl(M);
fprintf(1, ...
'The error norm ||Pm''*M*Pm - Lm*Dm*Lm''|| is %g\n', ...
norm(Pm'*M*Pm - Lm*Dm*Lm'));
fprintf(1, ...
'The difference between Lm and tril(Lm) is %g\n', ...
norm(Lm - tril(Lm)));

给定 b，使用 Lm、Dm 和 Pm 对 Mx=b 求解：

bM = sum(M,2);

x = Pm*(Lm'\(Dm\(Lm\(Pm'*bM))));

fprintf(...

'The absolute error norm ||x - ones(size(b))|| is %g\n', ...

norm(x - ones(size(bM))));

可用来反解出[优化] Gauss-Newton非线性最小二乘算法 – 知乎公式[4]的dx。

五、其他可用算法

过后和搞机器学习的同学沟通还发现有个多项式回归法，可以修改参数调节拟合函数的最高次项，需要调参，弹性大，还是挺有意思的。而且用python包只要几行代码，减少写代码工作量。