马上期末考试了，就用这篇博客充当一下复习记录吧。一些部分可能有误，还请各位大佬批评指正。

第 1 章 绪论

• 理解神经网络、深度学习与人工智能的之间的关系；
• 掌握机器学习与深度学习的步骤；

有关神经网络、深度学习与人工智能的关系

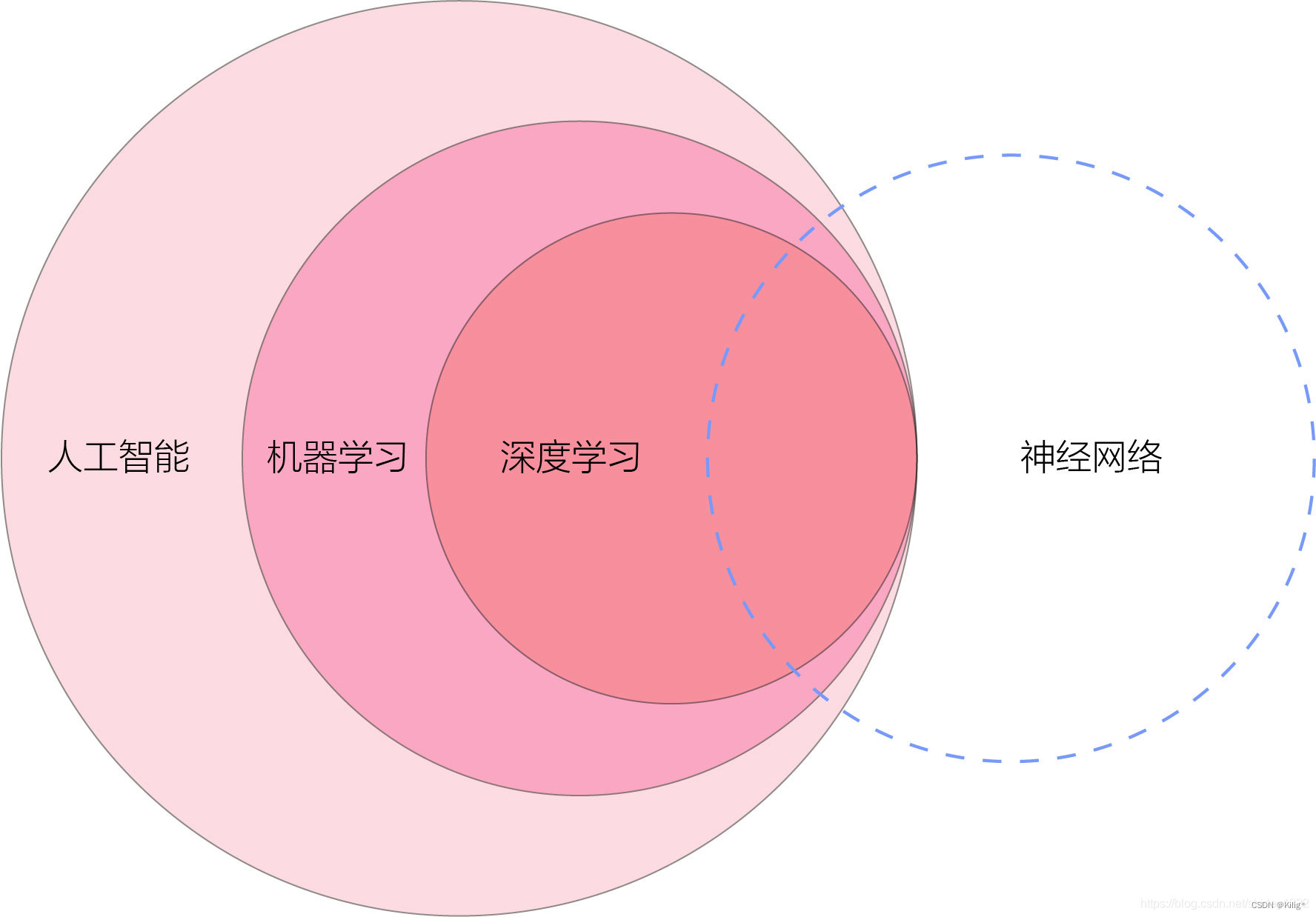
链接: 图片博客来源
理解:深度学习是人工智能的一个子集合，而神经网络和深度学习又有交集。
那么，为什么神经网络和深度学习不是相互包含的关系呢？
神经网络中除了深度学习还有什么？
深度学习中除了神经网络还有什么?
问题:深度学习中除了神经网络还有什么?
深度学习可以采用神经网络模型，也可以采用其他模型（比如深度信念网络是一种概率图模型）. 但是，由于神经网络模型可以比较容易地解决贡献度分配问题，因此神经网络模型成为深度学习中主要采用的模型参考
又或者周志华老师的深度森林，其实也是深度学习但却不是神经网络。

问题:神经网络中除了深度学习还有什么?
个人理解，深度学习是一些比较深的模型。而一些比较简单的神经网络（如单层感知机或者2层神经网络等）这些比较“浅”的模型虽然是神经网络但却不是深度学习。

因此神经网络与深度学习并不是相互包含的关系，深度学习与神经网络彼此有交集却并不等价也不存在包含关系。

问题：机器学习的步骤
首先，什么是机器学习？
机器学习（Machine Learning，ML）是指从有限的观测数据中学习（或“猜测”）出具有一般性的规律，并利用这些规律对未知数据进行预测的方法。
那么机器学习的步骤可以表示如下:

数据预处理:进行如缺失值处理、数据格式统一、数据归一化等操作。

特征提取:根据某些方法提取出有用的特征，提取出有用的特征，去除多余的或者起到干扰作用的特征，又或者在图像分类中提取边缘、在文本分类中去除停用词等。

特征转换:对提取出来的特征进行转换，如降维（PCA或LDA等方法）或升维。使得数据具有更好的表现力。

预测：选定一个合适的模型，学习一个函数（利用优化方法将损失函数降到最小）并在测试集上进行预测。

问题:深度学习的步骤

通过多层的特征转换，把原始数据变成更高层次、更抽象的表示．这些学习到的表示可以替代人工设计的特征，从而避免“特征工程”。数据预处理去哪了？

第 2 章 机器学习概述

• 掌握什么是机器学习；常见的机器学习类型；
• 掌握机器学习四要素；
• 理解机器学习的几个关键点。

问题:什么是机器学习
根据维基百科对机器学习的解释:
机器学习(Machine Learning,ML)是指从有限的观测数据中学习(或“猜测”)出具有一般性的规律，并利用这些规律对未知数据进行预测的方法.

问题:常见的机器学习类型
常见的机器学习有有监督学习、无监督学习、半监督学习、强化学习等。

有监督学习：对每一个样本都有“标准答案”，机器学习根据“标准答案”利用损失函数计算损失，通过对损失函数的最小化达到模型学习的目的。如分类、回归等问题。

无监督学习：每一个样本都没有“标准答案”，利用这些数据解决模式识别中的问题（如类别划分）。常见的无监督学习有PCA、聚类、核密度估计等。

半监督学习：部分样本有“标准答案”部分样本没有。利用这些数据训练一个模型来解决问题（分类、回归等）。

问题:机器学习四要素

• 数据
• 模型：实现任务的数学模型，如决策树、支持向量机，k-means等模型。
• 学习准则：衡量模型的好坏，也是模型的学习目标，如在有监督学习中学习准则即为损失函数，如分类中的交叉熵损失或者回归问题中的MSE损失。
• 优化算法：能够是学习准则的到目标的方法，如梯度下降法等方法。
  以上四点为机器学习的四要素。

理解机器学习的几个关键点
待定

第 3 章 线性模型

• 掌握交叉熵损失
• 掌握MSE 损失

交叉熵和MSE损失的异同:
异：交叉熵是用于分类问题的，而MSE是用于回归问题的。
同：二者都是损失函数，都通过使损失函数最小从而找到最优模型的参数。

交叉熵损失
推导待定
公式:
二分类
在二分类的情况下，模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为 和 ，此时表达式为( 以为底) :

其中:
表示样本 的label，正类为 1 ，负类为 0
表示样本 预测为正类的概率

如何直观理解:
损失函数的作用是什么？
是衡量模型表现好坏的指标，也是模型学习的目标，因此当模型表现较为好时，此时应该有较小的。在上述公式中。
为单个样本的损失，根据上述公式

那么，当样本的真实值为1也就是时，此时那么根据函数，越接近于1，也就是模型认为该样本为正类的概率越大（正确的）此时越小；而若越接近于0，也就是模型认为该样本为负类的概率越大（错误的），此时越大。

当样本的真实值为0也就是时，此时那么根据函数，越接近于1，也就是模型认为该样本为正类的概率越大（错误的）此时越大；而若越接近于0，也就是模型认为该样本为负类的概率越大（正确的），此时越小。
多分类同理
多分类的情况实际上就是对二分类的扩展：

其中:

• —类别的数量
  一符号函数（ 0 或 1 )，如果样本 的真实类别等于 取 1 ，否则取 0
  一观测样本 属于类别 的预测概率

参考:分类模型的 Loss 为什么使用 cross entropy 而不是 classification error 或 squared error

MSE损失
计算预测值和真实值之间的欧式距离。预测值和真实值越接近，两者的均方差就越小
均方差函数常用于线性回归(linear regression)，即函数拟合(function fitting)。
很好理解，使用（）即可衡量第个点真实值与预测值之间的差距。
那么为什么要有平方呢？
这是因为（）可能会出现负值，而加绝对值又不太好处理，因此用平方来表示。
那么为什么要求和之后除以呢？
m为点的个数，除以m相当于取平均，可以反映整体的拟合状况。
那么为什么除以m之后还要除以2呢？
其实除不除都可以，只不过损失函数在误差反向传播或者优化时要进行求导。那么平方项求导之后前方就会有系数2，刚好与分母上的2相消。

第 4 章 前馈神经网络

• 掌握神经网络特征
• 激活函数(常用激活函数:S 型激活函数、斜坡型激活函数、复合激活函数)；
• 掌握前馈神经网络结构
• 掌握前向传播及反向传播算法

神经网络的主要特征:

1. 信息表示是分布式的（非局部的）；
2. 记忆和知识是存储在单元之间的连接上；
3. 通过逐渐改变单元之间的连接强度来学习新的知识。

激活函数
激活函数的几个特征

• 连续并可导（允许少数点上不可导）的非线性函数。
• 激活函数及其导函数要尽可能的简单
• 激活函数的导函数的值域要在一个合适的区间内

常用激活函数:S 型激活函数、斜坡型激活函数、复合激活函数

S 型激活函数
S 型激活函数是指Sigmoid型函数，常用的 Sigmoid型函数有Logistic函数和Tanh函数。

优点：

• Logistic函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。
• 连续函数，便于求导。

缺点：

• sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和现象，意味着函数会变得很平，并且对输入的微小改变会变得不敏感。
• 在反向传播时，当梯度接近于0，权重基本不会更新，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
• sigmoid函数的输出不是0均值的，会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。
• 计算复杂度高，因为sigmoid函数是指数形式。

Tanh函数是 0 均值的，因此实际应用中 Tanh 会比 sigmoid 更好。但是仍然存在梯度饱和与exp计算的问题

• 计算简单，计算速度快。
• 在一定程度上缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度。
• 不会像S型激活函数那样出现饱和现象。

缺点:

• 输出不是0均值的，会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。
• 由于RELU函数在小于0的部分导数始终为0，因此如果参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU 神经元在所有的训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远不能被激活。也就是死亡RELU现象。

Leaky RELU
为了解决函数中的死亡现象，做出了适当改进:不再让小于0的部分恒等于0。
其中 是一个很小的常数。而也可以作为一个参数来学习。Parametric ReLU，PReLU，这样不同的神经元就可以有不同的激活函数，相对更加灵活。
但即使这样仍然有一个问题没有解决，输出并不是0中心化的。因此为了解决这一问题，又提出了

ELU

其中 是一个超参数, 决定 时的饱和曲线,并调整输出均值在 0附近。虽然ELU解决了死亡RELU的问题，也解决了输出的0中心化问题，但是由于引入了e，提高了计算的复杂度，因此运行起来相对会慢一些。

其中𝑃(𝑋 ≤ 𝑥)是高斯分布𝒩(𝜇, 𝜎2)的累积分布函数，其中𝜇, 𝜎为超参数，一般设𝜇 = 0, 𝜎 = 1即可．由于高斯分布的累积分布函数为S型函数，因此GELU函数可以用Tanh函数或Logistic函数来近似.

前馈神经网络结构

• 各神经元分别属于不同的层，层内无连接。
• 相邻两层之间的神经元全部两两连接。
• 整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示。

前向传播及反向传播算法
可以看这位大佬的博文，讲的很清楚。
神经网络BP反向传播算法原理和详细推导流程

第 5 章 卷积神经网络

• 理解什么是卷积神经网络，其三个结构特征；
• 掌握卷积过程和不同类型的卷积（窄卷积、宽卷积和等宽卷积）；
• 掌握卷积神经网络中卷积核、卷积层、卷积网络结构；
• 了解各种不同类型的卷积（空洞卷积等）；
• 理解残差网络机理

卷积神经网络以及其三个结构特征

卷积神经网络（Convolutional Neural Network，CNN或ConvNet）是一种
具有局部连接、权重共享等特性的深层前馈神经网络．

特征:

• 局部连接:在卷积层（假设是第𝑙 层）中的每一个神经元都只和前一层（第𝑙 − 1层）中某个局部窗口内的神经元相连，构成一个局部连接网络
• 权重共享:为一个卷积核只捕捉输入数据中的一种特定的局部特征．因此，如果要提取多种特征就需要使用多个不同的卷积核
• 空间或时间上的次采样

卷积过程和不同类型的卷积
当卷积核在输入图像上扫描时，将卷积核与输入图像中对应位置的数值逐个相乘，最后汇总求和，就得到该位置的卷积结果。不断移动卷积核，就可算出各个位置的卷积结果。

• 窄卷积：步长 𝑇 = 1 ，两端不补零 𝑃 = 0 ，卷积后输出长度为 𝑀 − 𝐾 + 1
• 宽卷积：步长 𝑇 = 1 ，两端补零 𝑃 = 𝐾 − 1 ，卷积后输出长度 𝑀 + 𝐾 − 1
• 等宽卷积：步长 𝑇 = 1 ，两端补零 𝑃 =(𝐾 − 1)/2 ，卷积后输出长度 𝑀
  （M为输入序列长度，K为窗口大小）

掌握卷积神经网络中卷积核、卷积层、卷积网络结构
卷积层
输入：D个特征映射 M × N × D
输出：P个特征映射 M′ × N′ × P

卷积网络是由卷积层、汇聚层、全连接层交叉堆叠而成。

• 趋向于小卷积、大深度
• 趋向于全卷积

各种不同类型的卷积（空洞卷积等）
问题的产生:如何增加输出单元的感受野?
解决方法:

1. 增加卷积核的大小 -缺点:增加参数数量,模型变复杂
2. 增加层数来实现 -缺点: 增加参数数量,模型变复杂
3. 在卷积之前进行汇聚操作 -缺点:汇聚操作会丢失信息

针对以上，提出了空洞卷积:
空洞卷积通过给卷积核插入“空洞”来变相地增加其大小．如果在卷积核的每两个元素之间插入𝐷 − 1个空洞，卷积核的有效大小为𝐾′ = 𝐾 + (𝐾 − 1) × (𝐷 − 1)其中𝐷 称为膨胀率（Dilation Rate）．当𝐷 = 1时卷积核为普通的卷积核．

残差网络机理
残差网络提出的背景。网络越深，表达性能越强。那么网络越深，就一定越优秀吗？

并不是这样的，在网络的训练过程中随着网络层数的增加，网络发生了退化（degradation）的现象：随着网络层数的增多，训练集loss逐渐下降，然后趋于饱和，当你再增加网络深度的话，训练集loss反而会增大。

那么为什么会出现这种现象呢？
在一层又一层的卷积中，是特征的提取过程，但是随着特征的提取也会丢失掉很多信息。在前向传输的过程中，随着层数的加深，特征图包含的图像信息会逐层减少，因此若网络过深可能会起到反作用。

那么如何避免这种情况呢，能不能在提取特征的同时保证信息不丢失？
针对这一问题，残差网络被提了出来。

第 6 章 循环神经网络

• 掌握递归神经网络（RNN）的前向传播，理解反向传播过程(BPTT)；
• 理解梯度消失和梯度爆炸形成原因；
• 掌握 LSTM 结构及核心思想；
• 了解 LSTM 的训练过程（误差反向传播）；
• 了解 LSTM 的变体。

掌握递归神经网络（RNN）的前向传播，理解反向传播过程(BPTT)
前向传播:
其中，表示时刻的输入，表示时刻的隐状态，表示时刻的输出。