VMD如何确定分解层数（一）：最优变分模态分解（OVMD）—VMD分解的基础上确定分解层数和更新步长

上篇博文已经讲述了VMD的分解机制，关于其中的参数，特别是分解层数如何确定的问题，这篇文章给出一个解决方法：最优变分模态分解（OVMD），利用中心频率法确定分解层数K，利用残差指数指标确定更新步长tau。

关于利用中心频率法确定分解层数的文章，无论国内还是国外都有较多的讲述。这里直接上代码。

tic
clc
clear all

load('IMF1_1.mat')
x=IMF1_1;
t=1:length(IMF1_1);

%--------- some sample parameters forVMD：对于VMD样品参数进行设置---------------
alpha = 2000;       % moderate bandwidth constraint：适度的带宽约束/惩罚因子
tau = 0.0244;          % noise-tolerance (no strict fidelity enforcement)：噪声容限（没有严格的保真度执行）
K = 7;              % modes：分解的模态数
DC = 0;             % no DC part imposed：无直流部分
init = 1;           % initialize omegas uniformly  ：omegas的均匀初始化
tol = 1e-7 ;        
%--------------- Run actual VMD code:数据进行vmd分解---------------------------
[u, u_hat, omega] = VMD(x, alpha, tau, K, DC, init, tol);
figure;
imfn=u;
n=size(imfn,1); %size(X,1),返回矩阵X的行数；size(X,2),返回矩阵X的列数；N=size(X,2)，就是把矩阵X的列数赋值给N


for n1=1:n
    subplot(n,1,n1);
    plot(t,u(n1,:));%输出IMF分量，a(:,n)则表示矩阵a的第n列元素，u(n1,:)表示矩阵u的n1行元素
    ylabel(['IMF' ,int2str(n1)],'fontsize',11);%int2str(i)是将数值i四舍五入后转变成字符，y轴命名
end
 xlabel('样本序列','fontsize',14,'fontname','宋体');


%时间\itt/s
 toc;
 %----------------------计算中心频率确定分解个数K-----------------------------
#####################;%求矩阵列的平均值

average即为计算得出的中心频率，因为是要确定分解层数，所以需要我们从K=1开始，不断增加输入，每输入一个K值就进行一次计算。最后输入的K值是几，比如说最后K=5，或者K=11，这个不能确定，要看具体的处理结果。可以确定K值的依据为：一旦出现相似频率，此时的K值被确定为最佳K值。

通过上述代码计算，我们计算出不同k值下的中心频率的结果：

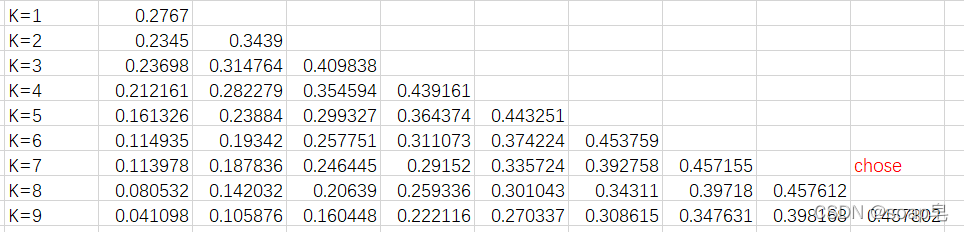
注意看，我们观察各分解情况下，各层分解最后的数值，可以看到，当分解层数为7的时候，中心频率已经稳定下来了，数值为0.457155，当分解层数为8时，中心频率的数值为0.457612，当分解层数为9时，中心频率为0.457802。所以确定分解的层数为7。

确定了VMD的分解层数之后，可以进一步确定另一个参数tau，这里只有确定了分解层数后，才能确定tau的具体数值。具体的方法为残差指数法（REI）。具体可以参考这个文献：ShortTerm Wind Speed Forecast With Low Loss of Information Based on Feature Generation of OSVDhttps://www.webofscience.com/wos/woscc/full-record/WOS:000474609400001

相应具体的公式为：

这里简要解释一下具体的含义，U表示各分解模态数，f表示原始信号，N表示信号的个数。所以这个公式可以简单理解为各分解模态加起来与原始信号相比，求最小，以最接近原始信号。下面直接上代码：

 这个代码实际上，在确定tau的范围后，做一个循环，不断进行VMD分解，以求REI达到最小值。根据文献，tau的范围为0到1，其中步长为0.01。这里再次提醒一下，要先确定分解层数，比如上述代码中的分解层数为7.输入K=7后，进行下面的迭代运算。运算结果如下：

这里在tau中找到那个最小值，即为我们要选取的参数tau的数值。找到最小值的操作，可以在MATLAB中直接找寻，也可以将数值导入到EXCEL中进行寻找。

这里把tau直观化：

这样分解层数K和更新步长tau都找到了，将数值带入到VMD分解中，进行计算就OK了。

如果想进一步详细了解，可阅读上面的那篇文献。