清华大学出品：罚梯度范数提高深度学习模型泛化性

1 引言

如果神经网络结构简单，训练样本量不足，训练后的模型分类精度不高；神经网络结构复杂，训练样本量过大，会导致模型拟合过度。因此，如何训练神经网络以提高模型的泛化能力是人工智能领域的一个非常核心的问题。最近，我读了一篇关于这个问题的文章。本文通过在损失函数中加入正则项梯度范数的约束，改进了深度学习模型的泛化。作者从原理和实验两个方面对本文的方法进行了阐述和验证。 在深度学习的理论分析中，连续性是一个非常重要且常用的数学工具。本文采用损失函数 将神经网络的连续性作为数学推导的起点。为了使读者更容易欣赏作者的优美思想，更顺利地进行数学证明，本文补充了本文未进行的数学证明的细节。

论文链接：https://arxiv.org/abs/2202.03599

2连续

给定一个训练数据集 以分发为准 还有一个神经网络 带参数 损失函数是 当需要限制损失函数中的梯度范数时，有以下损失函数 哪里 代表 规范与 是梯度惩罚系数。一般情况下，在损失函数中引入梯度正则化项，使其具有较小的误差 优化过程中的局部常数。越小越好 常数，损失函数越平滑。平坦损失函数的光滑区域便于优化损失函数的权重参数。从而使经过训练的深度学习模型具有更好的泛化能力。
深度学习中一个非常重要且常见的概念是 连续性给一个空间， 功能, 如果有常数, 对于, 它叫 不断的 如果满足以下条件，其中 代表 常数对于参数空间 如果 他有一个社区 和 是 不断的 据说是本地的 不断的直观地说，“常数”描述了输入变化率的输出上限。一小会儿 参数，给定邻域中的任意两点 他们的产量变化范围很小。
根据微分中值定理，给出了一个极小值点 无论如何, 以下公式适用 哪里, 根据 不平等 什么时候, 相应的 常数接近. 因此，通过减小参数的值，模型可以更平滑地收敛.

3 论文方法

在梯度范数约束下，可以得到损失函数的梯度
在本文中，作者提出 此时，有以下推导过程 为了将结果引入受梯度范数约束的损失函数，有以下公式
可以发现，上述公式涉及 矩阵在深度学习中，计算 参数矩阵会带来较高的计算成本，因此需要使用一些近似方法。作者用泰勒展开了损失函数，其中, 还有, 我们去哪儿, 代表一个小值， 表示一个向量，当引入上述公式时 如果 然后
综上所述，可以通过排序得到
哪里, 打电话 为平衡系数，取值范围为. 为了避免近似计算梯度，上述公式中的第二条项链规则需要计算梯度 矩阵在做了以下近似之后，下面的算法流程图总结了本文的训练方法

4 实验结果

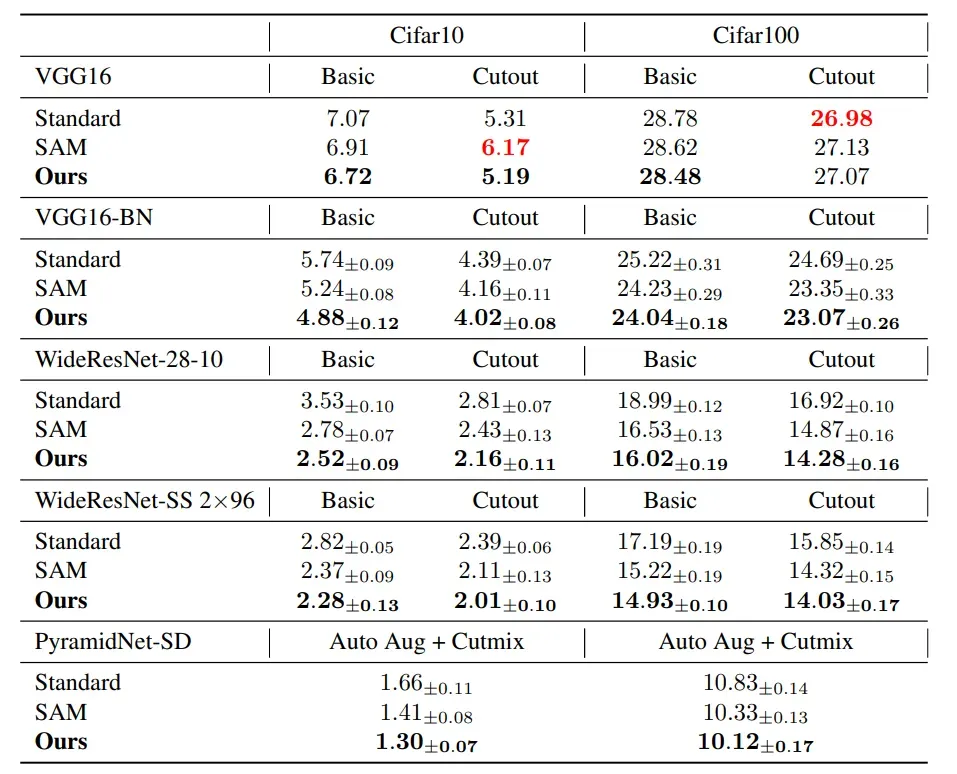
下表显示了两个数据集中具有不同网络结构的三种训练方法之间的测试错误率比较 和 标准培训， 以及本文中的梯度约束。可以直观地发现，在大多数情况下，本文提出的方法的测试错误率最低，这也证明了本文方法的训练可以提高测试的泛化能力 模型

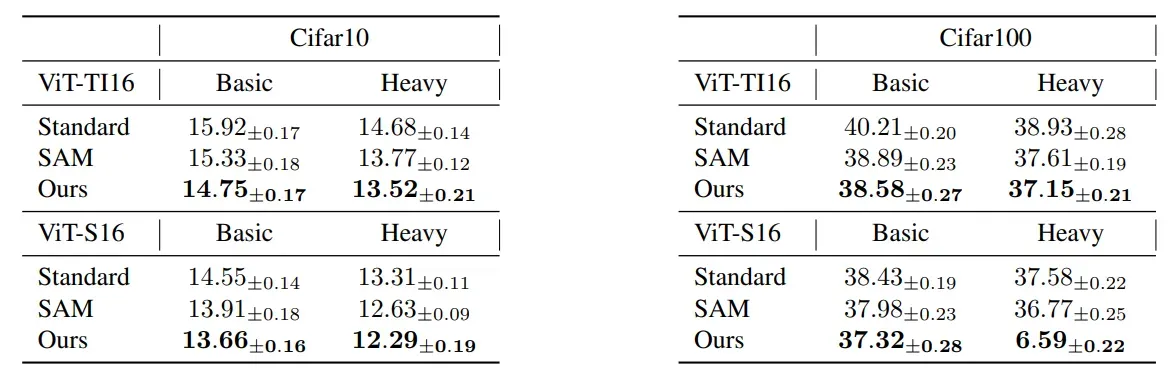
本文作者还在当前非常流行的网络结构中进行了实验。下表显示了三种不同训练方法的测试错误率比较 两个数据集中的网络结构 和 以及本文中的梯度约束。同样，可以发现，本文提出的方法的测试错误率在所有情况下都是最低的，这表明本文的方法也可以提到 模型