1. AI技术聚合首页
  2. 技术文章

深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)

社会演员多 • • 技术文章 • 阅读 1355

前言

激活函数是添加到人工神经网络的函数，类似于人脑中基于神经元的模型，它最终决定向下一个神经元发射什么。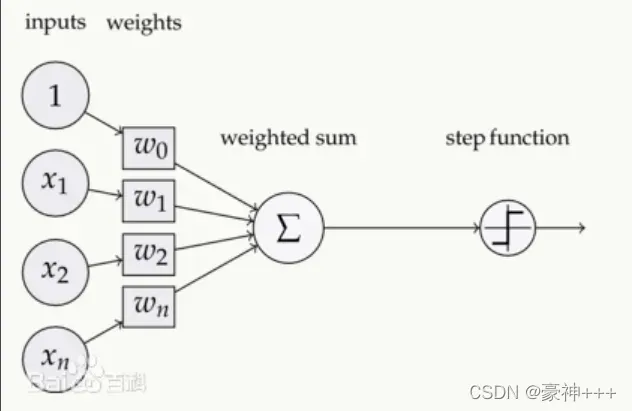
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)
此图来自百度百科，其中step function就是激活函数，它是对之前一层进行汇总后信号进行激活，传给下一层神经元。
常用的激活函数有以下8个：

常用的8个激活函数

  1. Sigmoid
  2. Tanh
  3. ReLU
  4. Softmax
  5. Leaky ReLU
  6. ELU
  7. PReLU
  8. Swish

1. Sigmoid

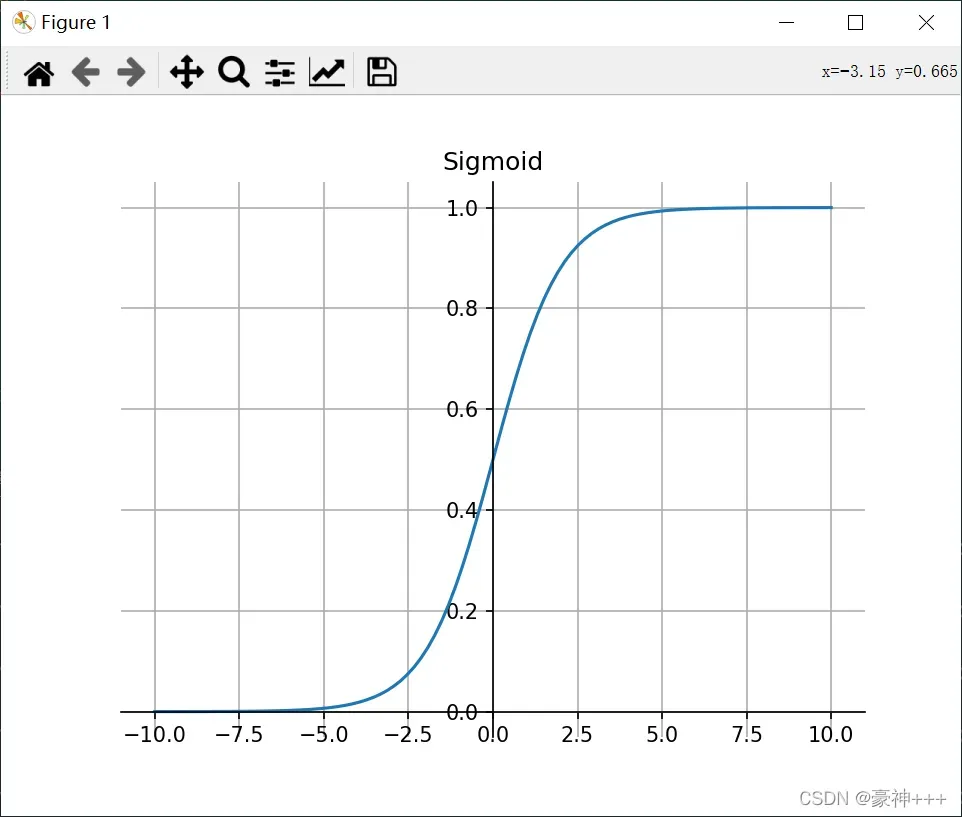
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)

如上图是Sigmoid函数的函数图像。

Sigmoid 函数的图像看起来像一个 S 形曲线。

公式：
f%28x%29%3D%5Cfrac%201%7B1%2Be%5E%7B-x%7D%7D
特征：

  1. Sigmoid 函数的输出范围是 0 到 1。由于输出值在 0 到 1，所以它可以对每个神经元的输出进行了归一化。
  2. 因为Sigmoid 函数的输出范围是 0 到 1，所以可以用于将预测概率作为输出的模型。
  3. 梯度平滑以避免跳跃输出值。
  4. 容易渐变消失。
  5. 函数输出不是以 0 为中心的，这会降低权重更新的效率。
  6. Sigmoid 函数是指数运算，计算机运行得较慢。

代码演示：

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = sigmoid(x)

ax.plot(x, y)
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Sigmoid")
plt.show()

2. Tanh

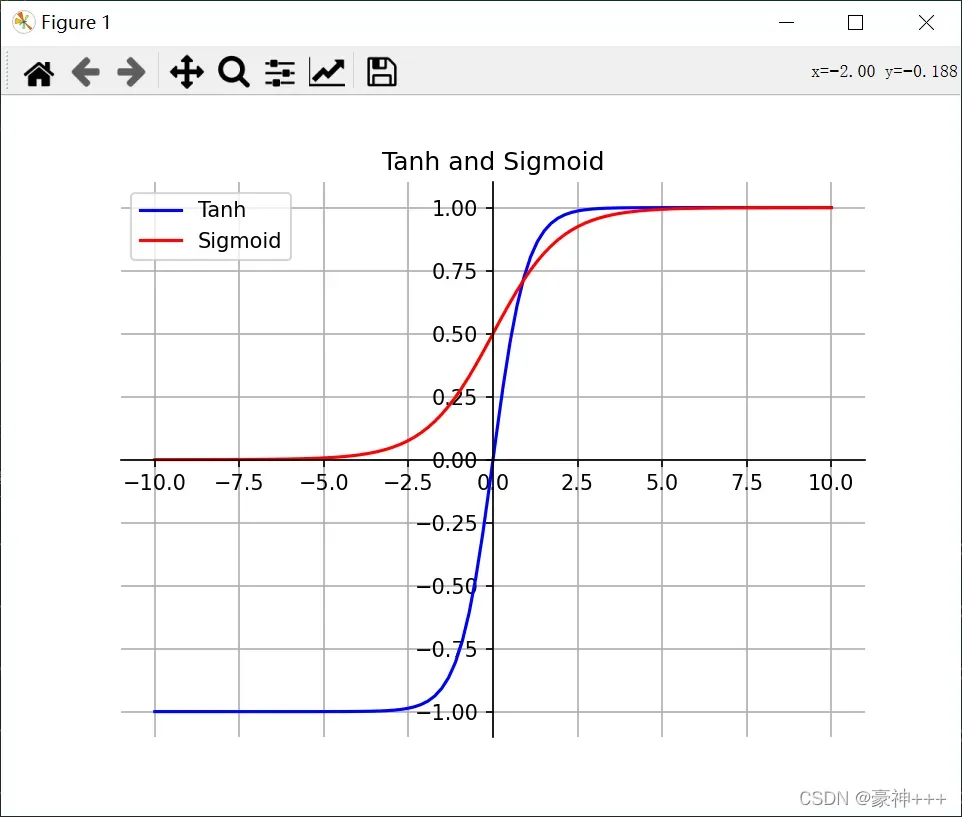
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)
如上图是Tanh函数的函数图像。

Tanh 函数的图像看起来像一个有点扁的 S 形曲线。Tanh 是一个双曲正切函数。Tanh 函数和 Sigmoid 函数的曲线相对相似。但是它比 Sigmoid 函数更有一些优势。

公式：
f%28x%29%3D%5Cfrac%202%7B1%2Be%5E%7B-2x%7D%7D-1
特征：

  1. 首先，当输入较大或较小时，输出几乎是平滑的并且梯度较小，这不利于权重更新。二者的区别在于输出间隔，Tanh 的输出间隔为 1，并且整个函数以 0 为中心，比 Sigmoid 函数更好。
  2. 在 Tanh 图中，负数信号输入，输出也是负数信号。
  3. 在一般的二元分类问题中，Tanh 函数用于隐藏层，而 Sigmoid 函数用于输出层，但这并不是固定的，需要根据特定问题进行调整。
    代码演示：

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def tanh(x):
    return 2 / (1 + np.exp(-2*x)) - 1

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y1 = tanh(x)

y2 = sigmoid(x)

ax.plot(x, y1, '-b', label='Tanh')
ax.plot(x, y2, '-r', label='Sigmoid')
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Tanh and Sigmoid")
plt.show()

3. ReLU

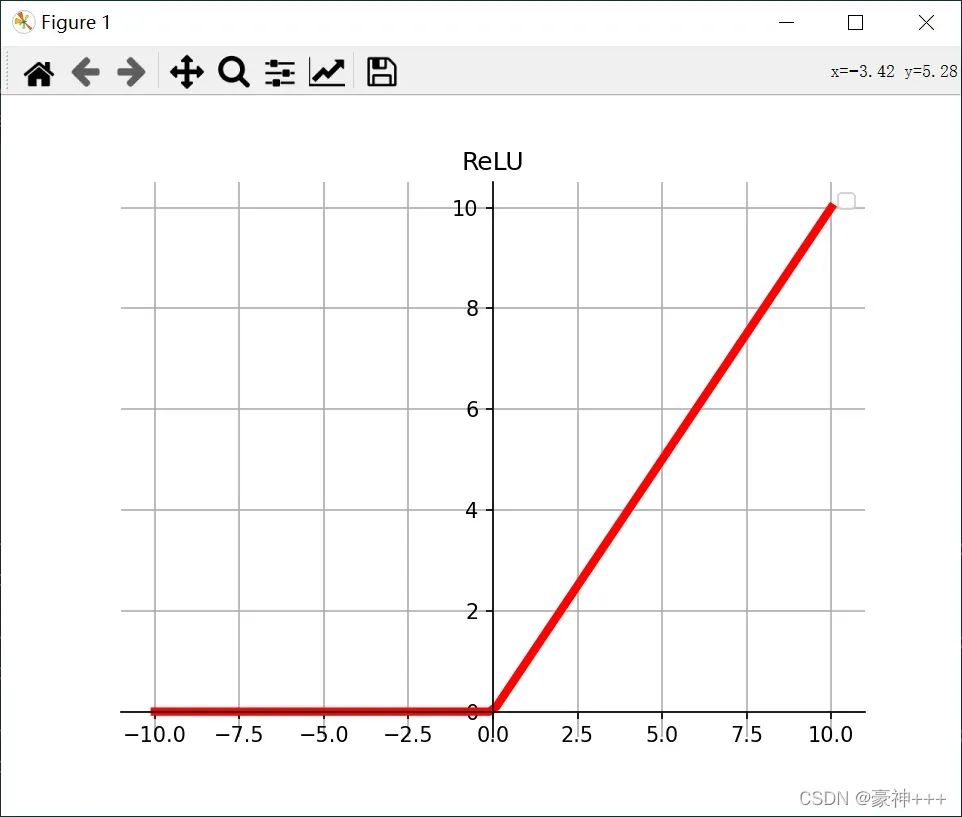
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)

如上图是ReLU函数的函数图像。

ReLU 函数是深度学习中较为流行的一种激活函数。

公式：
f%28x%29%3D%20%5Cbegin%7Bcases%7D%20%7Bmax%280%2C%20x%29%7D%26%5Ctext%7Bx%20%E2%89%A5%200%7D%5C%5C%200%26%20%5Ctext%7Bx%20%3C%200%7D%20%5Cend%7Bcases%7D
特征：

  1. 当输入为正时，不存在梯度饱和问题。
  2. 计算速度快。ReLU 函数中只存在线性关系，因此它的计算速度比 sigmoid 和 tanh 更快。
  3. 当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。有些区域很敏感，有些则不敏感。但是在反向传播过程中，如果输入负数，则梯度将完全为零。
    代码演示：

import matplotlib.pyplot as plt
import numpy as np

def relu(x):
    return np.maximum(0, x)

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = relu(x)
ax.plot(x, y, '-r', linewidth=4)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("ReLU")
plt.show()

4. Softmax

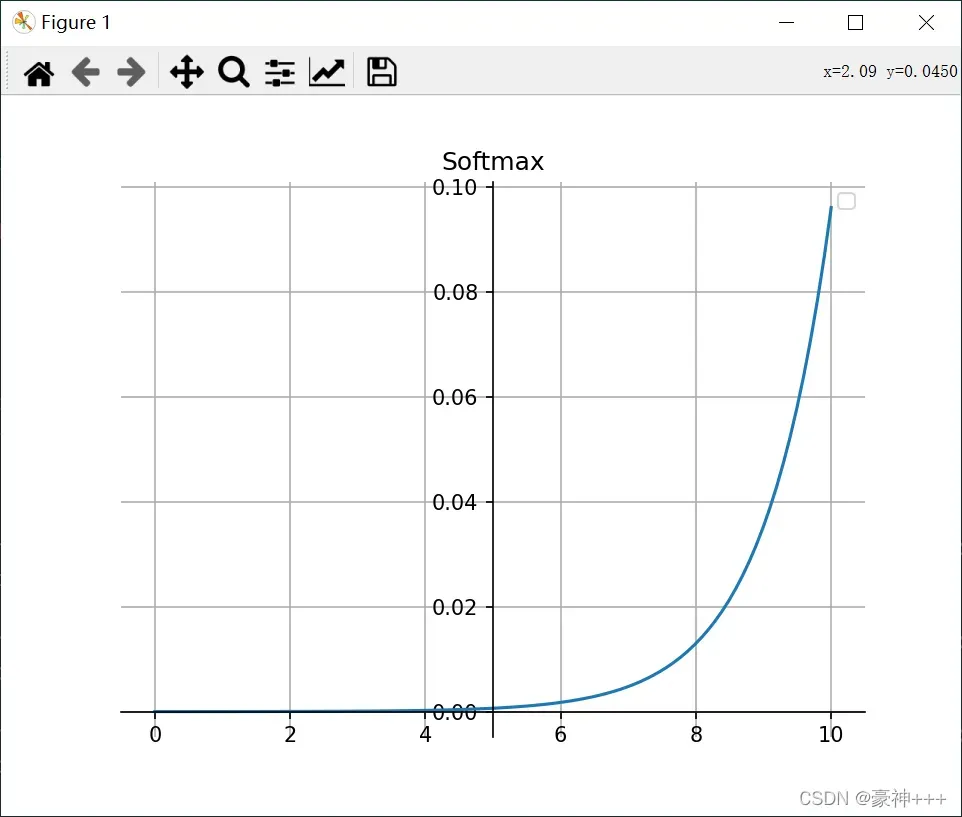
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)
如上图是Softmax函数的函数图像。

公式：
%5Cfrac%20%7Be%5E%7Bx_i%7D%7D%7B%5Csum_%7Bj%3D1%7D%5Ene%5E%7Bx_j%7D%7D
特征：

  1. 在零处不可微。
  2. 负信号输入的梯度为零，这意味着对于该区域的激活，在反向传播期间权重不会更新，从而产生永远不会激活的死神经元。
  3. Softmax 函数的分母结合了原始输出值的所有因子，这意味着 Softmax 函数获得的各种概率彼此相关，因此Softmax 是用于多类分类问题。

代码演示


import matplotlib.pyplot as plt
import numpy as np

def softmax(x):
    x = np.exp(x) / np.sum(np.exp(x))
    return x
fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = softmax(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Softmax")
plt.show()

5. Leaky ReLU

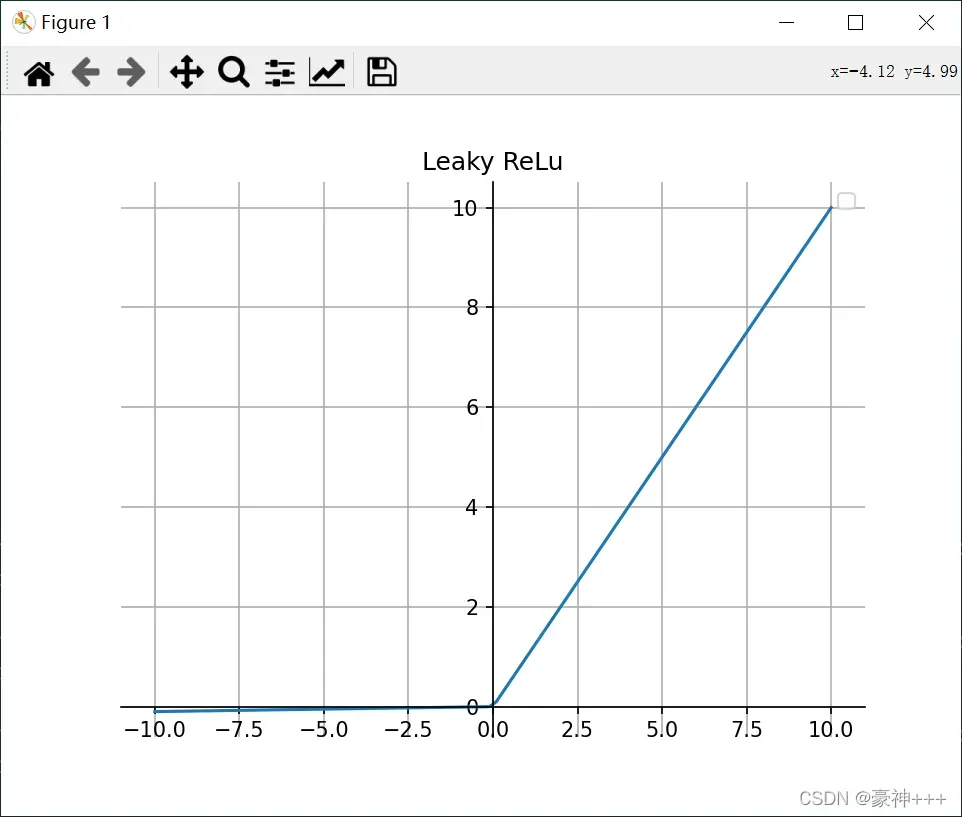
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)
如上图是Leaky ReLU函数的函数图像。

它是一种专门设计用于解决 ReLU 梯度消失问题的激活函数。

公式：
f%28x%29%3D%20%5Cbegin%7Bcases%7D%20%7Bx%7D%26%5Ctext%7Bx%20%E2%89%A5%200%7D%5C%5C%20%7Bax%7D%26%20%5Ctext%7Bx%20%3C%200%7D%20%5Cend%7Bcases%7D
特征：

  1. Leaky ReLU 通过把 x 的非常小的线性分量给予负数信号来调整负值的零梯度问题。
  2. leak 有助于扩大 ReLU 函数的范围，通常 a 的值为 0.01 左右。

注意： 从理论上讲，Leaky ReLU 具有 ReLU 的所有优点，而且 Dead ReLU 不会有任何问题，但在实际操作中，尚未完全证明 Leaky ReLU 总是比 ReLU 更好。

代码演示：


import matplotlib.pyplot as plt
import numpy as np

def leaky_relu(x,a=0.01):
    return np.maximum(a*x, x)
    
fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = leaky_relu(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Leaky ReLu")
plt.show()

6. ELU

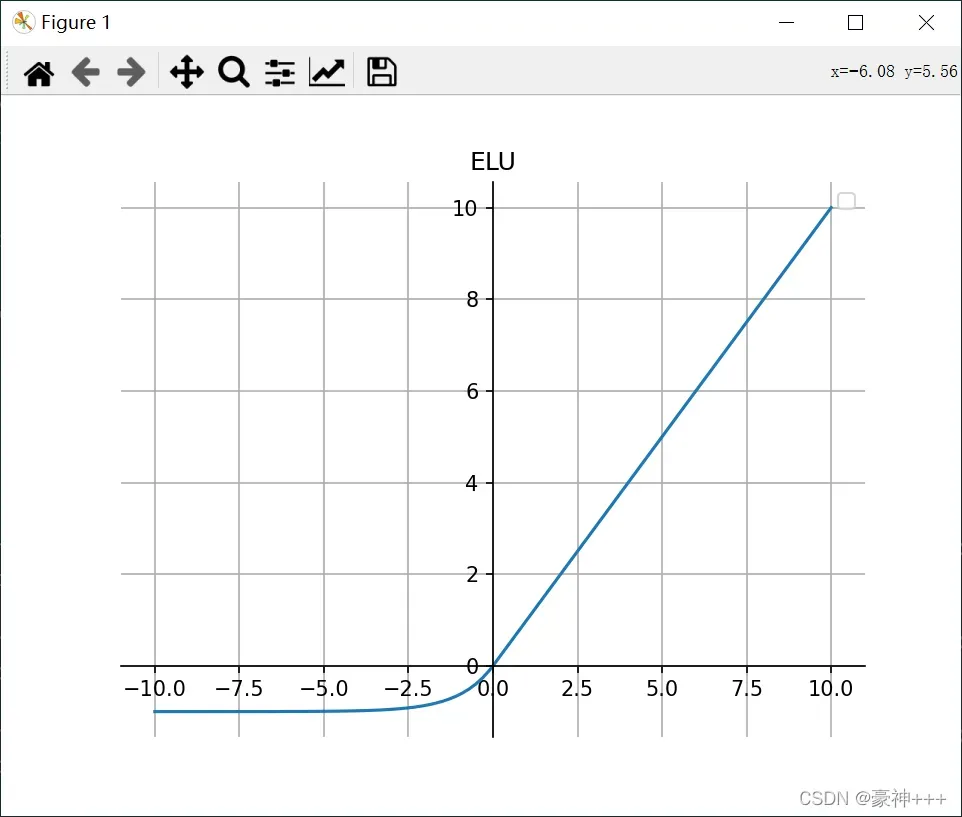
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)

如上图是ELU函数的函数图像。

ELU 的提出也解决了 ReLU 的问题。与 ReLU 相比，ELU 有负值，这会使激活的平均值接近零。均值激活接近于零可以使学习更快，因为它们使梯度更接近自然梯度。

公式：
f%28x%29%3D%20%5Cbegin%7Bcases%7D%20%7Bx%7D%26%5Ctext%7Bx%20%E2%89%A5%200%7D%5C%5C%20%7B%5Calpha%28e%5Ex%20-%201%29%7D%26%20%5Ctext%7Bx%20%3C%200%7D%20%5Cend%7Bcases%7D
特征：

  1. ELU 通过减少偏置偏移的影响，使正常梯度更接近于单位自然梯度，从而使均值向零加速学习。
  2. ELU 在较小的输入下会饱和至负值，从而减少前向传播的变异和信息。

注意： 它的计算强度更高。与 Leaky ReLU 类似，尽管理论上比 ReLU 要好，但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。

代码演示：


import matplotlib.pyplot as plt
import numpy as np
    
def elu(x,alpha=1):
    a = x[x>0]
    b = alpha*(np.exp(x[x<0])-1)
    result=np.concatenate((b,a),axis=0)
    return result

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = elu(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("ELU")
plt.show()

7. PReLU

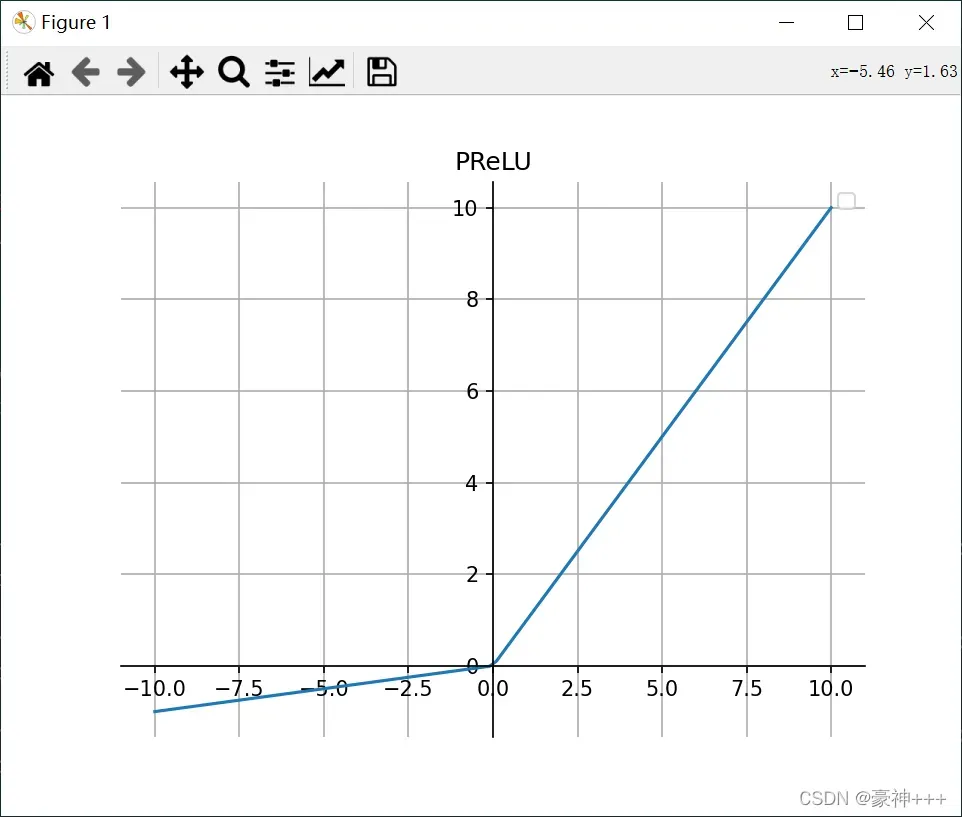
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)
PReLU 也是 ReLU 的改进版本。

公式：
f%28x%29%3D%20%5Cbegin%7Bcases%7D%20%7Bx%7D%26%5Ctext%7Bx%20%E2%89%A5%200%7D%5C%5C%20%7B%5Calpha%20x%7D%26%20%5Ctext%7Bx%20%3C%200%7D%20%5Cend%7Bcases%7D
若%5Calpha是可学习的参数，则f%28x%29变为 PReLU。
特征：

  1. 与 ELU 相比，PReLU 在负值域是线性运算。尽管斜率很小，但不会趋于 0。

代码就不演示了，和上面得Leaky ReLU一样。

8. Swish

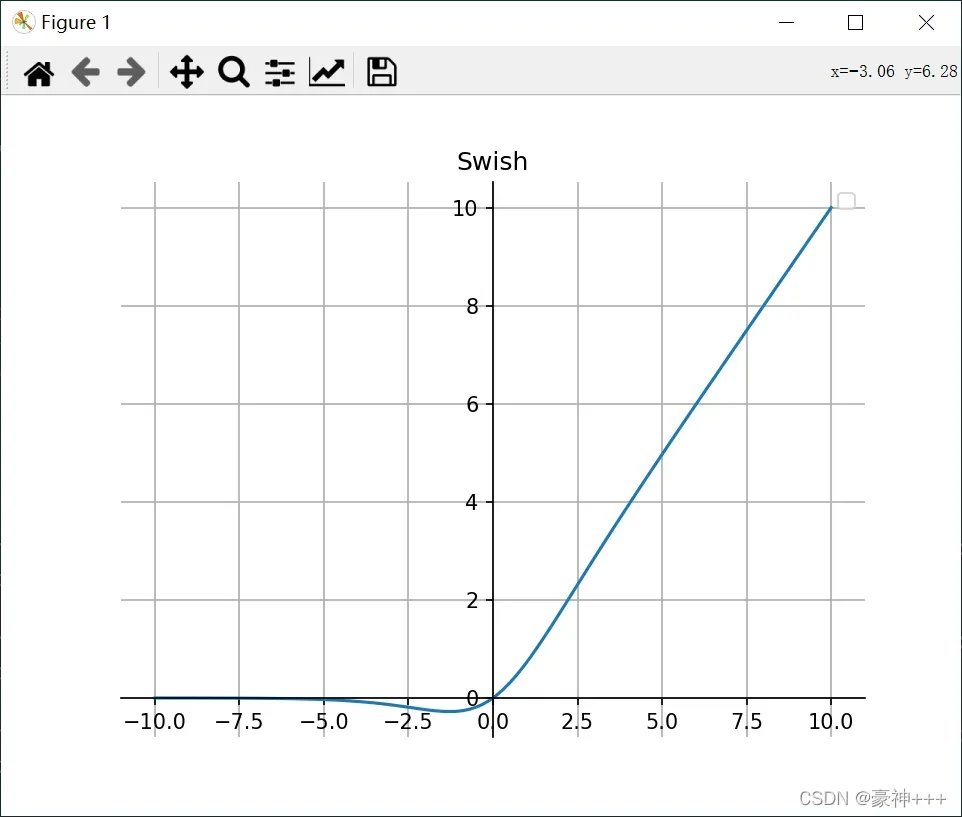
深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish)
如上图是Swish函数的函数图像。

Swish 的设计受到了 LSTM 和高速网络中 gating 的 sigmoid 函数使用的启发。我们使用相同的 gating 值来简化 gating 机制，这称为 self-gating。

self-gating 的优点在于它只需要简单的标量输入，而普通的 gating 则需要多个标量输入。这使得诸如 Swish 之类的 self-gated 激活函数能够轻松替换以单个标量为输入的激活函数（例如 ReLU），而无需更改隐藏容量或参数数量。

公式：
y%20%3D%20x%20%2A%20sigmoid%20%28x%29
特征：

  1. 无界性有助于防止慢速训练期间，梯度逐渐接近 0 并导致饱和；（同时，有界性也是有优势的，因为有界激活函数可以具有很强的正则化，并且较大的负输入问题也能解决）。
  2. 导数总是大于零。
  3. 平滑度在优化和泛化中起着重要作用。

代码演示：


import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def swish(x):
    return sigmoid(x) * x

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = swish(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Swish")
plt.show()

版权声明：本文为博主豪神+++原创文章，版权归属原作者，如果侵权，请联系我们删除！

原文链接：https://blog.csdn.net/qq_42025868/article/details/123066109

共计人评分，平均分

到目前为止还没有投票！成为第一位评论此文章。

赞 (0)
社会演员多的头像社会演员多普通用户
0
上一篇 2022年2月23日 下午6:29
下一篇 2022年2月23日

相关推荐