《 METHODS FOR NON-LINEAR LEASTSQUARES PROBLEMS》论文学习

在传感器误差纠正、SLAM感知、轨迹生成与优化等机器人技术中，最优化理论是极其基本又重要的理论。根据朴素贝叶斯定理，机器人的状态估计问题一般可以转换为求最大似然概率的问题，而最大似然概率问题又可以转换到最小二乘问题上。本篇论文探讨了解决非线性最小二乘问题的一些经典优化方法，例如牛顿法、高斯牛顿法、梯度下降法、LM算法、狗腿算法等。这是一篇比较综合且理解起来不难的论文。我就直接通过这篇论文来入门最优化理论吧。当然后续要系统的看一些经典的书籍

一、基本概念

首先，什么是最小二乘问题？

这个问题在高中数学就学过，最经典的例子就是曲线拟合。我们需要找到一条合适的曲线来拟合给定的坐标，通过每个点到曲线的距离的最小平方和来衡量。我们用数学语言来描述它：

我们把衡量标准用数学语言描述出来，只要距离平方和越小，拟合效果就越好。通过函数表达式，我们发现曲线拟合问题实质上就是找到参数b的取值使得衡量函数的值最小。通过曲线拟合的例子我们引出最小二乘问题的定义。

通过上式我们知道我们的任务就是要找到目标b值，它对应的目标函数最小。我们很自然的想到求一阶导数等于0，求解b。考虑到求导后的式子的美观，所以才在F(b)前加了一个系数项1/2。

非线性和线性最小二乘问题之间的区别？

这里的线性与非线性指的是误差函数f(b)与b的关系，在上面的例子中显然是非线性的。所以是非线性最小二乘问题。

如果我们拟合多项式

显然这里的f(b)与b就是一个线性关系。这就变成了线性最小二乘问题。

本文主要讨论非线性最小二乘问题

关于最小值和局部最小值

解决最小二乘问题的终极目标就是要找到一个自变量b，使得此处的F(b)最小，我们把这个b叫做全局最小点。然而这并不是能偶很容易办到的事情。
首先，对于复杂的F(b)进行求导不一定能成功。即使可以求导，得到的也只是极值，没有很好的办法证明他同时也是最值。如果直接让F(b)=0，也不一定有普适的求解公式。基于以上问题，人们提出了局部最小值和迭代求解的概念。

局部最小值的思路是要求目标函数值在某一个区域内为最小即可。用数学语言描述如下(从这里以后把b替代成习惯性的x)

有了定义后，我们该怎么判断是否是局部最小值呢？我们清楚在局部最小值在小领域内必定有导数等于0.然而导数为零的也可能是局部最大值或者是鞍点（既不是最大值也不是最小值但导数为零），导数等于零处称为驻点。所以我们还需要寻找一个充分条件来判断局部最小值。

假设目标函数F是一个光滑可微的函数，那么他就可以进行泰勒展开

已知在目标点处J=0，那么上式可以化简为：

根据局部最小值的定义，我们知道

所以我们可以得出结论

也就是说，Hessian矩阵必须是一个正定二次矩阵，才能将驻点判断为局部最小值。我们可以总结出以下规则：

2.下降法

下降法是为了保证函数值在迭代解的每一个过程中不断递减。这主要分为两个任务

• 找到下降的方法
• 沿递减方向找到一个步长，使函数的值减小

基于以上原理，我们可以将下降法概括为以下过程：

假设我们在x0这点做下降操作，我们对这一点处附近进行泰勒展开：

根据下降的要求，我们很容易得到一个寻找下降方向的判据

接下来，我们应该确定步长的值，并关心我们在当前下降方向选择哪个步长值以最小化函数值。用数学语言描述为

求解上面问题的过程被称为线搜索。一般在高斯牛顿法和牛顿法中都默认步长为1.关于线搜索我会再写一篇文章讨论它，我们暂时把注意力放在寻找下降方向上，而寻找下降方法有两个非常经典的算法：牛顿法和梯度下降法。

梯度下降

我们可以用一个公式来衡量函数下降了多少

从上式中，我们可以得出当夹角为0，也就是下降方向与梯度一致时，下降程度最大。所以我们可以得到下降方向：

基于上述方法确定下降方向的方法称为梯度下降。下降方向的选择是“最优的”（局部），我们可以将其与准确的线搜索结合起来。此类方法收敛，但最终收敛是线性的并且通常非常缓慢。然而，对于许多问题，该方法在迭代过程的初始阶段具有相当好的性能。

牛顿法

寻找局部最小值点意味着我们需要先找到一阶导等于0的地方。我们把目标点附近进行泰勒展开

然后迭代

假设Hessian矩阵在迭代过程中都是正定的，它必须满足下面的公式（正定矩阵的性质）

也因为

你可以通过替换得到它

这满足了下降的条件，因此我们可以证明hn是一个下降方向。从以上的证明我们知道牛顿法在临近目标点处且附近的海森矩阵为正定时，收敛效果较好。然而当海森矩阵为负定时，牛顿法并不会让迭代朝着函数值下降的方向进行。

混合方法

基于牛顿法，在Hessian矩阵不是正定的地方就不能再进行降序运算了，所以人们自然认为这种情况下可以改用继续降序的方法。因此提出了一种结合牛顿法和梯度下降法的混合方法。如下所示

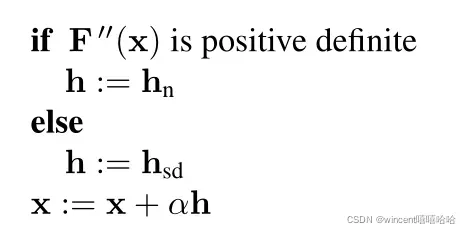
当Hessian矩阵正时，我们继续用牛顿法进行下降操作。当Hessian矩阵为负时，我们使用梯度下降。这样的混合方法非常有效，但也面临一个问题：复杂函数的Hessian矩阵的求解是一项计算量非常大的工作，所以后面我们将继续讨论以下两个问题。

• 混合算法需要满足目标点附近的迭代次数，同时保持连续下降
• 避免陷入 Hessian 矩阵的繁重计算中

3.解决非线性最小二乘问题

回到我们在第 1 章中的讨论，求解非线性最小二乘问题可以用数学语言描述为

牛顿法

我们首先使用牛顿法来解决这个问题，以更好地说明高斯牛顿法和牛顿法的区别。目标点附近一阶导数的泰勒展开

令上式等于0，可以得到牛顿法的下降方向为

由以上三个式子便可以解出牛顿法的下降方向，但我们之前也提到过求f的海塞矩阵通常是不容易的。

高斯-牛顿法

高斯牛顿法是一种基于对误差函数f进行线性化处理的优化方法。所以我们将误差函数进行一阶泰勒展开

注意这里的雅可比矩阵是对误差函数f的一阶导，和对目标函数F的一阶导是不同的

将上式代入目标函数的泰勒展开式，可得

找下降方向的本质就是：选择什么样的h才能让F(x+h)最小。在寻找方向这个步骤中h是自变量，x并不是自变量。问题就变成了解决下面这个局部最小问题

我们求F(x+h)对h的导数并令它等于0可得

我们之前问过

代入上式可以得到高斯-牛顿法的下降方向，也可以表示为

把它和牛顿法求出的下降方向hn比较一下我们可以发现实际上高斯牛顿法的分母省略了带有海塞矩阵的项。可以理解为高斯牛顿法中做了下面的处理

这样做的依据是在目标点附近误差函数接近为0，所以可以省略带海塞矩阵的项，而这样的处理正好避免了计算海塞矩阵的缺点。当然这也表示了这种方法适合在临近目标点附近处的迭代。当初始点距离目标点较远时，这样的方法会失效。

Levenberg-Marquardt算法

LM算法的核心思想是在高斯牛顿法中加入一个阻尼因子来决定迭代时下降的更激进还是更保守。

这个阻尼因子会根据我们定义的指标改变自己的大小

p为增益比，L表示的是对原函数的一阶泰勒近似模型，分子表示真实原函数的下降量，分母表示近似模型的下降量。当p>0时，说明近似模型的下降方向和真实函数减小保持一致，可以接受，并将阻尼因子变小。而p<0时，说明这时的下降方向已经与真实情况不一致了，这时需要增大阻尼因子减小下降的力度。规则如下：

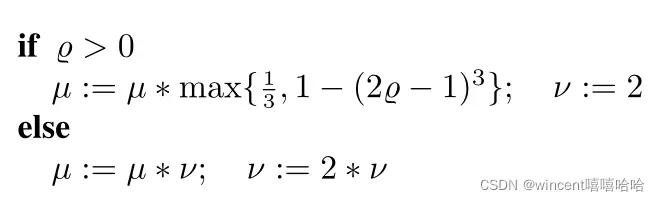
阻尼因子影响着下降方向的选择。它的取值会让LM算法有时倾向于高斯牛顿法，有时倾向于梯度下降法，实现了混合算法对迭代初始阶段和临近目标点时的要求。

当u趋于0时上式变为

当u较大时

使用步长求解方法，现在我们需要迭代停止的条件。

• 一阶导接近0

• 下降步长足够小

• 迭代次数限制

整个算法流程如下：

狗腿

狗腿法也是一种高斯牛顿法和梯度下降法的混合方法。区别于LM算法中的引入的阻尼因子，狗腿法引入了置信区域的概念。在置信区域内，我们认为泰勒一阶展开模型足够精确。因此当置信区域范围较大时，下降的程度倾向于变大，以快速向目标点进发。当置信区域小的时候，就需要我们减小步长一步一步“小心翼翼”的向前进发。

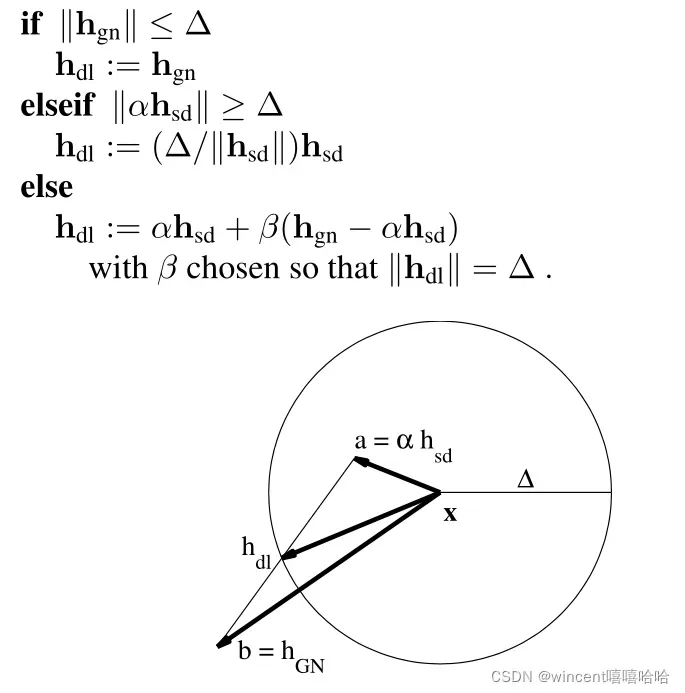
上图是狗腿法选择步长的示意图。其实狗腿法的下降方向与步长选择原则就是尽量x_new 落在置信区域的边缘，尽可能让下降更快且还在置信区域内。

置信区域的大小也是在不停变化的，衡量指标和LM算法的一样。另外迭代停止条件也是一样的。算法流程如下:

4.总结

其实这篇论文在后面还讲到了LM算法与拟牛顿法的混合，以及割线版本的LM算法和狗腿法，但LM算法和狗腿法对我来说就已经够用了，所以后面也没再去详细深究了。

下一步主要是用代码实现LM算法，不得不说最近我的代码能力下降的挺多的。表现在看别人代码看不懂，自己写不知道怎么入手，尤其是这些数学算法。所以talk it easy，show me code。