文章目录
- 一、滤波器简介
- 二、用matlab做巴特沃斯低通滤波器
- 2.1基本数据
- 2.2做出原信号的频谱函数
- 2.3做出巴特沃斯低通滤波器
- 2.4用滤波器过滤信号 并得出频谱图
- 2.5对高频的信号的低通滤波
- 三、MATLAB中filter的理解与使用
- 3.1filter概念与基本语法
- 3.2以最简单的 y = filter(b,a,X) 为例
- 3.3可实现差分方程
- 四、巴特沃斯模拟滤波器(低通,高通,带通,带阻)设计-MATLAB实现
- 4.1基础知识介绍
- 4.2函数介绍
- 4.2.1buttord – 求解滤波器的阶数N和3dB截止频率wc
- 4.2.2butter – 求解N阶滤波器的具体参数B和A,求解完B和A后滤波器就设计完成了
- 4.2.3filter – 滤波函数
- 4.3代码实现
- 4.3.1低通滤波器
- 4.3.2高通滤波器
- 4.3.3带通滤波器
- 4.3.4带阻滤波器
- 五、OpenCV-巴特沃斯低通&高通滤波器(C++)
一、滤波器简介
1.低通滤波器
低通滤波是将频域图像中的高频部分滤除而通过低频部分。图像的边缘和噪声对应于频域图像中的高频部分,而低通滤波的作用即是减弱这部分的能量,从而达到图像平滑去噪的目的。
2.理想低通滤波器
最简单的低通滤波器是理想低通滤波器,基本思想是给定一个频率阈值,将高于该阈值的所有部分设置为0,而低于该频率的部分保持不变。
二、用matlab做巴特沃斯低通滤波器
趁着暑假,做一个心电图的matlab实验,遇到了滤波器问题,网上代码比较杂乱,做了一个汇总整理。
主要做了一个简单的低通滤波器并以三角函数为例子进行低通滤波。
2.1基本数据
fk=100 %采样频率
N=1024 %采样个数
n=-N/2:N/2-1
f=n*fk/N
t=n/fk
y=sin(2*pi*10*t)
当然 f也可以表示成 f=linspace(-fk/2,fk/2,N);
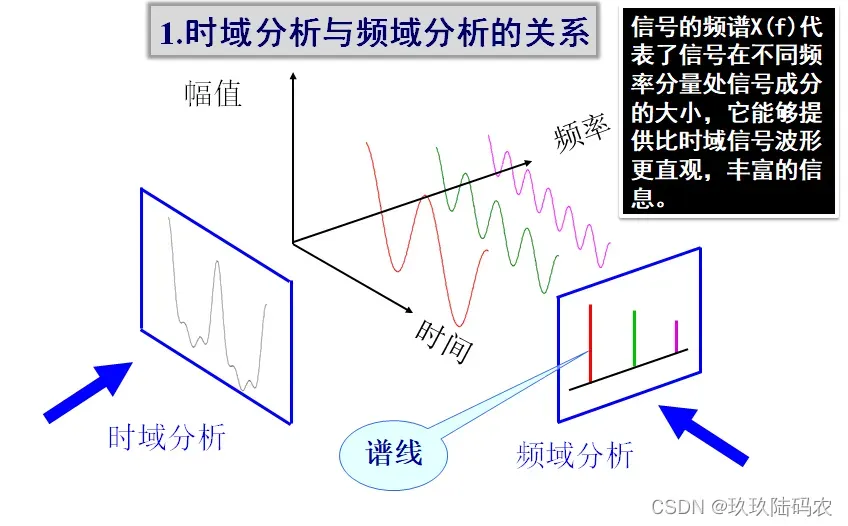
2.2做出原信号的频谱函数
注意:用fft函数作频谱分析,得到的是0~fk内的频谱
而用fftshift函数得到-fk/2~fk/2内的频谱
fft_y=fft(y);
fftshift_y=fftshift(fft_y);
f=linspace(-50,50,1024);
plot(f,abs(fftshift_y));
2.3做出巴特沃斯低通滤波器
【1】用buttord函数求出阶数以及Wn
butter函数是求Butterworth数字滤波器的系数,在求出系数后对信号进行滤波时用filter函数
[g,Wn]=buttord(Wp,ws,Rp,Rs);
Wp=fp/(0.5fk)=20/50=0.4(通带截至频率)
Ws=fs/(0.5*fk)=30/50=0.6(阻带截止频率)
Rp=1; 通带最大衰减
Rs=30; 阻带最小衰减
代码如下:
[g,Wn]=buttord(0.4,0.6,1,30);
【2】用butter 求出差分方程的系数b a
不懂差分方程及filter用法的朋友可以点以下链接
[b,a]=butter(g,Wn);
至此 准备工作都做完了 ,来看看这滤波器的相频特性啥样子
【3】滤波器的相频特性
[q,w]=freqz(b,a,256);
plot(w*fs/(2*pi),abs(q))
所以说 咱写出来的滤波器长这个样子
20Hz为通带截至频率
30Hz为阻带截至频率
2.4用滤波器过滤信号 并得出频谱图
用filter过滤
用filter函数就能把原信号y过滤成k函数 ,需要注意的是,它们都是时域函数,需要进行fft变换才能看到频谱图
k=filter(b,a,y);
fft_k=fft(k);
fftshift_k=fftshift(fft_k);
plot(f,abs(fftshift_k));
过滤后的结果如下:
没错,没变!我们低通滤波器允许20Hz以下的信号不变,而我们原信号的频率就是10Hz!
2.5对高频的信号的低通滤波
这里就不赘述了,对y=sin(2pi40*t)的信号,依然用上面的低通过滤的结果如下图:
不要看它长的怪,注意一下幅值,约等于0,即把40Hz的信号过滤掉了!
三、MATLAB中filter的理解与使用
3.1filter概念与基本语法
filter函数是一维的数字滤波器,主要的应用语法如下所示
y = filter(b,a,X)
[y,zf] = filter(b,a,X)
[y,zf] = filter(b,a,X,zi)
y = filter(b,a,X,zi,dim)
[…] = filter(b,a,X,[],dim)
3.2以最简单的 y = filter(b,a,X) 为例
y = filter(b,a,X) 滤除向量X中的数据,其中b是分子系数向量,a是分母系数向量。如果a(1)不等于1的话,则就利用a(1)标准化滤波器系数,可以利用多项式除法使分母变为1;如果 a(1) 等于0,滤波器返回错误值。
3.3可实现差分方程
Y = FILTER(B,A,X) ,输入X为滤波前序列,Y为滤波结果序列,B/A 提供滤波器系数,B为分子, A为分母
整个滤波过程是通过下面差分方程实现的:
a(1)*y(n) = b(1)*x(n) + b(2)*x(n-1) + … + b(nb+1)*x(n-nb)-a(2)*y(n-1) - a(3)*y(n-2) + … + a(nb+1)*y(n-nb)
例:
filter([1,2],1,[1,2,3,4,5])
实现 y[k]=x[k]+2*x[k-1]
括号中向量b为x[k]、x[k-1]、…的系数,向量a为y[k]、y[k-1]、…的系数。
x为需要滤波的向量,y为滤波后的向量(显然,x和y的长度是一样的,看后面例子就知道了)。
举个例子来说明filter的原理,如下:
a = [1 2];
b = [2 3];
x = [1 2 3 4 5 6];
y = filter(b, a, x)
y =
2 3 6 5 12 3
下面给出具体的计算过程如下:
a(1)y(1) = b(1)x(1); %可以求出y(1)
a(1)y(2) = b(1)x(2)+b(2)x(1) –a(2)y(1); %可以由y(1)求出y(2)
a(1)y(3) = b(1)x(3)+b(2)x(2)-a(2)y(2); %可以由y(2)求出y(3)
a(1)y(4) = b(1)x(4)+b(2)x(3)-a(2)y(3); %可以由y(3)求出y(4)
a(1)y(5) = b(1)x(5)+b(2)x(4)-a(2)y(4); %可以由y(4)求出y(5)
a(1)y(6) = b(1)x(6)+b(2)x(5)-a(2)y(5); %可以由y(5)求出y(6)
计算结束,得到y(n)(n=1、2、…、6)
目前就暂且记到这里
四、巴特沃斯模拟滤波器(低通,高通,带通,带阻)设计-MATLAB实现
4.1基础知识介绍
4.2函数介绍
首先介绍一些用到的MATLAB函数
4.2.1buttord – 求解滤波器的阶数N和3dB截止频率wc
[N,wc] = buttord(wp, ws, Rp, As, ‘s’)
输入参数如下:
通带边界模拟频率wp、阻带边界模拟频率ws(模拟角频率,单位是rad/s)
通带最大衰减Rp、阻带最小衰减As(单位是dB)
‘s’指的就是模拟滤波器,设计数字滤波器时就没有’s’这个参数了。
4.2.2butter – 求解N阶滤波器的具体参数B和A,求解完B和A后滤波器就设计完成了
[B,A] = butter(N, wc, ‘ftype’, ‘s’) - 模拟滤波器设计
输入参数如下:
N – 滤波器阶数
wc – 3dB截止模拟频率(单位rad/s,N和wc都是用buttord函数计算出来的)
ftype – 滤波器类型‘’:
(1)当输入wc为一维向量时:
默认情况下设计的低通滤波器,设计高通滤波器的话令ftype=high
(2)当输入wc为二维向量[wcl,wcu]时:
默认情况下设计的带通滤波器,设计带阻滤波器的话令ftype=stop
4.2.3filter – 滤波函数
y = filter(B,A,x)
这个就是滤波函数了,
x是输入的有噪声的信号,
B,A就是设计好的滤波器参数
得到的输出y就是滤波后的信号了。
4.3代码实现
4.3.1低通滤波器
例: 设计通带截止频率5kHz,通带衰减2dB,阻带截止频率12kHz,阻带衰减30dB的巴特沃斯低通滤波器
由题可知,设计的是模拟滤波器,所以用到下面三个函数:
[N,wc] = buttord(wp, ws, Rp, As, ‘s’)
[B,A] = butter(N, wc, ‘ftype’, ‘s’)
y = filter(B,A,x)
代码如下:
wp = 2 * pi * 5000;
ws = 2 * pi * 12000;
Rp = 2;
As = 30;
[N, wc] = buttord(wp, ws, Rp, As, 's');
[B, A] = butter(N, wc, 's');
上面这些代码就设计好了滤波器
如果有输入噪声信号x的话,调用y = filter(B,A,x),得到的y就是滤波后的信号了。
下面是绘图部分
为了让滤波器的结果得到更形象的表示,我们可以画出来它的幅频特性曲线,代码如下:
其中,我们使用了freqs这个函数,
h = freqs(B,A,wk)
它是用来计算当频率为wk时,对应的频率响应h的大小,主要是用来画图的。
绘图代码如下:
f = 0 : 10 : 14000;%取点,从0-14000,每隔10取一个点
w = 2 * pi * f;%注意模拟滤波器用的频率都是模拟角频率,要乘上2pi的
Hk = freqs(B,A,w);%对于取的每个点,求该处的频率响应大小
%画图
figure
plot(f/1000, 20 * log10(abs(Hk)));%横坐标单位是kHz,纵坐标单位是dB,
grid on;
%设置横纵坐标标签
xlabel('f/kHz');
ylabel('-A(f)/dB');
%设置横纵坐标轴范围
axis([0, 14, -40, 5]);
绘图结果如下:
4.3.2高通滤波器
高通滤波器与低通几乎完全一样,只要注意
[B,A] = butter(N, wc, ‘ftype’, ‘s’)中的 ftype=high
例: 设计通带截止频率4kHz,通带衰减0.1dB,阻带截止频率1kHz,阻带衰减40dB的巴特沃斯高通滤波器
代码如下:
wp = 2 * pi * 4000;
ws = 2 * pi * 1000;
Rp = 0.1;
As = 40;
[N, wc] = buttord(wp, ws, Rp, As, 's');
[B, A] = butter(N, wc,'high', 's');%注意这个'high'
高通滤波器设计完成了
如果有输入噪声信号x的话,调用 y = filter(B,A,x),得到的y就是滤波后的信号了。
接着我们画出高通滤波器的幅频特性曲线
f = 0 : 10 : 14000;%取点,从0-14000,每隔10取一个点
w = 2 * pi * f;%注意模拟滤波器用的频率都是模拟角频率,要乘上2pi的
Hk = freqs(B,A,w);%对于取的每个点,求该处的频率响应大小
%画图
figure
plot(f/1000, 20 * log10(abs(Hk)));%横坐标单位是kHz,纵坐标单位是dB,
grid on;
%设置横纵坐标标签
xlabel('f/kHz');
ylabel('-A(f)/dB');
%设置横纵坐标轴范围
axis([0, 14, -60, 5]);
曲线图如下:
4.3.3带通滤波器
例: 设计巴特沃斯带通滤波器,通带上下边界频率分别为4kHz和7kHz,通带衰减1dB,阻带上下边界频率2kHz和9kHz,阻带衰减20dB。
滤波器设计代码如下:
%带通
wp = 2 * pi * [4000, 7000];
ws = 2 * pi * [2000,9000];
Rp = 1;
As = 20;
[N, wc] = buttord(wp, ws, Rp, As, 's');%此时输入wp和ws都是二维的,输出wc也是两维的
[B, A] = butter(N, wc,'s');
带通模拟滤波器设计完成了
如果有输入噪声信号x的话,调用y = filter(B,A,x),得到的y就是滤波后的信号了。
接着我们画出带通滤波器的幅频特性曲线,如下:
f = 0 : 10 : 14000;%取点,从0-14000,每隔10取一个点
w = 2 * pi * f;%注意模拟滤波器用的频率都是模拟角频率,要乘上2pi的
Hk = freqs(B,A,w);%对于取的每个点,求该处的频率响应大小
%画图
figure
plot(f/1000, 20 * log10(abs(Hk)));%横坐标单位是kHz,纵坐标单位是dB,
grid on;
%设置横纵坐标标签
xlabel('f/kHz');
ylabel('-A(f)/dB');
%设置横纵坐标轴范围
axis([0, 14, -60, 5]);
曲线图如下:
4.3.4带阻滤波器
例: 设计巴特沃斯带阻滤波器,通带上下边界频率分别为2kHz和9kHz,通带衰减1dB,阻带上下边界频率4kHz和7kHz,阻带衰减20dB。
%带阻
wp = 2 * pi * [2000, 9000];
ws = 2 * pi * [4000,7000];
Rp = 1;
As = 20;
[N, wc] = buttord(wp, ws, Rp, As, 's');%此时输入wp和ws都是二维的,输出wc也是两维的
[B, A] = butter(N, wc,'stop','s');
带阻模拟滤波器设计完成了,如果有输入噪声信号x的话,调用
y = filter(B,A,x),得到的y就是滤波后的信号了。
接着我们画出带阻滤波器的幅频特性曲线,代码如下:
f = 0 : 10 : 14000;%取点,从0-14000,每隔10取一个点
w = 2 * pi * f;%注意模拟滤波器用的频率都是模拟角频率,要乘上2pi的
Hk = freqs(B,A,w);%对于取的每个点,求该处的频率响应得下
%画图
figure
plot(f/1000, 20 * log10(abs(Hk)));%横坐标单位是kHz,纵坐标单位是dB,
grid on;
%设置横纵坐标标签
xlabel('f/kHz');
ylabel('-A(f)/dB');
%设置横纵坐标轴范围
axis([0, 14, -100, 5]);
结果如下:
五、OpenCV-巴特沃斯低通&高通滤波器(C++)
作者:翟天保Steven
版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处
场景需求
做图像处理,滤波是家常便饭,今天给大家分享巴特沃斯滤波器实现。
众所周知,在频谱中,低频主要对应图像在平滑区域的总体灰度级分布,高频对应图像细节部分,如边缘和噪声。巴特沃斯滤波器被称作最大平坦滤波器。其特点是通频带内的频率响应曲线最大限度平坦,没有纹波,而在阻频带则逐渐下降为零,公式和具体原理就不再罗列了,百度一下全都有,接下来是硬货——C++&OpenCV代码实现。
相关功能函数的C++实现代码
// 巴特沃斯低通滤波核函数
cv::Mat butterworth_low_kernel(cv::Mat &scr, float sigma, int n)
{
cv::Mat butterworth_low_pass(scr.size(), CV_32FC1); //,CV_32FC1
float D0 = sigma;//半径D0越小,模糊越大;半径D0越大,模糊越小
for (int i = 0; i < scr.rows; i++) {
for (int j = 0; j < scr.cols; j++) {
float d = sqrt(pow(float(i - scr.rows / 2), 2) + pow(float(j - scr.cols / 2), 2));//分子,计算pow必须为float型
butterworth_low_pass.at<float>(i, j) = 1.0f / (1.0f + pow(d / D0, 2 * n));
}
}
return butterworth_low_pass;
}
// 巴特沃斯低通滤波
cv::Mat butterworth_low_pass_filter(cv::Mat &src, float d0, int n)
{
// H = 1 / (1+(D/D0)^2n) n表示巴特沃斯滤波器的次数
// 阶数n=1 无振铃和负值 阶数n=2 轻微振铃和负值 阶数n=5 明显振铃和负值 阶数n=20 与ILPF相似
cv::Mat padded = image_make_border(src);
cv::Mat butterworth_kernel = butterworth_low_kernel(padded, d0, n);
cv::Mat result = frequency_filter(padded, butterworth_kernel);
return result;
}
// 巴特沃斯高通滤波核函数
cv::Mat butterworth_high_kernel(cv::Mat &scr, float sigma, int n)
{
cv::Mat butterworth_high_pass(scr.size(), CV_32FC1); //,CV_32FC1
float D0 = (float)sigma; // 半径D0越小,模糊越大;半径D0越大,模糊越小
for (int i = 0; i < scr.rows; i++) {
for (int j = 0; j < scr.cols; j++) {
float d = sqrt(pow(float(i - scr.rows / 2), 2) + pow(float(j - scr.cols / 2), 2));//分子,计算pow必须为float型
butterworth_high_pass.at<float>(i, j) =1.0f-1.0f / (1.0f + pow(d / D0, 2 * n));
}
}
return butterworth_high_pass;
}
// 巴特沃斯高通滤波
cv::Mat butterworth_high_pass_filter(cv::Mat &src, float d0, int n)
{
cv::Mat padded = image_make_border(src);
cv::Mat butterworth_kernel = butterworth_high_kernel(padded, d0, n);
cv::Mat result = frequency_filter(padded, butterworth_kernel);
return result;
}
// 频率域滤波
cv::Mat frequency_filter(cv::Mat &scr, cv::Mat &blur)
{
cv::Mat mask = scr == scr;
scr.setTo(0.0f, ~mask);
//创建通道,存储dft后的实部与虚部(CV_32F,必须为单通道数)
cv::Mat plane[] = { scr.clone(), cv::Mat::zeros(scr.size() , CV_32FC1) };
cv::Mat complexIm;
cv::merge(plane, 2, complexIm); // 合并通道 (把两个矩阵合并为一个2通道的Mat类容器)
cv::dft(complexIm, complexIm); // 进行傅立叶变换,结果保存在自身
// 分离通道(数组分离)
cv::split(complexIm, plane);
// 以下的操作是频域迁移
fftshift(plane[0], plane[1]);
// *****************滤波器函数与DFT结果的乘积****************
cv::Mat blur_r, blur_i, BLUR;
cv::multiply(plane[0], blur, blur_r); // 滤波(实部与滤波器模板对应元素相乘)
cv::multiply(plane[1], blur, blur_i); // 滤波(虚部与滤波器模板对应元素相乘)
cv::Mat plane1[] = { blur_r, blur_i };
// 再次搬移回来进行逆变换
fftshift(plane1[0], plane1[1]);
cv::merge(plane1, 2, BLUR); // 实部与虚部合并
cv::idft(BLUR, BLUR); // idft结果也为复数
BLUR = BLUR / BLUR.rows / BLUR.cols;
cv::split(BLUR, plane);//分离通道,主要获取通道
return plane[0];
}
// 图像边界处理
cv::Mat image_make_border(cv::Mat &src)
{
int w = cv::getOptimalDFTSize(src.cols); // 获取DFT变换的最佳宽度
int h = cv::getOptimalDFTSize(src.rows); // 获取DFT变换的最佳高度
cv::Mat padded;
// 常量法扩充图像边界,常量 = 0
cv::copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));
padded.convertTo(padded, CV_32FC1);
return padded;
}
// 实现频域滤波器的网格函数
void getcart(int rows, int cols, cv::Mat &x, cv::Mat &y) {
x.create(rows, cols, CV_32FC1);
y.create(rows, cols, CV_32FC1);
//设置边界
//计算其他位置的值
for (int i = 0; i < rows; ++i) {
if (i <= rows / 2) {
x.row(i) = i;
}
else {
x.row(i) = i - rows;
}
}
for (int i = 0; i < cols; ++i) {
if (i <= cols / 2) {
y.col(i) = i;
}
else {
y.col(i) = i - cols;
}
}
}
// fft变换后进行频谱搬移
void fftshift(cv::Mat &plane0, cv::Mat &plane1)
{
// 以下的操作是移动图像 (零频移到中心)
int cx = plane0.cols / 2;
int cy = plane0.rows / 2;
cv::Mat part1_r(plane0, cv::Rect(0, 0, cx, cy)); // 元素坐标表示为(cx, cy)
cv::Mat part2_r(plane0, cv::Rect(cx, 0, cx, cy));
cv::Mat part3_r(plane0, cv::Rect(0, cy, cx, cy));
cv::Mat part4_r(plane0, cv::Rect(cx, cy, cx, cy));
cv::Mat temp;
part1_r.copyTo(temp); //左上与右下交换位置(实部)
part4_r.copyTo(part1_r);
temp.copyTo(part4_r);
part2_r.copyTo(temp); //右上与左下交换位置(实部)
part3_r.copyTo(part2_r);
temp.copyTo(part3_r);
cv::Mat part1_i(plane1, cv::Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
cv::Mat part2_i(plane1, cv::Rect(cx, 0, cx, cy));
cv::Mat part3_i(plane1, cv::Rect(0, cy, cx, cy));
cv::Mat part4_i(plane1, cv::Rect(cx, cy, cx, cy));
part1_i.copyTo(temp); //左上与右下交换位置(虚部)
part4_i.copyTo(part1_i);
temp.copyTo(part4_i);
part2_i.copyTo(temp); //右上与左下交换位置(虚部)
part3_i.copyTo(part2_i);
temp.copyTo(part3_i);
}
测试代码
#include<iostream>
#include<opencv2/opencv.hpp>
#include<ctime>
using namespace std;
using namespace cv;
cv::Mat butterworth_low_kernel(cv::Mat &scr, float sigma, int n);
cv::Mat butterworth_low_pass_filter(cv::Mat &src, float d0, int n);
cv::Mat butterworth_high_kernel(cv::Mat &scr, float sigma, int n);
cv::Mat butterworth_high_pass_filter(cv::Mat &src, float d0, int n);
cv::Mat frequency_filter(cv::Mat &scr, cv::Mat &blur);
cv::Mat image_make_border(cv::Mat &src);
void fftshift(cv::Mat &plane0, cv::Mat &plane1);
void getcart(int rows, int cols, cv::Mat &x, cv::Mat &y);
Mat powZ(cv::InputArray src, double power);
Mat sqrtZ(cv::InputArray src);
int main(void)
{
Mat test = imread("tangsan.jpg", 0);
float D0 = 50.0f;
float D1 = 5.0f;
Mat lowpass = butterworth_low_pass_filter(test, D0,2);
Mat highpass = butterworth_high_pass_filter(test, D1, 2);
imshow("original", test);
imshow("low pass", lowpass / 255); // lowpass的数据都比较大,0-255,imshow对于float型Mat显示需要除以255
imshow("high pass", highpass / 255); // highpass的数据都比较大,0-255,imshow对于float型Mat显示需要除以255
waitKey(0);
system("pause");
return 0;
}
// 巴特沃斯低通滤波核函数
cv::Mat butterworth_low_kernel(cv::Mat &scr, float sigma, int n)
{
cv::Mat butterworth_low_pass(scr.size(), CV_32FC1); //,CV_32FC1
float D0 = sigma;//半径D0越小,模糊越大;半径D0越大,模糊越小
for (int i = 0; i < scr.rows; i++) {
for (int j = 0; j < scr.cols; j++) {
float d = sqrt(pow(float(i - scr.rows / 2), 2) + pow(float(j - scr.cols / 2), 2));//分子,计算pow必须为float型
butterworth_low_pass.at<float>(i, j) = 1.0f / (1.0f + pow(d / D0, 2 * n));
}
}
return butterworth_low_pass;
}
// 巴特沃斯低通滤波
cv::Mat butterworth_low_pass_filter(cv::Mat &src, float d0, int n)
{
// H = 1 / (1+(D/D0)^2n) n表示巴特沃斯滤波器的次数
// 阶数n=1 无振铃和负值 阶数n=2 轻微振铃和负值 阶数n=5 明显振铃和负值 阶数n=20 与ILPF相似
cv::Mat padded = image_make_border(src);
cv::Mat butterworth_kernel = butterworth_low_kernel(padded, d0, n);
cv::Mat result = frequency_filter(padded, butterworth_kernel);
return result;
}
// 巴特沃斯高通滤波核函数
cv::Mat butterworth_high_kernel(cv::Mat &scr, float sigma, int n)
{
cv::Mat butterworth_high_pass(scr.size(), CV_32FC1); //,CV_32FC1
float D0 = (float)sigma; // 半径D0越小,模糊越大;半径D0越大,模糊越小
for (int i = 0; i < scr.rows; i++) {
for (int j = 0; j < scr.cols; j++) {
float d = sqrt(pow(float(i - scr.rows / 2), 2) + pow(float(j - scr.cols / 2), 2));//分子,计算pow必须为float型
butterworth_high_pass.at<float>(i, j) =1.0f-1.0f / (1.0f + pow(d / D0, 2 * n));
}
}
return butterworth_high_pass;
}
// 巴特沃斯高通滤波
cv::Mat butterworth_high_pass_filter(cv::Mat &src, float d0, int n)
{
cv::Mat padded = image_make_border(src);
cv::Mat butterworth_kernel = butterworth_high_kernel(padded, d0, n);
cv::Mat result = frequency_filter(padded, butterworth_kernel);
return result;
}
// 频率域滤波
cv::Mat frequency_filter(cv::Mat &scr, cv::Mat &blur)
{
cv::Mat mask = scr == scr;
scr.setTo(0.0f, ~mask);
//创建通道,存储dft后的实部与虚部(CV_32F,必须为单通道数)
cv::Mat plane[] = { scr.clone(), cv::Mat::zeros(scr.size() , CV_32FC1) };
cv::Mat complexIm;
cv::merge(plane, 2, complexIm); // 合并通道 (把两个矩阵合并为一个2通道的Mat类容器)
cv::dft(complexIm, complexIm); // 进行傅立叶变换,结果保存在自身
// 分离通道(数组分离)
cv::split(complexIm, plane);
// 以下的操作是频域迁移
fftshift(plane[0], plane[1]);
// *****************滤波器函数与DFT结果的乘积****************
cv::Mat blur_r, blur_i, BLUR;
cv::multiply(plane[0], blur, blur_r); // 滤波(实部与滤波器模板对应元素相乘)
cv::multiply(plane[1], blur, blur_i); // 滤波(虚部与滤波器模板对应元素相乘)
cv::Mat plane1[] = { blur_r, blur_i };
// 再次搬移回来进行逆变换
fftshift(plane1[0], plane1[1]);
cv::merge(plane1, 2, BLUR); // 实部与虚部合并
cv::idft(BLUR, BLUR); // idft结果也为复数
BLUR = BLUR / BLUR.rows / BLUR.cols;
cv::split(BLUR, plane);//分离通道,主要获取通道
return plane[0];
}
// 图像边界处理
cv::Mat image_make_border(cv::Mat &src)
{
int w = cv::getOptimalDFTSize(src.cols); // 获取DFT变换的最佳宽度
int h = cv::getOptimalDFTSize(src.rows); // 获取DFT变换的最佳高度
cv::Mat padded;
// 常量法扩充图像边界,常量 = 0
cv::copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));
padded.convertTo(padded, CV_32FC1);
return padded;
}
// 实现频域滤波器的网格函数
void getcart(int rows, int cols, cv::Mat &x, cv::Mat &y) {
x.create(rows, cols, CV_32FC1);
y.create(rows, cols, CV_32FC1);
//设置边界
//计算其他位置的值
for (int i = 0; i < rows; ++i) {
if (i <= rows / 2) {
x.row(i) = i;
}
else {
x.row(i) = i - rows;
}
}
for (int i = 0; i < cols; ++i) {
if (i <= cols / 2) {
y.col(i) = i;
}
else {
y.col(i) = i - cols;
}
}
}
// fft变换后进行频谱搬移
void fftshift(cv::Mat &plane0, cv::Mat &plane1)
{
// 以下的操作是移动图像 (零频移到中心)
int cx = plane0.cols / 2;
int cy = plane0.rows / 2;
cv::Mat part1_r(plane0, cv::Rect(0, 0, cx, cy)); // 元素坐标表示为(cx, cy)
cv::Mat part2_r(plane0, cv::Rect(cx, 0, cx, cy));
cv::Mat part3_r(plane0, cv::Rect(0, cy, cx, cy));
cv::Mat part4_r(plane0, cv::Rect(cx, cy, cx, cy));
cv::Mat temp;
part1_r.copyTo(temp); //左上与右下交换位置(实部)
part4_r.copyTo(part1_r);
temp.copyTo(part4_r);
part2_r.copyTo(temp); //右上与左下交换位置(实部)
part3_r.copyTo(part2_r);
temp.copyTo(part3_r);
cv::Mat part1_i(plane1, cv::Rect(0, 0, cx, cy)); //元素坐标(cx,cy)
cv::Mat part2_i(plane1, cv::Rect(cx, 0, cx, cy));
cv::Mat part3_i(plane1, cv::Rect(0, cy, cx, cy));
cv::Mat part4_i(plane1, cv::Rect(cx, cy, cx, cy));
part1_i.copyTo(temp); //左上与右下交换位置(虚部)
part4_i.copyTo(part1_i);
temp.copyTo(part4_i);
part2_i.copyTo(temp); //右上与左下交换位置(虚部)
part3_i.copyTo(part2_i);
temp.copyTo(part3_i);
}
Mat powZ(cv::InputArray src, double power) {
cv::Mat dst;
cv::pow(src, power, dst);
return dst;
}
Mat sqrtZ(cv::InputArray src) {
cv::Mat dst;
cv::sqrt(src, dst);
return dst;
}
测试效果
不同的滤波参数导致的滤波器尺寸大小不一,得到的结果也就不一样~
另外,如果我的代码有什么问题,欢迎大家提出异议批评指正,一同进步~
如果文章帮助到你了,可以点个赞让我知道,我会很快乐~加油!
文章出处登录后可见!