TLE两行根数简介及获取方法

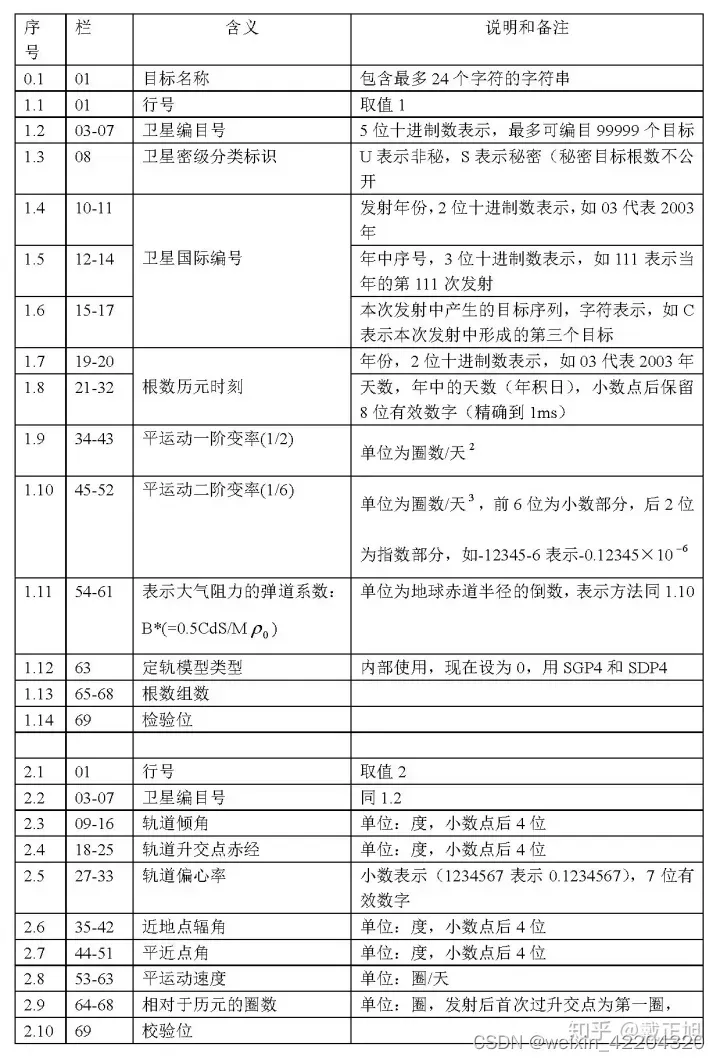
1、双行根数简介

美国是空间监测网最完善的国家，其SSN监测系统通过全球16个地方的31台雷达或望远镜可以跟踪直径大于10cｍ的空间物体，其控制中心对监测到的空间目标进行编目，并以双行轨道根数（TLE）形成空间目标数据库。NASA会定期公布空间目标的双行轨道根数形式的编目数据库，并公布了SGP4算法，但是TLE生成算法仍被保留。

空间目标的在轨摄动比较复杂，最主要的是地球非球形项摄动。若要提高定轨精度还需考虑其他较主要的摄动，如低轨目标要考虑大气摄动，高轨目标要考虑日月引力摄动，这会增加空间目标状态微分方程的复杂度，给微分方程离散线性化和非线性数值积分带来不便。Kozai基于非线性动力学中渐近平均法，提出针对轨道摄动中主要带谐项摄动的平均根数法，构造相应摄动方程的幂级数解；Brouwer利用Von-Zeipel正则变换方法给出了相应摄动方程的摄动解。根据上述方法，NORAD提出基于开普勒轨道根数的TLE以及相应的SGP轨道计算和预报算法。TLE主要参数项包括平均角速度，偏心率，轨道倾角，近地点辐角，升交点赤经，平近点角，平均角速度的一阶导数和归一化大气阻尼调制系数。TLE是包含了主要摄动项的平均轨道根数，采用类似平均根数法消除周期扰动项。由于算法特殊，必须用同样方法重构周期扰动项，才能得到较为精确的轨道数据，即只有利用NORAD发布的SGP模型才能保证轨道计算与预报精度。

1）双行根数格式

0 VANGUARD 3
1    20U 59007A   19299.40735246  .00000052  00000-0  27350-4 0  9992
2    20  33.3434 299.3949 1666264  99.9092 279.2854 11.55689740203444

2）双行根数下载

CelesTrak: Current GP Element Sets

2、SGP4算法

简化摄动模型（Simplified perturbations models）是用来计算航天器和空间碎片相对地心惯性坐标系运动状态向量的一组（五个）数学模型（SGP, SGP4, SDP4, SGP8 and SDP8）。这组模型被总称为SGP4，原因是经常用它处理NORAD和NASA的两行轨道根数。 这组模型考虑地球形状、大气阻力、光压、太阳和月亮的重力影响，计算其引起的摄动。

SGP可用于计算轨道周期小于225分钟的近地轨道物体的轨道。它对应轨道高度5877.5km的圆轨道。 SGP4和SDP4在1988年以fortran iv程序发布，对初始模型进行了改进，从而可以处理大量的轨道物体。SGP8和SDP8进一步改进了轨道衰变的模型。 SGP4模型在epoch误差为1km左右，每天的误差1-3km。因此nasa和norad频繁更新其轨道数据。

最早的sgp模型是1959年kozai提出的，1966年hilton和kuhlman改进，被用于美国空间监视控制中心监视轨道物体。SDP4模型在epoch误差为10km。 SDP4和SDP8是深空模型，仅使用简化阻力方程。因为对于阻力很大的卫星，不会在深空停留时间过长，它的轨道会快速下降，因此其误差影响不大。SDP4考虑了月球-太阳的重力摄动，对于24小时地球静止轨道和12小时闪电轨道还考虑了地球谐振项。 模型还有进一步修订，gsfc用来对seawifs任务进行跟踪，jpl用来对深空任务的数据通信给予支持。目前的代码库将SGP4和SDP4合并成了单一的库，统称为sgp4。

3、由瞬时密切轨道根数转TLE

若非必要，不建议做此转换。

适用TLE的坐标系为真赤道平春分点坐标系（TEME，True Equator Mean Equinox），其ｘ轴指向平春分点，ｚ轴与地球瞬时自转轴平行。而人卫工作中通常采用历元平赤道平春分点地心坐标系（MEME，Mean Equator Mean Equinox），如J2000地心赤道坐标系。

1）双行根数生成算法

空间目标TLE生成方法分为单点拟合和区间采样拟合：单点拟合的计算量相对较小，求解速度快，但是无法估计出大气阻力系数B*，拟合误差和轨道预报误差相对较大；区间采样拟合方法计算量大，但是拟合误差小，且预报精度较高，可以用于TLE发布。

2）基于STK的操作

STK中提供了Generate TLE的功能

打开Generate TLE功能界面，可见生成方法也分为区间拟合和单点拟合两种。Drag选项为是否估计B*参数，当选择方法为单点拟合（Single Point）时，B*参数估计不可用。从界面设置可以看出，影响生成TLE根数的主要因素有：①拟合方法；②参与拟合的数据段落；③迭代收敛条件。

Reports区域可以查看生成的结果（单点转换结果B*是为0）。

3）Connect命令

GenerateTLE<SatObjectPath> {Method} [{TimeInterval} <TimeStep>] “<TLEEpoch>” <SSCNumber> <MaxIterations> <Convergence> [{Routine}] [<NameOfNewSatellite>] [IntlDes <IntlDesignator>] [ElemNum <ElementNumber>] [BStar <BStarValue>] [Classification <Class>] [RevNumber <Value>]

从STK帮助文件中可以看到，GenerateTLE命令参数包括：拟合方法、采样区间时间、TLE历元时间、迭代收敛判据、是否估计B*参数等命令，典型语句：

GenerateTLE */Satellite/ERS1 Sampling "1 Jun 2004 12:00:00.00" "1 Jun 2004 20:00:00.00" 60.0 "1 Jun 2004 12:00:00.00" 55443 21 0.0003 SGP4 NewSat1
GenerateTLE */Satellite/Satellite1 Point "1 Jun 2004 12:00:00.00" 27556 20 0.0004

以上分别为区间拟合和单点拟合命令。

下面给出一段示例代码

% 创建卫星
strProSat = 'mySat';
fprintf('Create a new satellite %s\n',char(strProSat));

tmpSat = root.CurrentScenario.Children.New('eSatellite',char(strProSat));
tmpSat.SetPropagatorType('ePropagatorHPOP');
propagator = tmpSat.Propagator;
propagator.InitialState.Representation.AssignClassical('eCoordinateSystemJ2000',da,de,di,dw,dOm,dM);
propagator.InitialState.Representation.Epoch = strEpochTime;
propagator.Propagate;

%两行轨道根数，需要卫星编号，这里假设初始编号60000
ssc = 99999;
strcmd = ['GenerateTLE ','*/Satellite/mySat',' Sampling "',strBegTime,'" "',strEndTime,'" 30.0 "', strEpochTime,'" ', sprintf('%05.0f',ssc) , ' 20 0.001 SGP4 ', ' ','mySat_TLE'];
root.ExecuteCommand(strcmd);
satDP = tmpSat.DataProviders.Item('TLE Summary Data').Exec();
TLEData = satDP.DataSets.GetDataSetByName('TLE').GetValues;