文章目录
- 📝快速排序
-
- 🌠霍尔法
- 🌉三指针法
- 🌠挖坑法
-
- ✏️优化快速排序
- 🌠随机选key
-
- 🌉三位数取中
- 🌠小区间选择走插入,可以减少90%左右的递归
- 🌉 快速排序改非递归版本
- 🚩总结
📝快速排序
快速排序是一种分治算法。它通过一趟排序将数据分割成独立的两部分,然后再分别对这两部分数据进行快速排序。
本文将用3种方法实现:
🌠霍尔法
霍尔法是一种快速排序中常用的单趟排序方法,由霍尔先发现。
它通过选定一个基准数key(通常是第一个元素),然后利用双指针left和right的方式进行排序,right指针先找比key基准值小的数,left然后找比key基准值大的数,找到后将两个数交换位置,同时实现大数右移和小数左移,当left与right相遇就排序完成,然后将下标key的值与left交换,返回基准数key的下标,完成了单趟排序。这一过程使得基准数左侧的元素都比基准数小,右侧的元素都比基准数大。
如图动图展示:
以下是单趟排序的详解图解过程:
begin和end记录区间的范围,left记录做下标,从左向右遍历,right记录右下标,从右向左遍历,以第一个数key作为基基准值
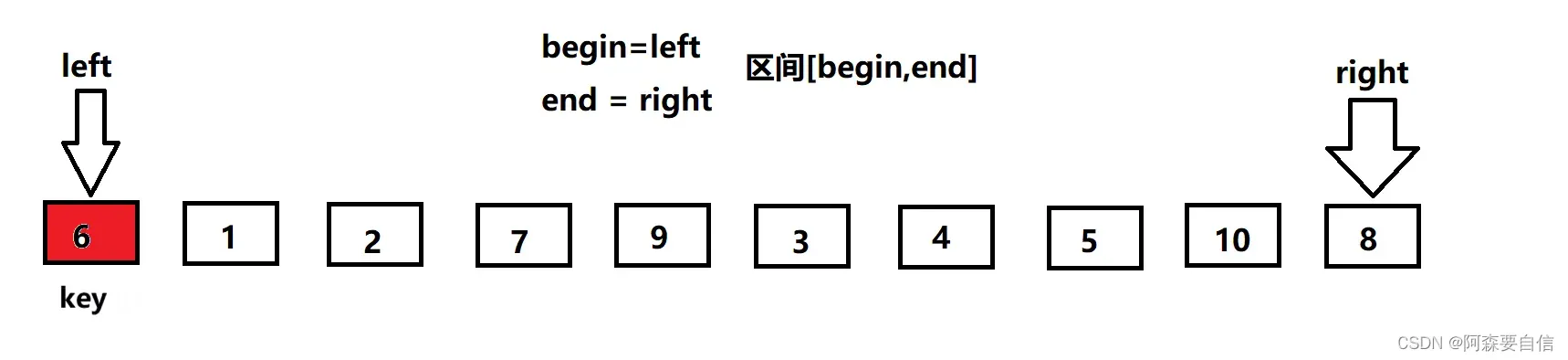
- 先让
right出发,找比key值小的值,找到就停下来
- 然后
left再出发,找比key大的值,若是找到则停下来,与right的值进行交换
- 接着
right继续找key小的值,找到后才让left找比key大的值,直到left相遇right,此时left会指向同一个数
- 将
left与right指向的数与key进行交换,单趟排序就完成了,最后将基准值的下标返回
为啥相遇位置比key要小->右边先走保证的
L遇R:R先走,R在比key小的位置停下来了,L没有找到比key大的,就会跟R相遇相遇位置R停下的位置,是比key小的位置R遇L:第一轮以后的,先交换了,L位置的值小于key,R位置的值大于key,R启动找小,没有找到,跟L相遇了,相遇位置L停下位置,这个位置比key小
- 第一轮
R遇L,那么就是R没有找到小的,直接就一路左移,遇到L,也就是key的位置
代码实现
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
//Hoare经典随机快排
void QuickSort1(int* a, int left, int right)
{
// 如果左指针大于等于右指针,表示数组为空或只有一个元素,直接返回
if (left >= right)
return;
// 区间只有一个值或者不存在就是最小子问题
int begin = left, end = right;// begin和end记录原始整个区间
// keyi为基准值下标,初始化为左指针
int keyi = left;
// 循环从left到right
while (left < right)
{
// right先走,找小,这里和下面的left<right一方面也是为了防止,right一路走出区间,走到left-1越界
while (left<right && a[right] >= a[keyi])
{
--right;
}
// 左指针移动,找比基准值大的元素
while (left<right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
// 交换左右指针所指元素
Swap(&a[left], &a[keyi]);
// 更新基准值下标
keyi = left;
// 递归排序左右两部分
//[begin , keyi-1]keyi[keyi+1 , end]
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
🌉三指针法
定义一个数组,第一个元素还是key基准值,定义前指针prev指向第一个数,后指针cur指向第二个数,让cur走,然后遍历数组,cur找到大于等于key基准值的数,cur++让cur向前走一步。当cur指针小于key基准值时,后指针加一走一步(++prev),然后交换prev和cur所指的值进行交换,因为这样cur一直都是小于key的值,让他继续向前不断找大的,而prev一直在找小的。依次类推,到cur遍历完数组,完成单趟排序。
如此动图理解:
简单总结:
以下是单趟排序的详解图解过程:
-
一开始,让
prev指向第一个数,cur指向prev的下一位,此时cur位置的数比key基准值小,所以prev加一后,与cur位置的数交换,由于此时prev+1 == cur,自己跟自己交换,交换没变,完了让cur++走下一个位置。
紧接着:
-
cur继续前进,此时来到了7的位置,大于key的值6,cur++继续向前走,来到9位置,9还是大于6,OK ! 我cur再cur++,来到3的位置,也是看到cur与prev拉开了距离,所以他又叫前后指针,这就体现出来,往下看–》
-
此时此刻,我
cur的值小于key基准值,先让prev走一步,然后与cur的值交换交换
-
同样的步骤,重复上述遍历,直到遍历完数组
cur遍历完数组后,将交换prev的值key的基准值进行交换,交换完,将key的下标更新为prev下标的,然后返回key下标,完成单趟。
代码如下:
void QuickSort2(int* a, int left, int right)
{
// 如果左指针大于等于右指针,表示数组为空或只有一个元素,直接返回
if (left >= right)
return;
// keyi为基准值下标,初始化为左指针
int keyi = left;
// prev记录每次交换后的下标
int prev = left;
// cur为遍历指针
int cur = left+1;
// 循环从左指针+1的位置开始到右指针结束
while (cur <= right)
{
// 如果cur位置元素小于基准值,并且prev不等于cur
// 就将prev和cur位置元素交换
// 并将prev后移一位
if (a[cur] < a[keyi] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;//不管是cur小于还是大于,是否交换,cur都后移一位 cur都++
}
// 将基准值和prev位置元素交换
Swap(&a[keyi], &a[prev]);
// 更新基准值下标为prev
keyi = prev;
// 递归调用左右两部分
// [left, keyi-1]keyi[keyi+1, right]
QuickSort2(a, left, keyi - 1);
QuickSort2(a, keyi + 1, right);
}
🌠挖坑法
挖坑法也是快速排序的一种单趟排序方法。它也是利用双指针,但与霍尔法不同的是,挖坑法在每次找到比基准数小的元素时,会将其值填入基准数所在的位置,然后将基准数所在的位置作为“坑”,接着从右边开始找比基准数大的元素填入这个“坑”,如此往复,直到双指针相遇。最后,将基准数填入最后一个“坑”的位置。
挖坑法思路:
您提到的挖坑法是一种快速排序的实现方式。
- 选择基准值(
key),将其值保存到另一个变量pivot中作为”坑” - 从左往右扫描,找到小于基准值的元素,将其值填入”坑”中,然后”坑”向右移动一个位置
- 从右往左扫描,找到大于或等于基准值的元素,将其值填入移动后的”坑”中
- 重复步骤
2和3,直到左右两个指针相遇 - 将基准值填入最后一个”坑”位置
- 对基准值左右两边递归分治,【
begin,key-1】key【key+1,end】重复上述过程,实现递归排序
与双指针法相比,挖坑法在处理基准值时使用了额外的”坑”变量,简化了元素交换的操作,但思想都是利用基准值将数组分割成两部分。
代码如下:
//挖坑法
void Dig_QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
//一趟的实现
int key = a[begin];
int pivot = begin;
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[pivot] = a[right];
pivot = right;
while (left < right && a[left] <= key)
{
left++;
}
a[pivot] = a[left];
pivot = left;
}
//补坑位
a[pivot] = key;
//递归分治
//[begin, piti - 1] piti [piti + 1, end]
Dig_QuickSort(a, begin, pivot - 1);
Dig_QuickSort(a, pivot + 1, end);
}
当你讨厌挖左边的坑,可以试试右边的坑😉:
代码如下:
// 交换元素
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
// 分区操作函数
int partition(int arr[], int low, int high)
{
// 取最后一个元素作为基准值
int pivot = arr[high];
// 初始化左右索引
int i = (low - 1);
// 从左到右遍历数组
for (int j = low; j <= high - 1; j++)
{
// 如果当前元素小于或等于基准值
if (arr[j] <= pivot)
{
// 左索引向右移动一位
i++;
// 将当前元素与左索引位置元素交换
swap(&arr[i], &arr[j]);
}
}
// 将基准值和左索引位置元素交换
swap(&arr[i + 1], &arr[high]);
// 返回基准值的最终位置
return (i + 1);
}
// 快速排序主函数
void quickSort(int arr[], int low, int high)
{
// 如果低位索引小于高位索引,表示需要继续排序
if (low < high)
{
// 调用分区函数,得到基准值的位置
int pi = partition(arr, low, high);
// 对基准值左边子数组递归调用快速排序
quickSort(arr, low, pi - 1);
// 对基准值右边子数组递归调用快速排序
quickSort(arr, pi + 1, high);
}
}
// 测试
int main()
{
// 测试数据
int arr1[] = { 5,3,6,2,10,1,4 };
int n1 = sizeof(arr1) / sizeof(arr1[0]);
quickSort(arr1, 0, n1 - 1);
// 输出排序结果
for (int i = 0; i < n1; i++)
{
printf("%d ", arr1[i]);
}
printf("\n");
int arr2[] = { 5,3,6,2,10,1,4,29,44,1,3,4,5,6 };
int n2 = sizeof(arr2) / sizeof(arr2[0]);
quickSort(arr2, 0, n2 - 1);
// 输出排序结果
for (int i = 0; i < n2; i++)
{
printf("%d ", arr2[i]);
}
printf("\n");
// 测试数据
int arr3[] = { 10,1,4,5,3,6,2,1 };
int n3 = sizeof(arr3) / sizeof(arr3[0]);
quickSort(arr3, 0, n3 - 1);
// 输出排序结果
for (int i = 0; i < n3; i++)
{
printf("%d ", arr3[i]);
}
printf("\n");
return 0;
}
运行启动:
✏️优化快速排序
🌠随机选key
为什么要使用随机数选取
key?
避免最坏情况,即每次选择子数组第一个或最后一个元素作为key,这样会导致时间复杂度退化为O(n^2)。
随机化可以减少排序不均匀数据对算法性能的影响。
相比固定选择第一个或最后一个元素,随机选择key可以在概率上提高算法的平均性能。
这里是优化快速排序使用随机数选取key的方法:
- 在划分子数组前,随机生成一个
[left,right]区间中的随机数randi, - 将随机
randi处的元素与区间起始元素left交换 - 使用这个随机索引取出子数组中的元素作为keyi。
随机选key逻辑代码:
//快排,随机选key
void QuickSort3(int* a, int left, int right)
{
//区间只有一个值或者不存在就是最小子问题
if (left >= right)
return;
int begin = left, end = right;
//选[left,right]区间中的随机数做key
int randi = rand() % (right - left + 1);
//rand() % N生成0到N-1的随机数
randi += left;
//将随机索引处的元素与区间起始元素交换
Swap(&a[left], &a[randi]);
//用交换后的元素作为基准值keyi
int keyi = left;
while (left < right)
{
//从右向左找小于key的元素
while (left < right && a[right] >= a[keyi])
{
--right;
}
//从左向右找大于key的元素
while (left < right && a[left] <= a[keyi])
{
++left;
}
//交换元素
Swap(&a[left], &a[right]);
}
//将基准值与交叉点元素交换
Swap(&a[left], &a[keyi]);
keyi = left;
//递归处理子区间
QuickSort3(a, begin, keyi - 1);
QuickSort3(a, keyi + 1, end);
}
🌉三位数取中
有无序数列数组的首和尾后,我们只需要在首,中,尾这三个数据中,选择一个排在中间的数据作为基准值(keyi),进行快速排序,减少极端情况,进一步提高快速排序的平均性能。
代码实现:
// 三数取中 left mid right
// 大小居中的值,也就是不是最大也不是最小的
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
取中的返回函数接收:
int begin = left, end = right;
// 三数取中
int midi = GetMidi(a, left, right);
//printf("%d\n", midi);
Swap(&a[left], &a[midi]);
整体函数实现:
//三数取中 left mid right
//大小居中的值,也就是不是最大,也不是最小的
int GetMid(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if(a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else//a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[right] > a[left])
{
return left;
}
else
{
return right;
}
}
}
void QuickSort4(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left, end = right;
//三数取中
int midi = GetMid(a, left, right);
//printf("%d\n",midi);
Swap(&a[left], &a[midi]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
--right;
}
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
QuickSort4(a, begin, keyi - 1);
QuickSort4(a, keyi + 1, end);
}
🌠小区间选择走插入,可以减少90%左右的递归
对于小区间,使用插入排序而不是递归进行快速排序。
在快速排序递归中,检查子问题的区间长度是否小于某个阈值(如10-20),如果区间长度小于阈值,则使用插入排序进行排序,否则使用快速排序递归进行划分。
而这个(如10-20)刚好可以在递归二叉树中体现出来。
如图:
当然从向下建堆优于向上建堆,也可以体现出来:
优点在于:对于小区间,插入排序效率高于快速排序的递归开销大部分数组元素位于小区间中,采用插入排序可以省去90%左右的递归调用,但整体数组规模大时,主要工作还是由快速排序完成
与三数取中进行合用
void QuickSort5(int* a, int left, int right)
{
if (left >= right)
return;
// 小区间选择走插入,可以减少90%左右的递归
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);
}
else
{
int begin = left, end = right;
//三数取中
int midi = GetMid(a, left, right);
//printf("%d\n",midi);
Swap(&a[left], &a[midi]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
--right;
}
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
QuickSort4(a, begin, keyi - 1);
QuickSort4(a, keyi + 1, end);
}
}
🌉 快速排序改非递归版本
逻辑原理:
非递归版本的快速排序利用了栈来模拟递归的过程。它的基本思想是:将待排序数组的起始和结束位置压入栈中,然后不断出栈,进行单趟排序,直到栈为空为止。在单趟排序中,选取基准数,将小于基准数的元素移到基准数左边,大于基准数的元素移到基准数右边,并返回基准数的位置。然后根据基准数的位置,将分区的起始和结束位置入栈,继续下一轮排序,直到所有子数组有序。
代码实现步骤:
- 初始化一个栈用于保存待排序子数组的起始和结束位置。
- 将整个数组的起始和结束位置压入栈中。
- 循环执行以下步骤,直到栈为空:
出栈,获取当前待排序子数组的起始和结束位置。
进行单趟排序,选取基准数,并将小于基准数的元素移到左边,大于基准数的元素移到右边。
根据基准数的位置,将分区的起始和结束位置入栈。 - 排序结束。
代码实现
#include "Stack.h"
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
//单趟
int keyi = begin;
int prev = begin;
int cur = begin + 1;
while (cur <= end)
{
if (a[cur] < a[keyi] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
//[begin,keyi-1]keyi[keyi+1,end]
if (keyi + 1 < end)
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (keyi - 1 > begin)
{
STPush(&st, keyi - 1);
STPush(&st, begin);
}
}
STDestroy(&st);
}
以下是栈的实现:
Stack.c
#include"Stack.h"
void STInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}
void STDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
// 栈顶
// 11:55
void STPush(ST* ps, STDataType x)
{
assert(ps);
// 满了, 扩容
if (ps->top == ps->capacity)
{
int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* tmp = (STDataType*)realloc(ps->a, newcapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
ps->a = tmp;
ps->capacity = newcapacity;
}
ps->a[ps->top] = x;
ps->top++;
}
void STPop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));
ps->top--;
}
STDataType STTop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));
return ps->a[ps->top - 1];
}
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
栈的头文件实现:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
void STInit(ST* ps);
void STDestroy(ST* ps);
// 栈顶
void STPush(ST* ps, STDataType x);
void STPop(ST* ps);
STDataType STTop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);
🚩总结
快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
因此
时间复杂度:O(N*logN)
什么情况快排最坏:有序/接近有序 ->O(N^2)
但是如果加上随机选key或者三数取中选key,最坏情况不会出现,所以这里不看最坏
快排可以很快,你的点赞也可以很快,哈哈哈,感谢💓 💗 💕 💞,喜欢的话可以点个关注,也可以给博主点一个小小的赞😘呀
版权声明:本文为博主作者:阿森要自信原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/a_hong_sen/article/details/136967292