四叉树编码
1.四叉树编码定义
四叉树数据结构是一种对栅格数据的压缩编码方法,其基本思想是将一幅栅格数据层或图像等分为四部分,逐块检查其格网属性值(或灰度);如果某个子区的所有格网值都具有相同的值,则这个子区就不再分割,否则还要把这个子区再分割成四个子区,这样依次地分割,直到每个子块都只含有相同的属性值或灰度值为止,可分为自上而下编码和自下而上编码
2.四叉树表示形式
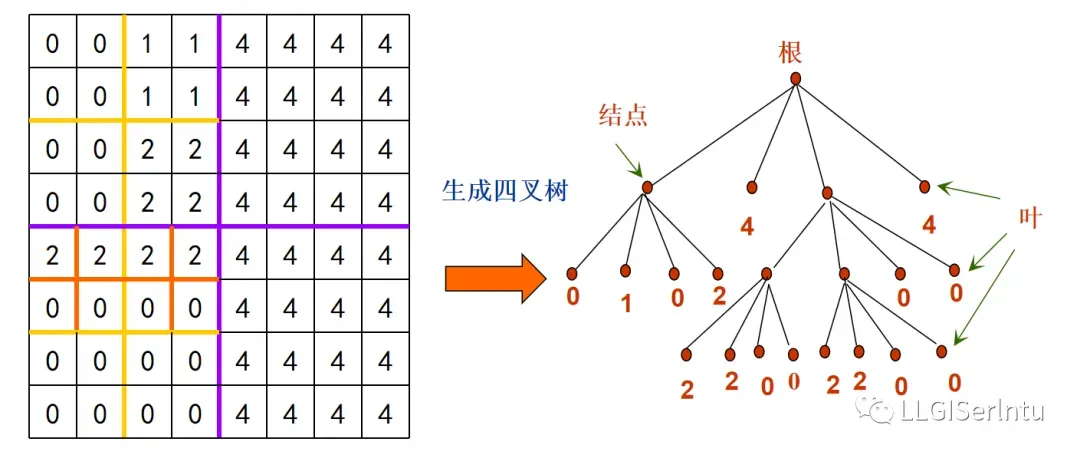
用一倒立树表示这种分割和分割结果,如图所示。
根:整个区域
高:深度、分几级,几次分割
叶:不能再分割的块
结点(或树叉):还需分割的块
每个树叉均有4个分叉,叫四叉树。
3.四叉树的分类
四叉树分为常规四叉树和线性四叉树
(1) 常规四叉树(记录这棵树的叶结点外,中间结点,结点之间的联系用指针联系,每个结点需要6个变量:父结点指针、四个子结点的指针和本结点的属性值。)
指针不仅增加了数据的存储量,还增加了操作的复杂性:如层次数(分割次数)由从父结点移到根结点的次数来确定,结点所代表的图像块的位置需要从根节点开始逐步推算下来。所以,常规四叉树并不广泛用于存储数据,主要在数据索引和图幅索引等方面应用
(2)线性四叉树则只存贮最后叶结点的信息,包括叶结点的位置编码/地址码、属性或灰度值;线性四叉树地址码,通常采用十进制Morton码(MD码):如图所示
①下图为一个8*8原始栅格数据
②依据自下而上的编码方式进行莫顿码编码
③在存储时,只存储属性值发生改变位置的莫顿码,就是叶节点的属性值
④如何计算莫顿码:如图所示,通常是将栅格数据十进制的行列号,转成二进制的行列号,再将二进制的行号和列号进行错位交叉排列,得到二进制的莫顿码,再将二进制的莫顿码转成十进制的莫顿码
4.四叉树编码特征
优点:
1)存贮量小,只对叶结点编码,节省了大量中间结点的存储,地址码隐含着结点的分割路径和分割次数。对于团块图像,四叉树表示法占用空间比上述其他方法要少得多,四叉树表示法基本上是一种非冗余表示法。
2)线性四叉树可直接寻址,通过其坐标值直接计算其Morton码,而不用建立四叉树(自下而上)。
3) 容易执行实现集合相加等组合操作
4)四叉树具有可变率或多重分辩率的特点使得它有很好的应用前景,适用于处理凝聚性或呈块状分布的空间数据,特别适用于处理分布不均匀的块状空间数据,但不适用于连续表面(如地形)或线状地物。
缺点
1)四叉树未能直接表示物体间的拓扑关系。
2) 与非树表示法比较,四叉树表示法的缺点在于转换的不稳定性或叫滑动变异
例如,两个图像的差异仅由于平移,就会构成极为不同的四叉树,因而很难根据四叉树来判断这两个图像是否全同,故不利于做形状分析和模式识别,
3) 一个物体的图像在构成四叉树时会被分割到若干个象限中,使它失去了内在的相关性。
4)矢/栅正反变换还不理想。
5) 建立四叉树耗费机时很多。
6) 四叉树虽可修改,但很费事
版权声明:本文为博主作者:lntu_ling原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/lling0309/article/details/134216430