一. SGD,Adam,AdamW,LAMB优化器
优化器是用来更新和计算影响模型训练和模型输出的网络参数,使其逼近或达到最优值,从而最小化(或最大化)损失函数。
1. SGD
随机梯度下降是最简单的优化器,它采用了简单的梯度下降法,只更新每一步的梯度,但是它的收敛速度会受到学习率的影响。
优点: 简单性,在优化算法中没有太多的参数需要调整,通过少量的计算量就可以获得比较好的结果。
缺点: 在某些极端情况下容易受到局部最小值的影响,也容易出现收敛的问题。
1. Adam
为解决 GD 中固定学习率带来的不同参数间收敛速度不一致的弊端,AdaGrad 和 RMSprop 诞生出来,为每个参数赋予独立的学习率。计算梯度后,梯度较大的参数获得的学习率较低,反之亦然。此外,为避免每次梯度更新时都独立计算梯度,导致梯度方向持续变化,Momentum 将上一轮梯度值加入到当前梯度的计算中,通过某种权重对两者加权求和,获得当前批次参数更新的梯度值。 Adam 结合了这两项考虑,既为每一个浮点参数自适应性地设置学习率,又将过去的梯度历史纳入考量,其实现原理如下:
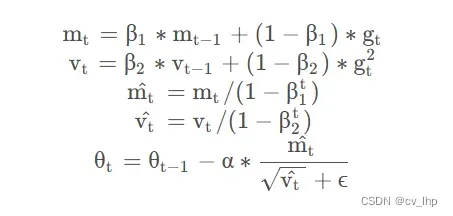
计算一阶、二阶动量矩,加入偏置修正,最后更新参数,gt表示t时刻梯度。从上述公式可以看出,训练前期的学习率和梯度更新是比较激进的,到后期逐渐平稳。虽然 Adam 优化器的使用会导致内存中多出两倍于原参数体量的占用,但与之换来的训练收益使得学术界并没有放弃这一高效的方法。
代码实现比较简单,照着公式敲就行了:
import autograd.numpy as np
from autograd import grad
class Adam:
def __init__(self, loss, weights, lr=0.001, beta1=0.9, beta2=0.999, epislon=1e-8):
self.loss = loss
self.theta = weights
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.epislon = epislon
self.get_gradient = grad(loss)
self.m = 0
self.v = 0
self.t = 0
def minimize_raw(self):
self.t += 1
g = self.get_gradient(self.loss)
self.m = self.beta1 * self.m + (1 - self.beta1) * g
self.v = self.beta2 * self.v + (1 - self.beta2) * (g * g)
self.m_hat = self.m / (1 - self.beta1 ** self.t)
self.v_hat = self.v / (1 - self.beta2 ** self.t)
self.theta = self.theta - self.lr * self.m_hat / (self.v_hat ** 0.5 + self.epislon)
2. AdamW
Adam 虽然收敛速度快,但没能解决参数过拟合的问题。学术界讨论了诸多方案,其中包括在损失函数中引入参数的 L2 正则项。这样的方法在其他的优化器中或许有效,但会因为 Adam 中自适应学习率的存在而对使用 Adam 优化器的模型失效,具体分析可见fastai的这篇文章:AdamW and Super-convergence is now the fastest way to train neural nets。AdamW 的出现便是为了解决这一问题,达到同样使参数接近于 0 的目的。具体的举措,是在最终的参数更新时引入参数自身:
λ 即为权重衰减因子,常见的设置为 0.005/0.01。这一优化策略目前正广泛应用于各大预训练语言模型。
代码实现:
class AdamW:
def __init__(self, loss, weights, lambda1, lr=0.001, beta1=0.9, beta2=0.999, epislon=1e-8):
self.loss = loss
self.theta = weights
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.epislon = epislon
self.lambda1 = lambda1
self.get_gradient = grad(loss)
self.m = 0
self.v = 0
self.t = 0
def minimize_raw(self):
self.t += 1
g = self.get_gradient(self.loss)
self.m = self.beta1 * self.m + (1 - self.beta1) * g
self.v = self.beta2 * self.v + (1 - self.beta2) * (g * g)
self.m_hat = self.m / (1 - self.beta1 ** self.t)
self.v_hat = self.v / (1 - self.beta2 ** self.t)
self.theta = self.theta - self.lr * (
self.m_hat / (self.v_hat ** 0.5 + self.epislon) + self.lambda1 * self.theta)
3. LAMB
LAMB 优化器是 2019 年出现的一匹新秀,它将bert模型的预训练时间从3天压缩到了76分钟! LAMB 出现的目的是加速预训练进程,这个优化器也成为 NLP 社区为泛机器学习领域做出的一大贡献。在使用 Adam 和 AdamW 等优化器时,一大问题在于 batch size 存在一定的隐式上限,一旦突破这个上限,梯度更新极端的取值会导致自适应学习率调整后极为困难的收敛,从而无法享受增加的 batch size 带来的提速增益。LAMB 优化器的作用便在于使模型在进行大批量数据训练时,能够维持梯度更新的精度。具体来说,LAMB 优化器支持自适应元素级更新(adaptive element-wise updating)和准确的逐层修正(layer-wise correction)。LAMB 可将 BERT 预训练的批量大小扩展到 64K,且不会造成准确率损失。BERT 预训练包括两个阶段:1)前 9/10 的训练 epoch 使用 128 的序列长度,2)最后 1/10 的训练 epoch 使用 512 的序列长度。LAMB的算法如下:
其中,
以下是 LAMB 优化器的 tensorflow1.x 代码,可作为参考以理解算法:
class LAMBOptimizer(tf.train.Optimizer):
'''
LAMBOptimizer optimizer.
# Important Note
- This is NOT an official implementation.
- LAMB optimizer is changed from arXiv v1 ~ v3.
- We implement v3 version (which is the latest version on June, 2019.).
- Our implementation is based on `AdamWeightDecayOptimizer` in BERT (provided by Google).
# References
- LAMB optimier: https://github.com/ymcui/LAMB_Optimizer_TF
- Large Batch Optimization for Deep Learning: Training BERT in 76 minutes. https://arxiv.org/abs/1904.00962v3
- BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. https://arxiv.org/abs/1810.04805
# Parameters
- There is nothing special, just the same as `AdamWeightDecayOptimizer`.
'''
def __init__(self,
learning_rate,
weight_decay_rate=0.01,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-6,
exclude_from_weight_decay=None,
name="LAMBOptimizer"):
"""Constructs a LAMBOptimizer."""
super(LAMBOptimizer, self).__init__(False, name)
self.learning_rate = learning_rate
self.weight_decay_rate = weight_decay_rate
self.beta_1 = beta_1
self.beta_2 = beta_2
self.epsilon = epsilon
self.exclude_from_weight_decay = exclude_from_weight_decay
def apply_gradients(self, grads_and_vars, global_step=None, name=None):
"""See base class."""
assignments = []
for (grad, param) in grads_and_vars:
if grad is None or param is None:
continue
param_name = self._get_variable_name(param.name)
m = tf.get_variable(
name=param_name + "/lamb_m",
shape=param.shape.as_list(),
dtype=tf.float32,
trainable=False,
initializer=tf.zeros_initializer())
v = tf.get_variable(
name=param_name + "/lamb_v",
shape=param.shape.as_list(),
dtype=tf.float32,
trainable=False,
initializer=tf.zeros_initializer())
# Standard Adam update.
next_m = (
tf.multiply(self.beta_1, m) + tf.multiply(1.0 - self.beta_1, grad))
next_v = (
tf.multiply(self.beta_2, v) + tf.multiply(1.0 - self.beta_2,
tf.square(grad)))
update = next_m / (tf.sqrt(next_v) + self.epsilon)
# Just adding the square of the weights to the loss function is *not*
# the correct way of using L2 regularization/weight decay with Adam,
# since that will interact with the m and v parameters in strange ways.
#
# Instead we want ot decay the weights in a manner that doesn't interact
# with the m/v parameters. This is equivalent to adding the square
# of the weights to the loss with plain (non-momentum) SGD.
if self._do_use_weight_decay(param_name):
update += self.weight_decay_rate * param
############## BELOW ARE THE SPECIFIC PARTS FOR LAMB ##############
# Note: Here are two choices for scaling function \phi(z)
# minmax: \phi(z) = min(max(z, \gamma_l), \gamma_u)
# identity: \phi(z) = z
# The authors does not mention what is \gamma_l and \gamma_u
# UPDATE: after asking authors, they provide me the code below.
# ratio = array_ops.where(math_ops.greater(w_norm, 0), array_ops.where(
# math_ops.greater(g_norm, 0), (w_norm / g_norm), 1.0), 1.0)
r1 = tf.sqrt(tf.reduce_sum(tf.square(param)))
r2 = tf.sqrt(tf.reduce_sum(tf.square(update)))
r = tf.where(tf.greater(r1, 0.0),
tf.where(tf.greater(r2, 0.0),
r1 / r2,
1.0),
1.0)
eta = self.learning_rate * r
update_with_lr = eta * update
next_param = param - update_with_lr
assignments.extend(
[param.assign(next_param),
m.assign(next_m),
v.assign(next_v)])
return tf.group(*assignments, name=name)
def _do_use_weight_decay(self, param_name):
"""Whether to use L2 weight decay for `param_name`."""
if not self.weight_decay_rate:
return False
if self.exclude_from_weight_decay:
for r in self.exclude_from_weight_decay:
if re.search(r, param_name) is not None:
return False
return True
def _get_variable_name(self, param_name):
"""Get the variable name from the tensor name."""
m = re.match("^(.*):\\d+$", param_name)
if m is not None:
param_name = m.group(1)
return param_name
二. 参考链接
- Adam,AdamW,LAMB优化器原理与代码
- 优化器SGD、Adam和AdamW的区别和联系
文章出处登录后可见!