深度学习基础实例与总结

一、神经网络

1 深度学习

1 什么是深度学习？

简单来说，深度学习就是一种包括多个隐含层 (越多即为越深)的多层感知机。它通过组合低层特征，形成更为抽象的高层表示，用以描述被识别对象的高级属性类别或特征。 能自生成数据的中间表示(虽然这个表示并不能被人类理解)，是深度学习区别于其它机器学习算法的独门绝技。
所以，深度学习可以总结成: 通过加深网络，提取数据深层次特征。

2 深度学习与传统机器学习对比

1）相同点

目的相同：都是利用机器自我学习能力，解决软件系统的难题

基本问题相同：回归问题、分类问题、聚类问题

基本流程相同：模型构建数据准备–>模型选择 –>/训练–> 模型评估基本流程相同:–>预测

问题领域相同

• 样本是否有标签:监督学习、非监督学习、半监督学习
• 应用领域:推荐引擎、计算机视觉、自然语言处理、强化学习

评价标准相同

• 回归问题:均方误差;R2值
• 分类问题:交又熵;查准率、召回率、F1综合系数
• 模型泛化能力:过拟合、欠拟合

2）不同点

深度网络进化过程

3 感知机与神经网络

1）生物神经元

2）生物神经网络

3）什么是感知机

感知机(Perceptron)，又称神经元(Neuron，对生物神经元进行了模仿)是神经网络(深度学习)的起源管法，1958年由康奈尔大学心理学教授弗兰克·罗森布拉特(Frank Rosenblatt) 提出，它可以接收多个输入信号，产生一个输出信号。

其中，和称为输入，和为权重，为闯值，y为输出。

4）感知机的功能

• 作为分类器/回归器，实现自我学习
• 实现逻辑运算包括逻辑或(OR)，逻辑和 (AND)
• 组成神经网络

（1）实现逻辑和

（2）实现逻辑或

5) 感知机缺陷

感知机的局限在于无法处理“异或”问题(非线性问题)

6）多层感知机

1975年，感知机的“异或”难题才被理论界彻底解决，即通过多个感知机组合来解决该问题，这种模型也叫多层感知机(Multi-Layer Perceptron，MLP)。如下图所示，神经元节点闯值均设置为0.5。

7）神经网络

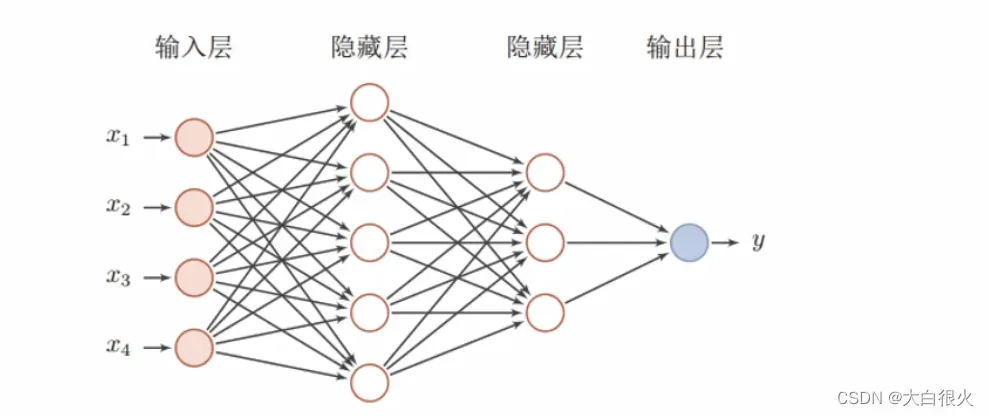
感知机由于结构简单，完成的功能十分有限。可以将若干个感知机连在一起，形成个级联网络结构，这个结构称为“多层前馈神经网络” (Multi-layerFeedforward NeuralNetworks)。所谓“前馈”是指将前一层的输出作为后层的输入的逻辑结构。每一层神经元仅与下一层的神经元全连接。但在同一层之内神经元彼此不连接，而且跨层之间的神经元，彼此也不相连。

8）神经网络的功能

1989年，奥地利学者库尔特·霍尼克 (Kurt Hornik) 等人发表论文证明，对于任意复杂度的连续波莱尔可测函数 (Borel Measurable Function) ，仅仅需要一个隐含层，只要这个隐含层包括足够多的神经元，前馈神经网络使用挤压函数 (Squashing Function) 作为激活函数，就可以以任意精度来近似模拟。如果想增加f的近似精度，单纯依靠增加神经元的数目即可实现。这个定理也被称为通用近似定理(Universal Approximation Theorem)该定理表明，前馈神经网在理论上可近似解决任何问题.

9) 深层网络优点

其实，神经网络的结构还有另外一个“进化”方向，那就是朝着“纵深”方向发展，也就是说，减少单层的神经元数量，而增加神经网络的层数，也就是“深”而“瘦”的网络模型。

微软研究院的科研人员就以上两类网络性能展开了实验，实验结果表明: 增加网络的层数会显著提升神经网络系统的学习性能。

10）激活函数

在神经网络中，将输入信号的总和转换为输出信号的函数被称为激活函数 (activation function)

为什么要使用激活函数？

激活函数将多层感知机输出转换为非线性，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

如果一个多层网络，使用连续函数作为激活函数的多层网络，称之为“神经网络”，否则称为“多层感知机”。所以，激活函数是区别多层感知机和神经网络的依据。

常见的激活函数

（1）sigmod函数

sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类，表达式: f(x) = 1/(1 +)

缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法，反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

（2）tanh双曲正切函数

优点:平滑、易于求导;输出均值为0，收敛速度要比sigmoid快，从而可以减少迭代次数
缺点:梯度消失
用途:常用于NLP中

（3）Relu（Rectified Linear Units，修正线性单元）

（4）Softplus

Softplus是对ReLU的平滑逼近解析形式，更巧的是，Softplus函数的导数恰好就是Sigmoid函数。但实际应用效果不如ReLU好

（5）Softmax

Softmax函数定义如下，其中Vi 是分类器前级输出单元的输出。i表示类别索引，总的类别个数为Csi表示的是当前元素的指数与所有元素指数和的比值。通过Softmax函数就可以将多分类的输出数值转化为相对概率，而这些值的累和为1，常用于神经网络输出层。表达式：

4 损失函数

1）什么是损失函数

损失函数(Loss Function)，也有称之为代价函数 (Cost Function)，用来度量预测值和实际值之间的差异。

2）损失函数的作用

度量决策函数和实际值之间的差异。

作为模型性能参考。损失函数值越小，说明预测输出和实际结果(也称期望输出)之间的差值就越小，也就说明我们构建的模型越好。

学习的过程，就是不断通过训练数据进行预测，不断调整预测输出与实际输出差异，使的损失值最小的过程。

3）常用损失函数

（1）均方误差（Mean Square error, MSE）损失函数

均方误差是回归问题常用的损失函数，它是预测值与目标值之间差值的平方和，其公式和图像如下所示：

为什么使用误差的平方？

• 曲线的最低点是可导的。

• 越接近最低点，曲线的坡度逐渐放缓，有助于通过当前的梯度来判断接近最低点的程度(是否逐渐减少步长，以免错过最低点)。

（2）交叉熵(Cross Entropy)。

交叉熵是Shannon信息论中一个重要概念主要用于度量两个概率分布间的差异性信息，在机器学习中用来作为分类问题的损失函数。假设有两个概率分布，与，其交叉函数公式及图形如下所示：

5 梯度下降算法

1）批量梯度下降

批量梯度下降法(Batch Gradient Descent，BGD)是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。

优点: 一定能得到最优
一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行
由全数据集确定的方向能够更好地代表样本总 体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优
缺点:速度太慢
当样本数目很大时，每选代一步都需要对所有样本计算，训练过程会很慢

2）随机梯度下降

随机梯度下降法(Stochastic Gradient Descent，SGD)每次选代使用一个样本来对参数进行更新，使得训练速度加快。

优点:
由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快
缺点:
准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
不易于并行实现。

3）小批量梯度下降（优先）

小批量梯度下降(Mini-Batch Gradient Descent，MBGD)是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是:每次选代使用指定个(batch size)样本来对参数进行更新

优点:
通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果
缺点:
batchsize的不当选择可能会带来一些问题

6 反向传播

1）什么是正向传播网络

前一层的输出作为后一层的输入的逻辑结构，每一层神经元仅与下一层的神经元全连接，通过增加神经网络的层数虽然可为其提供更大的灵活性让网络具有更强的表征能力，也就是说，能解决的问题更多，但随之而来的数量庞大的网络参数的训练，一直是制约多层神经网络发展的一个重要瓶颈。

2）什么是反向传播

反向传播 (Backpropagation algorithm)全称“误差反向传播是在深度神经网络中，根据输出层输出值，来反向调整隐藏层权重的一种方法。

3）为什么需要反向传播

为什么不直接使用梯度下降而使用反向传播方式更新权重呢?

梯度下降应用于有明确求导函数的情况，或者可以求出误差的情况(比如线性回归)，我们可以把它看做没有隐藏层的网络。但对于多个隐藏层的神经网络，输出层可以直接求出误差来更新参数，但隐藏层的误差是不存在的，因此不能对它直接应用梯度下降，而是先将误差反向传播至隐藏层然后再应用梯度下降。

4）反向传播算法极简史

1974年，哈佛大学沃伯斯博士在他的博士论文中，首次提出了 通过误差的反向传播来训练人工神经网络，以解决神经网络数量庞大的参数训练问题。 但是，沃伯斯的工作并没有得到足够的重视，因为当时神经网络正陷入低潮，可谓“生不逢时”。

1986年，由杰弗里·辛顿 (Geoffrey Hinton)和大卫·鲁姆哈特 (David Rumelhart)等人在著名学术期刊Nature(自然)上发表了论文“借助误差反向传播算法的学习表征(Learning Representations by Back-propagating errors)”，系统而简洁地阐述了反向传播算法在神经网络模型上的应用。反向传播算法非常好使，它直接把纠错的运算量降低到只和神经元数目本身成正比的程度。

后来，沃伯斯得到了IEEE(电气电子工程师学会)神经网络分会的先驱奖;Geoffrey Hinton与Yoshua Bengio、Yann LeCun (合称“深度学习三巨头”)共同获得了2018年的图灵奖

二、卷积神经网络

1. 卷积

1.1 特征图像宽和高的计算公式

1.2 三维的图像

1.3 多通道多卷积核的卷积

每个通道先与第一组卷积核执行卷积，然后多通道结果叠加，产生一个输出

每个通道与下一组卷积核执行卷积产生另一个输出

有多少组卷积核，就有多少个通道输出(如右图，两组卷积核，产生两个通道的输出数据)

1.4 scipy实现卷积实例

scipy版本为1.2.1

from scipy import signal
from scipy import misc
import numpy as np
import matplotlib.pyplot as plt

data = misc.imread('zebra.png', flatten=True)

kernel0 = np.array([[-1, 0, 1],
                    [-2, 0, 2],
                     [-1, 0, 1]])

kernel1 = np.array([[-1, -2, -1],
                    [0, 0, 0],
                    [1, 2, 1]])

conv0 = signal.convolve2d(data, kernel0, boundary='symm', mode='same').astype('int32')
conv1 = signal.convolve2d(data, kernel1, boundary='symm', mode='same').astype('int32')

plt.figure('convolutional 2D')

plt.subplot(1, 3, 1)
plt.imshow(data, cmap='gray')
plt.xticks([])
plt.yticks([])

plt.subplot(1, 3, 2)
plt.imshow(conv0, cmap='gray')
plt.xticks([])
plt.yticks([])

plt.subplot(1, 3, 3)
plt.imshow(conv1, cmap='gray')
plt.xticks([])
plt.yticks([])

plt.show()

2. 卷积神经网络结构

1）总结结构

通常情况下，卷积神经网络由若干个卷积层(Convolutional Layer)、激活层(Activation Layer)、池化层 (Pooling Layer) 及全连接层 (FullyConnected Layer)组成。

2）卷积层

它是卷积神经网络的核心所在，通过卷积运算，达到降维处理和提取特征两个重要目的。

3）激活层

其作用在于将前一层的线性输出，通过非线性的激活函数进行处理，这样用以模拟任意函数，从而增强网络的表征能力。前面章节中介绍的激活函数如挤压函数Sigmoid也是可用的，但效果并不好。在深度学习领域，ReLU(Rectified-Linear Unit，修正线性单元)是目前使用较多的激活函数，主要原因是它收敛更快，次要原因在于它部分解决了梯度消失问题。

4）池化层（Pooling Layer）

也称子采样层或下采样层(Subsampling Layer)，目的是缩小高、长方向上的空间的运算，以降低计算量，提高泛化能力。如下的示例，将44的矩阵缩小成22的矩阵输出。

池化层计算：
对于每个输入矩阵，我们将其切割成若千大小相等的正方形小块对每一个区块取最大值或者平均值，并将结果组成一个新的矩阵。

Max池化:对各个参与池化计算的区域取最大值，形成的新矩阵在图像识别领域，主要使用Max池化。
Average池化:对各个参与池化计算的区域计算平均值。

池化层特点：
没有要学习的参数。池化层和卷积层不同，没有要学习的参数。池化只是从目标区域中取最大值(或者平均值)，所以不存在要学习的参数；
通道数不发生变化。经过池化运算，输入数据和输出数据的通道数不会发生变化；
对微小的位置变化具有鲁棒性 (健壮)。输入数据发生微小偏差时，池化仍会返回相同的结果。

5）全连接层

这个网络层相当于多层感知机(Multi-Layer Perceptron，简称MLP)其在整个卷积神经网络中起到分类器的作用通过前面多个“卷积-激活-池化”层的反复处理，待处理的数据特性已有了显著提高:一方面，输入数据的维度已下降到可用传统的前馈全连接网络来处理了，另一方面此时的全连接层输入的数据已不再是“泥沙俱下、鱼龙混杂”，而是经过反复提纯过的结果，因此输出的分类品质要高得多

3 经典CNN介绍

1）LeNet

LeNet是 Yann LeCun在1998年提出，用于解决手写数字识别的视觉任务。自那时起，CNN的最基本的架构就定下来了: 卷积层、池化层、全连接层。

（1） 网络结构

（2）主要参数

• 输入32*32大小单通道图像输入
• 两个“卷积-池化层
• 第一个全连接层神经元数目为500，再接激活函数
• 第二个全连接层神经元数目为10，得到10维的特征向量，用于10个数字的分类训练，送入softmaxt分类，得到分类结果的概率

2）AlexNet

AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生Alex Krizhevsky设计的，把CNN的基本原理应用到了很深很宽的网络中。

（1）特点

• 使用ReLU作为激活函数，并验证其效果在较深的网络超过了Sigmoid，成功解决了Sigmoid在网络较深时的梯度弥散问题
• 使用Dropout(丢弃学习)随机忽略一部分神经元防止过拟合
• 在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化，AlexNet全部使用最大池化，避免平均池化的模糊化效果
• 提出了LRN (Local Response Normalization，局部正规化)层，对局部神经元的活动创建竞争机制使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力
• 使用CUDA加速深度卷积网络的训练，利用GPU强大的并行计算能力，处理神经网络训练时大量的矩阵运算

（2）网络结构

（3）主要参数

• AlexNet网络包含8层，其中前5层为卷积-池化层，后3层为全连接层;输入224x224x3的图像，
• 第一卷积层用96个11x11x3的卷积核对进行滤波，步幅4像素，全连接的每层有4096个神经元，
• 最后一个完全连接的层的输出被馈送到1000路SoftMax，它产生超过1000个类别标签的分布;整个网络共650000个神经元

3）VGG

（1）简要介绍

VGG是Visual Geometry Group, Department of Engineering Science,University of Oxford (牛津大学工程科学系视觉几何组)的缩写，2014年参ILSVRC(ImageNet Large Scale Visual Recognition Challenge) 2014大赛获得亚军(当年冠军为GoogLeNet，但因为VGG结构简单，应用性强，所以很多技术人员都喜欢使用基于VGG的网络)。

（2）主要参数

• 网络深度:16~19层
• 5组卷积-池化层，3个全连接层三个全连接层，前两层都有4096通道，第三层共1000路及代表1000个标签类别;最后一层为softmax层
• 所有卷积层有相同的配置，即卷积核大小为3×3，步长为1，填充为1
• 池化层区域大小2×2，步长为2

（3）网络结构

4）GoogleLeNet

其特点主要是GoogleInception

5）ResNet 残差网络

（1）简要介绍

• ResNet是ILSVRC2015大赛冠军，在ImageNet测试集上取得了3.57%的错误率
• 更深的网络结构，采用残差结构来缓解深度CNN的梯度消失问题

（2）网络结构

4 小节

本章节介绍了卷积神经网络(CNN)，CNN是深度学习的主要模型在解决复杂工程问题中表现出了良好的性能。卷积神经网络主要由以下几层构成

• 卷积层。执行卷积运算
• 激活层。对卷积结果执行激活函数运算
• 池化层。降低数据规模，防止过拟合
• 全连接层。执行输出计算

三、图像处理

3.1 图像色彩操作

1 图像色彩调整

1）亮度调整

• 对HSV空间的V分量进行处理可以实现对图像亮度的增强
• 直接将彩色图像灰度化，也可以得到代表图像亮度的灰度图进行图像处理，计算量比HSV颜色空间变化低。但在HSV空间中进行处理可以得到增强后的彩色图像
  

2）饱和度调整

• 对HSV空间的S分量进行处理可以实现对图像饱和度的增强。
• 饱和度的调整通常是在S原始值上乘以一个修正系数
• 修正系数大于1，会增加饱和度，使图像的色彩更鲜
• 明修正系数小于1，会减小饱和度，使图像看起来比较平淡
  

3） 色调调整

• 对HSV空间的H分量进行处理可以实现对图像色调的增强
• 色相H的值对应的是一个角度，并且在色相环上循环。所以色相的修正可能会造成颜色的失真
• 色相的调整通常在H原始值上加上一个小的偏移量，使其在色相环上有小角度的调整。调整后，图像的色调会变为冷色或者暖色。

2 图像灰度化

1）什么是图像灰度化

在RGB模型中，如果R=G=B时，则彩色表示一种灰度颜色，其中R=G=B的值叫灰度值，因此，灰度图像每个像素只需一个字节存放灰度值 (又称强度值、亮度值)灰度范围为0-255。将RGB图像（彩色图像）转换为灰度图像的过程称为图像灰度化处理。

2）如何进行图像灰度化

• 分量法。将彩色图像中的三分量的亮度作为三个灰度图像的灰度值可根据应用需要选取一种灰度图像。
• 最大值法。将彩色图像中的三分量亮度的最大值作为灰度图的灰度值。
• 将彩色图像中的三分量亮度求平均得到一个灰度值。
• 根据重要性及其它指标，将三个分量以不同的权值进行加权平均。例如，由于人眼对绿色的敏感最高，对蓝色敏感最低，因此，按下式对RGB三分量进行加权平均能得到较合理的灰度图像。

3 二值化与反二值化

1）二值化

二值化闯值处理是将原始图像处理为仅有两个值的二值图像，对于灰度值大于闽值t的像素点，将其灰度值设定为最大值。对于灰度值小于或等于值的像素点，将其灰度值设定为0。

2）反二值化

反二值化闯值处理的结果也是仅有两个值的二值图像，对于灰度值大于阀值的像素点，将其值设定为0;对于灰度值小于或等于闽值的像素点，将其值设定为255。

4 直方图均衡

1）图像直方图

• 灰度直方图反映的是一幅图像中各灰度级像素出现的频率。以灰度级为横坐标，纵坐标为灰度级的频率，绘制频率同灰度级的关系图就是灰度直方图。
• 它是图像的一个重要特征，反映了图像灰度分布的情况使用直方图进行图像变换是一种基于概率论的处理方法，通过改变图像的直方图修改图像中各像素的灰度值，达到增强图像视觉效果的目的。
• 相对于灰度变化只针对单独的像素点操作，直方图变化综合考虑了全图的灰度值分布。

2）直方图均衡化

• 直方图均衡化将原始图像的直方图，即灰度概率分布图，进行调整，使之变化为均衡分布的样式，达到灰度级均衡的效果，可以有效增强图像的整体对比度。
• 直方图均衡化能够自动的计算变化函数，通过该方法自适应得产生有均衡直方图的输出图像。
• 能够对图像过暗、过亮和细节不清晰的图像得到有效的增强在常用的图像处理库中，直方图操作都有API直接调用实现

5 代码实现

imread读取彩色图像，默认的色彩空间为BGR

1）读取、写入、显示等基本操作

# opencv核心库
pip3 install opencv-python==3.4.10.37  

# opencv贡献库
pip3 install opencv-contrib-python==3.4.10.37

import cv2 as cv

img = cv.imread('zebra.png')
print(img)

# 图像信息
print(img.shape)  # 高度，宽度，通道数

# 显示图像
cv.imshow("img1", img)
cv.imshow("img2", img)

# 保存图像
cv.imwrite('save.png', img)


# 主动进入阻塞等待，等待用户按下按键
cv.waitKey()
cv.destroyAllWindows()

2）灰度图像

（1）可逆转换操作

注意：此方式为惯用法，使用接口来转换，可以输出彩色和灰度图像

import cv2 as cv

img = cv.imread('zebra.png')

# 显示图像
cv.imshow("RGB", img)

img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
cv.imshow("Gray", img_gray)

print(img_gray.shape)


# 主动进入阻塞等待，等待用户按下按键
cv.waitKey()
cv.destroyAllWindows()

（2）不可逆转换操作

注意：此方式转为灰度图像后，就无法输出彩色图像了

import cv2 as cv

img = cv.imread('zebra.png', 0)  # 1为彩色，0为灰度，默认为：1

# 显示图像
cv.imshow("RGB", img)


# 主动进入阻塞等待，等待用户按下按键
cv.waitKey()
cv.destroyAllWindows()

3）直方图均衡

（1）灰度图像均衡

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

img = cv.imread('low.jpg', 0)

plt.figure('hist')

plt.subplot(2, 2, 1)
plt.imshow(img, cmap="gray")

plt.subplot(2, 2, 2)
plt.hist(img.ravel(), bins=256, range=[0, 256])

# 直方图均衡
img_equ = cv.equalizeHist(img)
plt.subplot(2, 2, 3)
plt.imshow(img_equ, cmap="gray")

plt.subplot(2, 2, 4)
plt.hist(img_equ.ravel(), bins=256, range=[0, 256])
plt.show()

cv.waitKey()
cv.destroyAllWindows()

（2）彩色图像均衡

BGR没有亮度通道，需要将BGR色彩空间转为YUV或HSV

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

img = cv.imread('low.jpg')
plt.figure('hist')

# 原始图像
plt.subplot(2, 2, 1)
plt.imshow(img, cmap="gray")

# 原始图像的直方图
plt.subplot(2, 2, 2)
plt.hist(img.ravel(), bins=256, range=[0, 256])

# 直方图均衡
hsv = cv.cvtColor(img, cv.COLOR_BGR2HSV)  # 先 BGR转HSV
hsv[..., 2] = cv.equalizeHist(hsv[..., 2])   # 再亮度均衡化
bgr = cv.cvtColor(hsv, cv.COLOR_HSV2BGR)   # 最后再从HSV转到BGR
plt.subplot(2, 2, 3)
plt.imshow(bgr, cmap="gray")

plt.subplot(2, 2, 4)
plt.hist(bgr.ravel(), bins=256, range=[0, 256])
plt.show()

cv.waitKey()
cv.destroyAllWindows()

4）颜色选择（提取）

import cv2 as cv
import numpy as np

im = cv.imread('opencv.jpg')
hsv = cv.cvtColor(im, cv.COLOR_BGR2HSV)

min_blue = np.array([110, 50, 50])
max_blue = np.array([130, 255, 255])

mask = cv.inRange(hsv, min_blue, max_blue)

cv.imshow('mask', mask)
cv.imshow('ori', im)

res = cv.bitwise_and(im, im, mask=mask)

cv.imshow('res', res)

cv.waitKey()
cv.destroyAllWindows()

5）二值化与反二值化

import cv2 as cv
import numpy as np

im = cv.imread('opencv.jpg', 0)
t, binary_im = cv.threshold(im, 127, 255, cv.THRESH_BINARY)  # 图像，阈值，大于阈值时转到哪个值，二值化

cv.imshow('ori', im)
cv.imshow('binary', binary_im)

cv.waitKey()
cv.destroyAllWindows()

import cv2 as cv
import numpy as np

im = cv.imread('opencv.jpg', 0)
t, binary_im = cv.threshold(im, 127, 255, cv.THRESH_BINARY_INV)  # 图像，阈值，大于阈值时转到哪个值，二值化

cv.imshow('ori', im)
cv.imshow('binary', binary_im)

cv.waitKey()
cv.destroyAllWindows()

3.2 图像形态操作

1 仿射与透视变换

1）仿射变换

仿射变换是指图像可以通过一系列的几何变换来实现 平移、旋转 、镜像 等多种操作。该变换能够保持图像的平直性和平行性。平直性是指图像经过仿射变换后，直线仍然是直线;平行性是指图像在完成仿射变换后，平行线仍然是平行线。

（1）平移

x:水平方向移动的像素值
y:竖直方向移动的像素值

import cv2
import numpy as np

# 平移
def translate(img, x, y):
    '''
    :param img:  原始图像
    :param x: 变换后图像的水平像素
    :param y: 变换后图像的垂直像素
    :return:
    '''

    # 平移矩阵
    M = np.float32([[1, 0, x],
                  [0, 1, y]])
    
    h, w = img.shape[:2]

    res = cv2.warpAffine(img, M, (w, h))
    return res


if __name__ == '__main__':
    img = cv2.imread('low.jpg')
    cv2.imshow('img', img)
    res = translate(img, 50, 50)
    cv2.imshow('img_y50', res)
    cv2.waitKey()
    cv2.destroyAllWindows()

（2）镜像

import cv2

img = cv2.imread("low.jpg")
img_ver = cv2.flip(img, 0)
img_hor = cv2.flip(img, 1)

cv2.imshow('img', img)
cv2.imshow('img_ver', img_ver)
cv2.imshow('img_hor', img_hor)

cv2.waitKey()
cv2.destroyAllWindows()

（3）旋转

,是旋转中心的坐标点.

import cv2
import numpy as np

# 旋转
def rotate(img, angle, center=None):
    h, w = img.shape[:2]
    if center is None:
        center = (w/2, h/2)

    # 生成旋转矩阵
    M = cv2.getRotationMatrix2D(center, angle, 1.0)
    res = cv2.warpAffine(img, M, (w, h))

    return res


if __name__ == '__main__':
    img = cv2.imread('low.jpg')
    cv2.imshow('img', img)
    res = rotate(img, 45)
    cv2.imshow('img_y50', res)
    cv2.waitKey()
    cv2.destroyAllWindows()

2）透视变换

透视变换是将图片投影到一个新的视平面，也称作投影映射。它是二维(x,y)到三维(X,Y,Z)，再到另一个二维(x’,y’)空间的映射相对于仿射变换，它提供了更大的灵活性，将一个四边形区域映射到另一个四边形区域(不一定是平行四边形)，透视变换可用于图像形状校正。

2 图像算数计算

1）图像加法

作用：

1. 图像加法可以用于多幅图像平均去除噪声
2. 图像加法实现水印的叠加:

图像减法是找出两幅图像的差异，可以在连续图像中可以实现消除背景和运动检测。

（1）直接相加

直接相加会导致图像非常亮，较暗的无法显示，所以一般使用按权重相加

import cv2 as cv

img_low = cv.imread('low.jpg')
img_high = cv.imread('high.jpg')
img_added = cv.add(img_low, img_high)

cv.imshow('img_low', img_low)
cv.imshow('img_high', img_high)
cv.imshow('img_added', img_added)

cv.waitKey()
cv.destroyAllWindows()

（2）按权重相加

import cv2 as cv

img_low = cv.imread('low.jpg')
img_high = cv.imread('high.jpg')
img_added = cv.addWeighted(img_low, 0.8, img_high, 0.2, 0)

cv.imshow('img_low', img_low)
cv.imshow('img_high', img_high)
cv.imshow('img_added', img_added)

cv.waitKey()
cv.destroyAllWindows()

addWeighted 的第5个参数是亮度调节量，在最终的图像上加上这个值。

2）图像减法

import cv2 as cv

img_low = cv.imread('low.jpg')
img_high = cv.imread('high.jpg')
img_added = cv.subtract(img_low, img_high)

cv.imshow('img_low', img_low)
cv.imshow('img_high', img_high)
cv.imshow('img_added', img_added)

cv.waitKey()
cv.destroyAllWindows()

3 图像缩放

1）图像缩小

图像缩小可以通过删除矩阵中的元素来实现，例如:下面的例子进行隔行、隔列删除后，高度、宽度均减小为原来的一半。

import cv2
import numpy as np

img = cv2.imread('low.jpg')
cv2.imshow('img', img)

# 缩小
h, w = img.shape[:2]
dst_size = (int(w/2), int(h/2))
res = cv2.resize(img, dst_size)
cv2.imshow('res', res)
cv2.waitKey()
cv2.destroyAllWindows()

2）图像放大

图像放大需要进行像素插入，常用的插值法有最邻近插值法和双线性插值法

• 最邻近插值法： 直接使用新的像素点(x’, y’)最近的整数坐标灰度值作为该点的值，该方法计算量小，但精确度不高，并且可能破坏图像中的线性关系
• 最近邻插值法： 双线性插值法:使用新的像素点(x’,y’)最邻近的四个像素值进行插值计算。

import cv2
import numpy as np

img = cv2.imread('low.jpg')
cv2.imshow('img', img)

# 缩小
h, w = img.shape[:2]
dst_size = (int(w*2), int(h*2))
res = cv2.resize(img, dst_size, interpolation=cv2.INTER_NEAREST)  # 放大时，默认使用双线性差值，此时是最近邻插值
cv2.imshow('NEAREST', res)
res = cv2.resize(img, dst_size, interpolation=cv2.INTER_LINEAR)  # 放大时，默认使用双线性差值,此时双线性差值，效果最好
cv2.imshow('NEAREST', res)
cv2.waitKey()
cv2.destroyAllWindows()

4 腐蚀与膨胀

1）腐蚀

腐蚀是最基本的形态学操作之一，它能够将图像的边界点消除，使图像沿着边界向内收缩，也可以将小于指定结构体元素的部分去除。腐蚀用来“收缩”或者“细化二值图像中的前景，借此实现去除噪声、元素分割等功能。

2）膨胀

图像膨胀(dilate)是指根据原图像的形状，向外进行扩充。如果图像内两个对象的距离较近，那么在膨胀的过程中，两个对象可能会连通在一起。膨胀操作对填补图像分割后图像内所存在的空白相当有帮助.

3）图像开运算

开运算进行的操作是先将图像腐蚀，再对腐蚀的结果进行膨胀。开运算可以用于去噪、计数等。

4）图像闭运算

闭运算是先膨胀、后腐蚀的运算，它有助于关闭前景物体内部的小孔，或去除物体上的小黑点，还可以将不同的前景图像进行连接

5）形态学梯度

形态学梯度运算是用图像的膨胀图像减腐蚀图像的操作，该操作可以获取原始图像中前景图像的边缘。

6）礼帽运算

礼帽运算是用原始图像减去其开运算图像的操作。礼帽运算能够获取图像的噪声信息，或者得到比原始图像的边缘更亮的边缘信息。

7）黑帽运算

黑帽运算是用闭运算图像减去原始图像的操作。黑帽运算能够获取图像内部的小孔或前景色中的小黑点，或者得到比原始图像的边缘更暗的边缘部分。

5 图像裁剪

1）随机裁剪

import cv2 as cv
import numpy as np


def random_crop(img, w_, h_):
    '''
    :param img: 图像对象
    :param w_: 裁剪后图像的宽度
    :param h_: 裁剪后图像的高度
    :return: 返回的新图像
    '''

    h, w = img.shape[0:2]
    y = np.random.randint(0, h - h_)
    x = np.random.randint(0, w - w_)
    return img[y: y+h_+1, x: x+w_+1]


if __name__ == '__main__':
    img = cv.imread('low.jpg')
    img_crop = random_crop(img, 250, 80)
    cv.imshow('croped', img_crop)
    cv.imshow('ori', img)

    cv.waitKey()
    cv.destroyAllWindows()

2）中心裁剪

import cv2 as cv


def center_crop(img, w_, h_):
    h, w = img.shape[0:2]
    start_y = int(h/2-h_/2)
    start_x = int(w/2-w_/2)
    end_y = int(h/2+h_/2)
    end_x = int(w/2+w_/2)
    return img[start_y:end_y+1, start_x:end_x+1]


if __name__ == '__main__':
    img = cv.imread('low.jpg')
    img_crop = center_crop(img, 200, 200)
    cv.imshow('croped', img_crop)
    cv.imshow('ori', img)

    cv.waitKey()
    cv.destroyAllWindows()

三、Tensorflow

3.1 Tensorflow概述

1. 什么是Tensorflow

TensorFlow由谷歌人工智能团队谷歌大脑(Google Brain)开发和维护的开源深度学习平台，是目前人工智能领域主流的开发平台，在全世界有着广泛的用户群体。

2. Tensorflow的特点

• 优秀的构架设计，通过“张量流”进行数据传递和计算，用户可以很容易地、可视化地看到张量流动的每一个环节
• 可轻松地在CPU/GPU上部署，进行分布式计算，为大数据分析提供计算能力的支撑
• 跨平台性好，灵活性强。TensorFlow不仅可在Linux、Mac和Windows系统中运行，甚至还可在移动终端下工作

3. 安装

pip3 install tensorflow==1.14.10   # CPU版本
pip3 install tf-nightly-gpu==1.14.10  # GPU版本

4. Tensorflow的体系结构

TensorFlow属于“定义”与“运行”相分离的运行机制。从操作层面以抽象成两种:模型构建和模型运行

• 客户端:用户编程、执行使用
• master:用来与客户端交互，并进行任务调度
• worker process: 工作节点，每个worker process可以访问一到多个device
• device: TF的计算核心，执行计算
  

5. 后端逻辑

6. 基本概念

1）张量

张量 (Tensor):多维数组或向量，张量是数据的载体，包含名字、形状、数据类型等属性。

2）数据流

• 数据流图(Data Flow Graph)用“结点(nodes)和“线”(edges)的有向图来描述数学计算
• “节点”一般用来表示数学操作，也可以表示数据输入 (feed in)的起点/输出(push out) 的终点，或者是读取/写入持久变量(persistent variable)的终点
• “线”表示“节点”之间的输入/输出关系。这些数据“线”可以输运多维数据数组，即“张量”(tensor)
• 一旦输入端的所有张量准备好，节点将被分配到各种计算设备完成异步并行地执行运算

3）操作

• 操作(Operation，简称op)指专门执行计算的节点，tensorflow函数或API定义的都是操作。常用操作包括:
  • 标量运算，向量运算，矩阵运算
  • 带状态的运算
  • 神经网络组建
  • 存储、恢复
  • 控制流
  • 队列及同步运算

4）图和会话

• 图(Graph)描述整个程序结构，Tensorflow中所有的计算都构建在图中
• 会话(Session)用来执行图的运算

5）变量

• 在Tensorflow中，变量(Variable) 是一种操作，变量是一种特殊的张量能够进行存储持久化(张量不能进行持久化)，它的值是张量
• 占位符(placeholder) 是变量占位符，当不能确定变量的值时，可以先声明一个占位符，真正执行时再传入变量

3.2 Tensorflow的基本使用

1 图

• 图(Graph)描述了计算的过程。TensorFlow 程序通常被组织成一个构建阶段和一个执行阶段。在构建阶段 op 的执行步骤 被描述成一个图在执行阶段使用会话执行执行图中的 op
• TensorFlow Python 库有一个默认图(default graph),op 构造器可以为其增加节点这个默认图对许多程序来说已经足够用了，也可以创建新的图来描述计算过程
• 在Tensorflow中，op/session/tensor都有graph属性

import tensorflow as tf


con1 = tf.constant(100.0)
con2 = tf.constant(200.0)
res = tf.add(con1, con2)

# 查看默认的图
default_graph = tf.get_default_graph()
print(default_graph)

with tf.Session() as sess:
    print(sess.run(res))
    print(con1.graph)
    print(con2.graph)
    print(res.graph)
    print(sess.graph)

程序输出：
300.0
<tensorflow.python.framework.ops.Graph object at 0x0000027EBEA94148>
<tensorflow.python.framework.ops.Graph object at 0x0000027EBEA94148>
<tensorflow.python.framework.ops.Graph object at 0x0000027EBEA94148>
<tensorflow.python.framework.ops.Graph object at 0x0000027EBEA94148>

2 会话及相关操作

会话(session)用来执行图中的计算，并且保存了计算张量对象的上下文
信息。会话的作用主要有

• 运行图结构
• 分配资源
• 掌握资源(如变量、队列、线程)
  一个session只能执行一个图的运算。可以在会话对象创建时，指定运行的图。如果在构造会话时未指定图形参数，则将在会话中使用默认图。如果在同一进程中使用多个图(使用tf.graph()创建)，则必须为每个图使用不同的会话，但每个图可以在多个会话中使用。

1）创建会话

tf.Session()  # 使用默认的图

2）运行

session.run(fetches, feed_dict=None)

fetches： 图中的单个操作，或多个操作的列表
feed_dict： 运行传入的参数构成的字典，可以覆盖之前的值，

3）关闭

session.close()

import tensorflow as tf


con1 = tf.constant(100.0)
con2 = tf.constant(200.0)
res = tf.add(con1, con2)

# 查看默认的图
default_graph = tf.get_default_graph()
print(default_graph)

# 新建一个图
new_graph = tf.Graph()

# op只能加在默认的图上，可以暂时将新建的图暂时设为默认的图，然后再释放
with new_graph.as_default(): # 临时设为默认的图
    new_opp = tf.constant('hello world!')

with tf.Session(graph=new_graph) as sess:
    # print(sess.run([con1, con2, res]))
    print(sess.run(new_opp))

op只能加在默认的图上，可以暂时将新建的图暂时设为默认的图，然后再释放

3 张量

1）张量的阶与形状

阶:张量的维度(数方括号的层数)形状表示方法

• 0维:()
• 1维:(5)，1行5个元素
• 2维:(2,3)，2行3列
• 3维:(2,34)两个3行4列的矩阵

2）张量的数据类型

3）张量的常用属性

4）张量类型转换

import tensorflow as tf

tensor_2d = tf.ones([3, 3], dtype='int32')
tensor_zero = tf.zeros([3, 3])
tensor_2_string = tf.cast(tensor_zero, tf.string)  # 浮点型不能转换成字符串

with tf.Session() as sess:
    print(tensor_2d.eval())
    print(tensor_2_string.eval())  # 浮点型不能转换成字符串，此处报错

注意：浮点型不能转换成字符串

5）张量形状的改变

（1）静态张量

在创建一个张量，初始状态的形状

• tf.Tensorget_shape0:获取Tensor对象的静态形状
• tf.Tensorset shape():更新Tensor对象的静态形状

注意: 转换静态形状的时候，1-D到1-D，2-D到2-D，不能跨阶数改变形状对于已经固定或者设置静态形状的张量/变量，不能再次设置静态形状

（2）动态张量

动态形状:在运行图时，动态形状才是真正用到的，这种形状是一种描述原始张量在执行过程中的一种张量

tf.reshape(tf.Tensorshape):创建一个具有不同动态形状的新张量可以跨纬度转换，如1D–>2D,1D–>3D

import tensorflow as tf
import numpy as np

tensor_2d = tf.placeholder('float32', shape=[None, 4])
data = np.arange(0, 8).reshape(2, 4)

new_data = tf.reshape(data, [1, 8])

with tf.Session() as sess:
    print(sess.run(new_data))

4）张量数学操作

import tensorflow as tf
import numpy as np

x = tf.constant(np.arange(1, 5).reshape(2, 2), dtype='float32')
y = tf.constant(np.arange(5, 1, -1).reshape(2, 2), dtype='float32')

add = tf.add(x, y)
matmul = tf.matmul(x, y)
log = tf.log(x)
reduce_mul = tf.reduce_mean(x, axis=1)

z = tf.constant(np.arange(1, 8), dtype='float32')
seg = tf.constant([0, 0, 0, 1, 1, 2, 2])
res = tf.segment_sum(z, seg)


with tf.Session() as sess:
    print(x.eval(), y.eval())
    print(sess.run(add))
    print(sess.run(matmul))
    print(sess.run(log))
    print(sess.run(reduce_mul))
    print(res.eval())

输出：
[[1. 2.]
[3. 4.]]

[[5. 4.]
[3. 2.]]
[[6. 6.]
[6. 6.]]
[[11. 8.]
[27. 20.]]
[[0. 0.6931472]
[1.0986123 1.3862944]]
[1.5 3.5]
[ 6. 9. 13.]

4 占位符

不确定张量内容情况下，可以使用占位符先占个位置，然后执行计算时，通过参数传入具体数据执行计算(通过feed dict参数指定)。placeholder节点被声明的时候是未初始化的，也不包含数据，如果没有为它供给数据，则TensorFlow运算的时候会产生错误。

#占位符定义:
name = tf.placeholder(dtype, shape=None, name=None)

import tensorflow as tf
import numpy as np

tensor_2d = tf.placeholder('float32', shape=[2, 3])
data = np.arange(0, 6).reshape(2, 3)

with tf.Session() as sess:
    print(sess.run(tensor_2d, feed_dict={tensor_2d: data}))

占位符数据可变

import tensorflow as tf
import numpy as np

tensor_2d = tf.placeholder('float32', shape=[None, 3])
data = np.arange(0, 9).reshape(3, 3)

with tf.Session() as sess:
    print(sess.run(tensor_2d, feed_dict={tensor_2d: data}))

5 变量

• 变量是一种op，它的值是张量
• 变量能够持久化保存，普通张量则不
• 可当定义一个变量时，需要在会话中进行初始化
• 变量创建

tf.Variable(initial_value=None, name=None)

import tensorflow as tf
import numpy as np

var = tf.Variable(tf.random_normal([3, 4]))
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init_op)  # 必须初始化
    print(var.eval())

3.3 可视化

• 可视化是用来查看在Tensorflow平台下程序运行的过程，包括: 张量变量，操作，数据流，学习过程等，从而方便 TensorFlow 程序的理解调试与优化
• Tensorflow提供了专门的可视化工具tensorboard，它将tensorflow执行的数据、模型、过程用图形方式进行显示。tensorflow在执行过程中可以通过某些操作，将模型、数据、graph等信息，保存到磁盘中的Events文件中去，从而提供给tensorboard进行可视化

1 启动tensorboard

tensorboard --logdir=D:\Project\PythonProject\ML_Learning\summary\

注意：
（1）路径不加引号
（2）网址：http://localhost:6006/

2 摘要与事件文件操作

如果需要将变量/张量在tensorboard中显示，需要执行以下两步

• 收集变量
  tf.summary.scalar(name, tensor) # 收集标量，name为名字，tensor为值
  tf.summary.histogram(name, tensor)# 收集高维度变量参数
  tf.summary.image(name, tensor)# 收集图片张量
• 合并变量并写入事件文件
  merged = tf.summary.merge_all()# 合并所有变量
  summary = sess. run(merged) # 行合并，每次迭代训练都需要运行
  FileWriter.add_summary(summary,i) # 添加摘要，i表示第几次的值

3 最简单的线型回归实例

import tensorflow as tf
import numpy as np


# 模型 y = 3x + 11

# 1.准备数据
x = tf.random_normal([100, 1], mean=1.75, stddev=0.5, name='x_data')
y = tf.matmul(x, [[3.0]]) + 11.0

# 2.构建模型 y = wx + b
weight = tf.Variable(tf.random_normal([1, 1]), name="w", trainable=True)
bias = tf.Variable(0.0, name="b", trainable=True)
y_pred = tf.matmul(x, weight) + bias

# 3.损失函数
loss = tf.reduce_mean(tf.square(y_pred - y), axis=0)

# 4. 梯度下降
optimizer = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

# 初始化全局变量
init_var = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init_var)
    print("weight: {}, bias: {}".format(weight.eval(), bias.eval()))
    for i in range(500):
        sess.run(optimizer)
        print("i: {}, weight: {}, bias: {}, loss: {}".format(i, weight.eval()[0, 0], bias.eval(), loss.eval()[0]))

输出：
weight: [[1.7854646]], bias: 0.0
i: 0, weight: 6.423867225646973, bias: 2.6243207454681396, loss: 9.109596252441406
i: 1, weight: 7.046351909637451, bias: 3.0945069789886475, loss: 4.743853569030762
i: 2, weight: 7.123383522033691, bias: 3.241851329803467, loss: 3.4027130603790283
i: 3, weight: 7.111809730529785, bias: 3.3871138095855713, loss: 3.7377519607543945
i: 4, weight: 7.076264381408691, bias: 3.4926016330718994, loss: 4.294710159301758
i: 5, weight: 6.986569404602051, bias: 3.5605499744415283, loss: 3.821505069732666
i: 6, weight: 6.944016456604004, bias: 3.637892484664917, loss: 3.1669256687164307
i: 7, weight: 7.036805629730225, bias: 3.7961792945861816, loss: 4.031221866607666
i: 8, weight: 6.889873504638672, bias: 3.842052698135376, loss: 3.933861494064331
i: 9, weight: 6.9066009521484375, bias: 3.9894847869873047, loss: 4.430022716522217
i: 10, weight: 6.641869068145752, bias: 3.951720952987671, loss: 3.121511936187744
i: 11, weight: 6.720321178436279, bias: 4.120347499847412, loss: 3.2809276580810547
…
i: 489, weight: 3.013960599899292, bias: 10.974303245544434, loss: 5.876861541764811e-05
i: 490, weight: 3.0138514041900635, bias: 10.974569320678711, loss: 4.3935862777289e-05
i: 491, weight: 3.0136618614196777, bias: 10.974894523620605, loss: 4.670991620514542e-05
i: 492, weight: 3.013606309890747, bias: 10.975181579589844, loss: 4.826369695365429e-05
i: 493, weight: 3.013457775115967, bias: 10.975468635559082, loss: 5.3314353863243014e-05
i: 494, weight: 3.012927770614624, bias: 10.975626945495605, loss: 4.780766539624892e-05
i: 495, weight: 3.012622594833374, bias: 10.975756645202637, loss: 5.1373455789871514e-05
i: 496, weight: 3.0128049850463867, bias: 10.976174354553223, loss: 4.308684583520517e-05
i: 497, weight: 3.0126736164093018, bias: 10.976405143737793, loss: 5.3000025218352675e-05
i: 498, weight: 3.01277494430542, bias: 10.97690486907959, loss: 4.385461943456903e-05
i: 499, weight: 3.012420892715454, bias: 10.97700023651123, loss: 3.047487734875176e-05

3.4 模型的保存在加载

模型训练可能是一个很长的过程，如果每次执行预测之前都重新训练，会非常耗时，所以几乎所有人工智能框架都提供了模型保存与加载功能，使得模型训练完成后，可以保存到文件中，供其它程序使用或继续训练。

模型保存与加载通过tf.train.Saver对象完成，实例化对象:

saver = tf.train.Saver(var_list=None, max_to_keep=5)

var_list: 要保存和还原的变量，可以是一个dict或一个列表
max_to_keep:要保留的最近检查点文件的最大数量。创建新文件时，会删除较旧的文件(如max_to_keep=5表示保留5个检查点文件)
保存: saver.save(sess，/tmp/ckpt/model)
加载: saver.restore(sess，/tmp/ckpt/model)

模型保存与加载实例

import tensorflow as tf
import os


# 模型 y = 3x + 11

# 1.准备数据
x = tf.random_normal([100, 1], mean=1.75, stddev=0.5, name='x_data')
y = tf.matmul(x, [[3.0]]) + 11.0

# 2.构建模型 y = wx + b
weight = tf.Variable(tf.random_normal([1, 1]), name="w", trainable=True)
bias = tf.Variable(0.0, name="b", trainable=True)
y_pred = tf.matmul(x, weight) + bias

# 3.损失函数
loss = tf.reduce_mean(tf.square(y_pred - y))

# 4. 梯度下降
optimizer = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

# 初始化全局变量
init_var = tf.global_variables_initializer()

# 收集数据
tf.summary.scalar('loss', loss)
merged = tf.summary.merge_all()

# 模型保存对象
saver = tf.train.Saver()

with tf.Session() as sess:
    sess.run(init_var)
    print("weight: {}, bias: {}".format(weight.eval(), bias.eval()))
    fw = tf.summary.FileWriter('./summary/', graph=sess.graph)

    #
    if os.path.exists('./model/linear_model/checkpoint'):
        saver.restore(sess, './model/linear_model/')

    for i in range(100):
        sess.run(optimizer)
        summary = sess.run(merged)
        fw.add_summary(summary, i)
        print("i: {}, weight: {}, bias: {}, loss: {}".format(i, weight.eval()[0, 0], bias.eval(), loss.eval()))

    # 训练结束之后保存
    saver.save(sess, './model/linear_model/')

3.5 文件读取机制

TensorFlow文件读取分为三个步骤：
第一步：将要读取的文件放入文件名队列
第二步：读取文件内容，并实行解码
第三步：批处理，按照指定笔数构建成一个批次取出

• 文件队列构造:生成一个先入先出的队列，文件阅读器会需要它来读取数据

tf.train.string_input_producer(string_tensor, shuffle=True)

string_tensor：含有文件名的一阶张量
shuffle：是否打乱文件顺序
返回：文件队列

3 文件读取

• 文本文件读取

tf.TextLineReader

读取CSV文件，默认按行读取

• 二进制文件读取

tf.FixedLengthRecordReader(record_bytes)

读取每个记录是固定字节的二进制文件

• record_bytes：每次读取的字节数

• 通用读取方法

read(file_queue)

从队列中读取指定数量(行，字节)的内容
返回值:一个tensor元组， (文件名, value)

4 文件内容解码

• 解码文本文件

tf.decode_csv(records, record_defaults)

将CSV文件内容转换为张量，与tf.TextLineReader搭配使用

• records：字符串，对应文件中的一行
• record_defaults：类型

返回：tensor对象列表

• 解码二进制文件

tf.decode_raw(input_bytes,out_type)

将字节转换为由数字表示的张量，与tf.FixedLengthRecordReader搭配使用

• input_bytes： 待转换字节
• out_type：输出类型

返回: 转换结果

5 读取csv文件

import os
import tensorflow as tf


def read_csv(filelist):
    # 1.构造文件队列
    file_queue = tf.train.string_input_producer(filelist)

    # 2.定义文件读取器
    reader = tf.TextLineReader()

    # 3.读取数据
    filename, data = reader.read(file_queue)

    # 4.解码
    records = [["None"], ["None"]]
    example, label = tf.decode_csv(data, records)

    # 5.分批次输出
    example_bat, label_bat = tf.train.batch([example, label], batch_size=10, num_threads=1)  # batch_size: 一批次读取数据的大小

    return (example_bat, label_bat)


if __name__ == '__main__':
    # 构建文件列表
    dir_name = './data/'
    file_names = os.listdir(dir_name)
    file_list = [os.path.join(dir_name, file_name) for file_name in file_names]
    ret_example_bat, ret_label_bat = read_csv(file_list)
    with tf.Session() as sess:
        # 定义线程协调器
        coord = tf.train.Coordinator()

        # 开启文件读取线程
        threads = tf.train.start_queue_runners(sess, coord)
        print(sess.run([ret_example_bat, ret_label_bat]))
        coord.request_stop()
        coord.join(threads)

6 读取图像

1）图像文件读取API（全文件读取器）

图像读取器

tf.WholeFileReader

`功能:：将文件的全部内容作为值输出的reader

read方法：读取文件内容，返回文件名和文件内容

图像解码器

tfimage.decode jpeg(constants) # 解码jpeg格式
tf.image.decode_png(constants) # 解码png格式

返回值：3-D张量，[height, width,channels]

修改图像大小

tf.image.resize(images,size) # 

images： 图片数据，3-D或4-D张量

• 3-D:[长，宽，通道]
• 4-D:[数量,长，宽，通道

size：1-Dint32张量，[长、宽] (不需要传通道数)

2）实例

import tensorflow as tf
import os
import matplotlib.pyplot as plt


def read_img(filelist):
    # 1.构造文件队列
    file_queue = tf.train.string_input_producer(filelist)

    # 2.定义文件读取器
    reader = tf.WholeFileReader()

    # 3.读取数据
    filename, data = reader.read(file_queue)

    # 4.解码
    images = tf.image.decode_jpeg(data)

    # 5.分批次输出
    images_resized = tf.image.resize(images, (200, 200))
    images_resized.set_shape([200, 200, 3])
    images_bat = tf.train.batch([images_resized], batch_size=10, num_threads=1)  # batch_size: 一批次读取数据的大小

    return images_bat


if __name__ == '__main__':
    # 构建文件列表
    dir_name = './test_img/'
    file_names = os.listdir(dir_name)
    file_list = [os.path.join(dir_name, file_name) for file_name in file_names]
    images_batch = read_img(file_list)
    with tf.Session() as sess:
        # 定义线程协调器
        coord = tf.train.Coordinator()

        # 开启文件读取线程
        threads = tf.train.start_queue_runners(sess, coord)
        res = sess.run(images_batch)
        coord.request_stop()
        coord.join(threads)
        print(res)

    plt.figure()
    for i in range(10):
        plt.subplot(2, 5, i+1)
        plt.xticks([])
        plt.yticks([])
        plt.imshow(res[i].astype('int32'))

    plt.show()

3.6 MNIST

• 手写数字的数据集，来自美国国家标准与技术研究所(Nationallnstitute of Standards andTechnology，NIST)，发布与1998年
• 样本来自250个不同人的手写数字，50%高中学生，50%是人口普查局的工作人员
• 数字从0~9，图片大小是28×28像素，训练数据集包含60000个样本，测试数据集包含10000个样本。数据集的标签是长度为10的一维数组数组中每个元素索引号表示对应数字出现的概率
• 下载地址：http://yann.lecun.com/exdb/mnist/

1 基础版本

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np

# 1.数据准备
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])

# 2.模型构建
weight = tf.Variable(tf.random_normal([784, 10]), trainable=True)
bias = tf.Variable(tf.ones([10]), trainable=True)
pred_y = tf.nn.softmax(tf.matmul(x, weight) + bias)

# 3.损失函数
cross_entropy = - tf.reduce_sum(y * tf.log(pred_y), reduction_indices=1)  # reduction_indices 求和
cost = tf.reduce_mean(cross_entropy)

# 4.梯度下降
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

# 5.定义模型保存对象
saver = tf.train.Saver()
model_path = './model/mnist/mnist_model.ckpt'

batch_size = 100  # 批次大小
total_batch = int(mnist.train.num_examples / batch_size)

# 6.开始执行
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    for epoch in range(100):
        avg_cost = 0.0
        for i in range(total_batch):
            # 从训练集中拿到一个批次的数据
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            params = {x: batch_xs, y: batch_ys}
            opt_value, costs_value = sess.run([optimizer, cost], feed_dict=params)
            avg_cost += (costs_value / total_batch)
        print('epoch:{}, cost: {}'.format(epoch+1, avg_cost))
    print("训练结束")

    # 模型评估
    corr_pre = tf.equal(tf.argmax(pred_y, 1), tf.argmax(y, 1))
    acc = tf.reduce_mean(tf.cast(corr_pre, tf.float32))
    acc_res = acc.eval({x: mnist.test.images, y: mnist.test.labels})

    save_path = saver.save(sess, model_path)
    print("准确率：", acc_res)
    print("模型已保存至：", save_path)

# 测试
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    saver.restore(sess, model_path)

    # 从测试集读取样本
    batch_xs, batch_ys = mnist.test.next_batch(10)
    output = tf.argmax(pred_y, 1)
    out_val, pred_label = sess.run([output, pred_y], feed_dict={x: batch_xs, y: batch_ys})

    print('预测结果：', out_val)
    print("真实结果: ", np.argmax(batch_ys, axis=1))

2 增量训练+结果显示版本

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
import os
import matplotlib.pyplot as plt

# 1.数据准备
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])

# 2.模型构建
weight = tf.Variable(tf.random_normal([784, 10]), trainable=True)
bias = tf.Variable(tf.ones([10]), trainable=True)
pred_y = tf.nn.softmax(tf.matmul(x, weight) + bias)

# 3.损失函数
cross_entropy = - tf.reduce_sum(y * tf.log(pred_y), reduction_indices=1)  # reduction_indices 求和
cost = tf.reduce_mean(cross_entropy)

# 4.梯度下降
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

# 5.定义模型保存对象
saver = tf.train.Saver()
model_path = './model/mnist/'

batch_size = 100  # 批次大小
total_batch = int(mnist.train.num_examples / batch_size)

# 6.开始执行
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    if os.path.exists('./model/mnist/checkpoint'):
        saver.restore(sess, model_path)

    for epoch in range(100):  # 训练100轮
        avg_cost = 0.0
        for i in range(total_batch):
            # 从训练集中拿到一个批次的数据
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            params = {x: batch_xs, y: batch_ys}
            opt_value, costs_value = sess.run([optimizer, cost], feed_dict=params)
            avg_cost += (costs_value / total_batch)
        print('epoch:{}, cost: {}'.format(epoch+1, avg_cost))
    print("训练结束")

    # 模型评估
    corr_pre = tf.equal(tf.argmax(pred_y, 1), tf.argmax(y, 1))
    acc = tf.reduce_mean(tf.cast(corr_pre, tf.float32))
    acc_res = acc.eval({x: mnist.test.images, y: mnist.test.labels})

    save_path = saver.save(sess, model_path)
    print("准确率：", acc_res)
    print("模型已保存至：", save_path)

# 测试
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    saver.restore(sess, model_path)

    # 从测试集读取样本
    batch_xs, batch_ys = mnist.test.next_batch(10)
    output = tf.argmax(pred_y, 1)
    out_val, pred_label = sess.run([output, pred_y], feed_dict={x: batch_xs, y: batch_ys})

    print('预测结果：', out_val)
    real_ret = np.argmax(batch_ys, axis=1)
    print("真实结果: ", real_ret)

    plt.figure('num')
    for i in range(10):
        plt.subplot(2, 5, i+1)
        plt.xticks([])
        plt.yticks([])
        plt.imshow(batch_xs[i].reshape(-1, 28))
        plt.title('pred:{}, real:{}'.format(out_val[i], real_ret[i]))
    plt.show()