散点图
散点图是指在回归分析中,数据点在直角坐标系平面上的分布图,散点图表示因变量随自变量而变化的大致趋势,据此可以选择合适的函数对数据点进行拟合。用两组数据构成多个坐标点,考察坐标点的分布,判断两变量之间是否存在某种关联或总结坐标点的分布模式。散点图将序列显示为一组点。值由点在图表中的位置表示。类别由图表中的不同标记表示。散点图通常用于比较跨类别的聚合数据,其应用有很多,总结两个常见的应用如下:
- 回归分析。散点图用于回归分析中,数据点在直角坐标系平面上的分布图,散点图表示因变量随自变量而变化的大致趋势,据此可以选择合适的函数对数据点进行拟合。散点图经过回归分析之后,可以对相关对象进行预测分析,能让我们发现变量之间隐藏的关系,进而做出科学的决策,而不是模棱两可。比如,下面房价的散点图可以为我们直观呈现不同城市的房价上涨情况,为后续的房价政策调整做出重要的支持。
- 相关分析。散点图用于相关性分析中,用两组数据构成多个坐标点,考察坐标点的分布,判断两变量之间是否存在某种关联或总结坐标点的分布模式。通过观察散点图上数据点的分布情况,我们可以推断出变量间的相关性。如果变量之间不存在相互关系,那么在散点图上就会表现为随机分布的离散的点,如果存在某种相关性,那么大部分的数据点就会相对密集并以某种趋势呈现。变量间的关系有很多,如线性关系、指数关系、对数关系等等,当然,没有关系也是一种重要的关系。
1.scatter()
我们使用pyplot 中的 scatter() 方法来绘制散点图。scatter() 方法语法格式如下:
matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, *, edgecolors=None, plotnonfinite=False, data=None, **kwargs)
2.参数说明
x,y:长度相同的数组,也就是我们即将绘制散点图的数据点,输入数据。
s:点的大小,默认 20,也可以是个数组,数组每个参数为对应点的大小。
c:点的颜色,默认蓝色 ‘b’,也可以是个 RGB 或 RGBA 二维行数组。
| 颜色标记 | 描述 |
|---|---|
| ‘r’ | red |
| ‘g’ | green |
| ‘b’ | blue |
| ‘c’ | cyan |
| ‘m’ | magenta |
| ‘y’ | yellow |
| ‘k’ | black |
| ‘w’ | white |
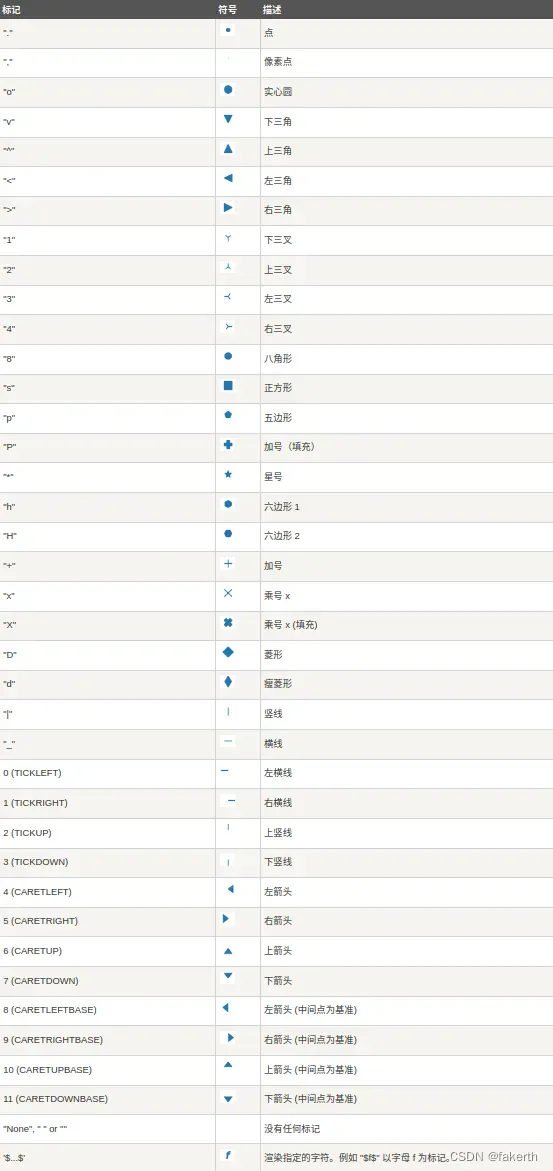
marker:点的样式,默认小圆圈 ‘o’。
cmap:Colormap,默认 None,标量或者是一个 colormap 的名字,只有 c 是一个浮点数数组的时才使用。如果没有申明就是 image.cmap。
norm:Normalize,默认 None,数据亮度在 0-1 之间,只有 c 是一个浮点数的数组的时才使用。
vmin,vmax::亮度设置,在 norm 参数存在时会忽略。
alpha::透明度设置,0-1 之间,默认 None,即不透明。
linewidths::标记点的长度。
edgecolors::颜色或颜色序列,默认为 ‘face’,可选值有 ‘face’, ‘none’, None。
plotnonfinite::布尔值,设置是否使用非限定的 c ( inf, -inf 或 nan) 绘制点。
**kwargs::其他参数。
基本x-y坐标
import matplotlib.pyplot as plt
import numpy as np
x = np.array([5,7,8,7,2,17,2,9,4,11,12,9,6])
y = np.array([99,86,87,88,111,86,103,87,94,78,77,85,86])
plt.scatter(x, y, color = 'r',marker='v')
x = np.array([2,2,8,1,15,8,12,9,7,3,11,4,7,14,12])
y = np.array([100,105,84,105,90,99,90,95,94,100,79,112,91,80,85])
plt.scatter(x, y, color = 'b',marker='*')
plt.title(" TITLE")
plt.xlabel("x - label")
plt.ylabel("y - label")
plt.show()
分类比较
import matplotlib.pyplot as plt
import numpy as np
x = np.array([177, 185, 166, 160, 175, 176, 157, 154, 141, 191])
y = np.array(["Type A"] * 10)
plt.scatter(x, y, color='b')
meanA = x.mean()
x = np.array([178, 179, 180, 190, 188, 174, 156, 192, 189, 179])
y = np.array(["Type B"] * 10)
plt.scatter(x, y, color='r')
meanB = x.mean()
x = np.array([162, 168, 167, 155, 176, 197, 173, 158, 178, 190])
y = np.array(["Type C"] * 10)
plt.scatter(x, y, color='g')
meanC = x.mean()
x = np.array([meanA, meanB, meanC])
y = np.array(["mean"] * 3)
color = np.array(["b", "r", "g"])
plt.scatter(x, y, color=color)
# plt.axhline(y=,ls=":",c="yellow")#添加水平直线
for i, j in zip(x, color):
plt.axvline(x=i, ls="-", c=j) # 添加垂直直线
for i in range(len(x)):
plt.annotate('%s' % x[i], xy=(x[i], y[i]))
plt.xlabel("performance")
plt.ylabel("Type")
plt.title('compare A B C')
plt.show()
# plt.savefig("compare.png")
文章出处登录后可见!
已经登录?立即刷新