站点图标 AI技术聚合

【机器学习技巧】回归模型的几个常用评估指标（R2、Adjusted-R2、MSE、RMSE、MAE、MAPE）及其在sklearn中的调用方式

乘风

目录

  • 回归模型评估的两个方面
    • 1. 预测值的拟合程度
    • 2. 预测值的准确度
  • 以糖尿病数据集的回归模型为计算示例-计算各指标
  • 1. 决定系数R2
    • 1.1 R2求解方式一—-从metrics调用r2_socre
    • 1.2 R2求解方式二—-从模型调用score
    • 1.3 R2求解方式二—-交叉验证调用scoring=r2
  • 2. 校准决定系数Adjusted-R2
  • 3.均方误差MSE（Mean Square Error）
  • 4.均方根误差RMSE（Root Mean Square Error）
  • 5.平均绝对误差MAE（Mean Absolute Error）
  • 6. 平均绝对百分比误差MAPE（Mean Absolute Percentage Error）

回归模型评估的两个方面

回归模型的评估主要有以下两个方面：

1. 预测值的拟合程度

拟合程度就是我们的预测值是否拟合了足够的信息。在回归模型中，我们经常使用决定系数R2来进行度量。

2. 预测值的准确度

准确度指预测值与实际真实值之间的差异大小。常用均方误差（Mean Squared Error, MSE）,平均绝对误差（Mean Absolute Error, MAE）,平均绝对百分比误差MAPE来度量。

下面我们对这几个评估指标进行介绍，以及其在sklearn中如何使用。

以糖尿病数据集的回归模型为计算示例-计算各指标

# 导入线性回归器算法模型
from sklearn.linear_model import LinearRegression 
import numpy as np
#糖尿病数据集 ，训练一个回归模型来预测糖尿病进展
from sklearn import datasets
dia = datasets.load_diabetes()
# 提取特征数据和标签数据
data = dia.data
target = dia.target
# 训练样本和测试样本的分离，测试集20%
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(data,target,test_size=0.2)
# 创建线性回归模型
linear = LinearRegression()
# 用linear模型来训练数据:训练的过程是把x_train 和y_train带入公式W = (X^X)-1X^TY求出回归系数W
linear.fit(x_train,y_train)
# 对测试数据预测
y_pre = linear.predict(x_test)

1. 决定系数R2

R2( Coefficient of determination)：决定系数，反映的是模型的拟合程度，R2的范围是0到1。其值越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好。

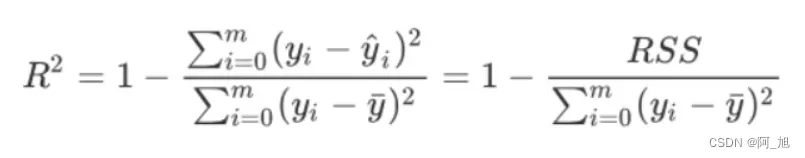
1.1 R2求解方式一—-从metrics调用r2_socre

from sklearn.metrics import r2_score
r2 = r2_score(y_true=y_test,y_pred=y_pre)
r2

0.5439247940652986

1.2 R2求解方式二—-从模型调用score

r2 = linear.score(x_test,y_test)
r2

0.5439247940652986

1.3 R2求解方式二—-交叉验证调用scoring=r2

from sklearn.model_selection import cross_val_score
r2 = cross_val_score(linear,x_test,y_test,cv=10,scoring="r2").mean()  # 求的值n次交叉验证后r2的均值
r2

0.3803655235719364

2. 校准决定系数Adjusted-R2

校正决定系数是指决定系数R可以用来评价回归方程的优劣，但随着自变量个数的增加，R2将不断增大。Adjusted-R2主要目的是为了抵消样本数量对R2的影响。

其中，n为样本数量，p为特征数量。即样本为n个[ x1, x2, x3, … , xp, y ]。取值也是越接近1越好。

n, p = x_test.shape
adjusted_r2 = 1 - ((1 - r2) * (n - 1)) / (n - p - 1)
adjusted_r2

0.300925206081159

3.均方误差MSE（Mean Square Error）

均方误差（Mean Square Error, MSE）：是真实值与预测值的差值的平方，然后求和的平均，一般用来检测模型的预测值和真实值之间的偏差

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_pre)#y_test为实际值，y_pre为预测值

2658.8312775325517

4.均方根误差RMSE（Root Mean Square Error）

均方根误差（Root Mean Square Error, RMSE）：即均方误差开根号，方均根偏移代表预测的值和观察到的值之差的样本标准差

from sklearn.metrics import mean_squared_error
np.sqrt(mean_squared_error(y_test,y_pre))#y_test为实际值，y_pre为预测值

51.563856309750065

5.平均绝对误差MAE（Mean Absolute Error）

平均绝对误差（Mean Absolute Error, MAE）：是绝对误差的平均值，可以更好地反映预测值误差的实际情况

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test,y_pre)#y_test为实际值，y_pre为预测值

42.09538057884898

6. 平均绝对百分比误差MAPE（Mean Absolute Percentage Error）

平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）：是相对误差度量值，它使用绝对值来避免正误差和负误差相互抵消，可以使用相对误差来比较各种时间序列模型预测的准确性。理论上，MAPE 的值越小，说明预测模型拟合效果越好，具有更好的精确度。

在这里插入图片描述

from sklearn.metrics import mean_absolute_percentage_error
mean_absolute_percentage_error(y_test,y_pre)#y_test为实际值，y_pre为预测值

0.4062288709549193

如果内容对你有帮助，感谢点赞+关注哦！

更多干货内容持续更新中…

文章出处登录后可见！

已经登录？立即刷新
退出移动版