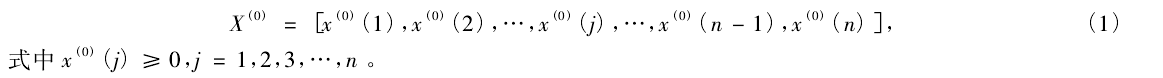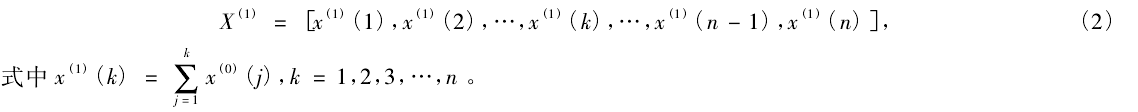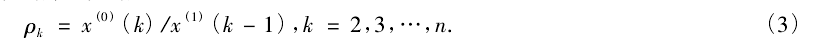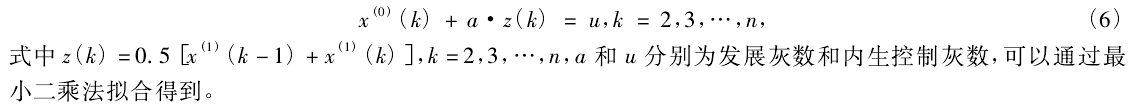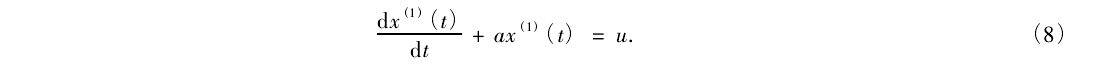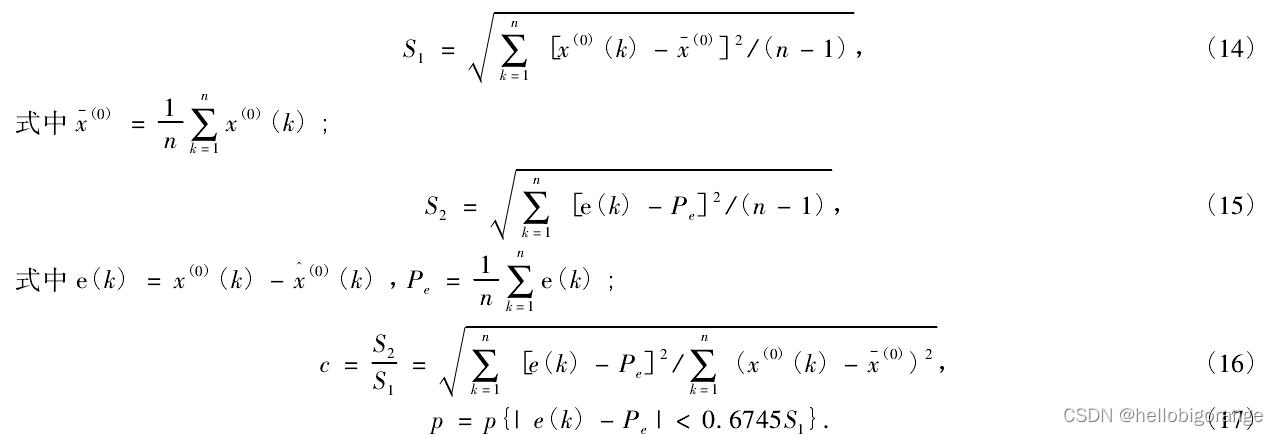灰色系统理论及其应用系列博文：
一、灰色关联度分析法(GRA)_python
二、灰色预测模型GM(1,1)
三、灰色预测模型GM(1,n)
四、灰色预测算法改进1—背景值Z
五、灰色预测改进2—三角残差拟合

一、灰色预测法

灰色预测模型是通过少量的、不完全的信息，建立数学模型并做出预测的一种预测方法。灰色系统理论建模采用的是先对原始数据列做生成处理再成立微分方程模型。是处理小样本（4个就可以）预测问题的有效工具，而对于小样本预测问题回归和神经网络的效果都不太理想。

最简单的模型是GM(1,1)，G：Grey（灰色）；M：模型；(1,1)：只含有单变量的一阶微分方程模型。

GM(1,1)首先对原始非负离散数据进行一个一阶累加处理（白化过程），然后对这组数据利用最小二乘法（和线性回归的方式十分类似）求解灰色系数，利用灰色系数构建灰色微分方程，求解微分方程既可以得到拟合公式。

灰色预测适用条件：用于时间短、数据资料少、数据不需要典型的分布规律、计算量较低、对短期预测有较高精度。不适合随机波动较大的数据。gm(1,1)适合白化后是指数趋势的数据（这样构建的微分方程的解才更适合拟合指数数据），灰色预测是利用趋势建模。

1.1 算法

（1）建立原始非负数据序列

（2）对原始数据集合​进行分布特征检验以后，采用一次累加进行累加数据生成（累加能使灰色过程变白 ），获取新的数据序列如式

（3）判断数据是否适合采用GM(1,1)

方法一：准光滑序列检验（论文的方法）：
判断数据是否为准光滑序列，采用光滑比分析原始数据光滑性，光滑比:数据变化越平稳，越小

定义，若满足对任意n，有，则我们称是 可以作为GM(1,1)的数据而被灰度预测的。

（4）建立的灰微分方程

（5）用最小二乘求解模型的发展灰数a，内生控制参量u，令，用最小二乘法可得

其中，累加矩阵 A 和常数向量 B如下

（6）将新的数据序列​ 表示为一阶微分方程的形式，并求解微分方程

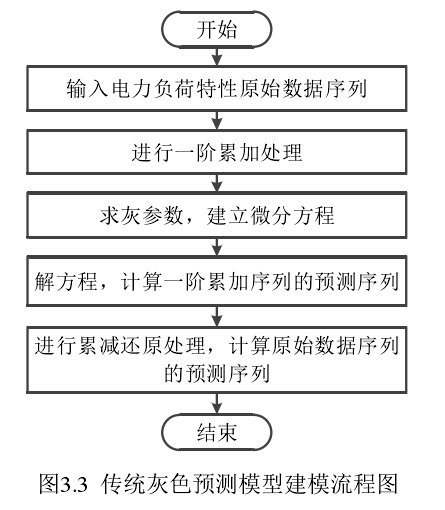
（7）测模型的精确度取决于均方差比 c 与小误差概率 p 的大小。后验差比 c 表明预测值与实际值误差的大小，其值越小则误差越小。小误差概率 p 是指即残差与残差均值的差值的绝对值小于 0. 674 5 倍原始数据均方差的概率，其值大，则表示精度高。计算方式如下：

1.2 使用注意

微分方程模型作为灰色系统理论预测用的模型，其主要凭借以下几点
（1）灰色系统理论把原始数列在固定范围变化的灰色量，认定随过程是在一定时区、一定范围内变化的灰色过程。
（2）一阶微分方程有着指数增长形式的解值，无规律的原始数列经过累加生成得到累加数列后，此数列也具备指数增加的规律。灰色模型是生成的数据数列所建模型。
（3）灰色系统理论可建立GM(1，n)模型来解决高阶系统建模问题。一阶微分方程所组成的灰色模型称为GM模型群。
（4）GM模型采用累加生成做生成处置，为了获得预测的数据，由GM模型所得的数据对其进行逆生成处理，即累减生成还原处理。
（5）在灰色系统理论中，为了提高预测精度，可以对数据进行合适的取舍、对灰数采用不同的生成方式和调节残差的级别来实现。

1.3 案例及代码

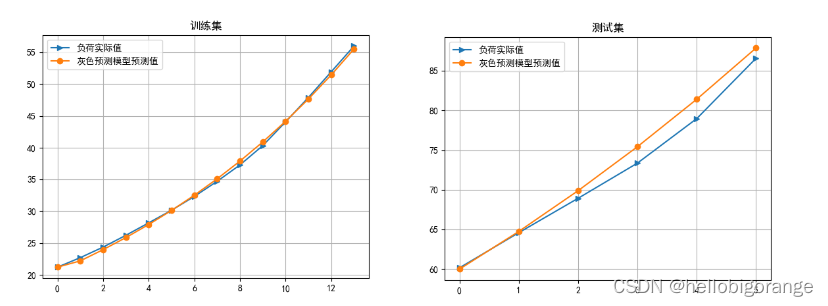
以江苏省无锡市锡北镇电力负荷预测为例，给出灰度预测的结果

• 原始数据

# -*- coding: utf-8 -*- 
# @Time : 2022/3/18 14:18 
# @Author : Orange
# @File : g_pred.py.py

from decimal import *


class GM11():
    def __init__(self):
        self.f = None

    def isUsable(self, X0):
        '''判断是否通过光滑检验'''
        X1 = X0.cumsum()
        rho = [X0[i] / X1[i - 1] for i in range(1, len(X0))]
        rho_ratio = [rho[i + 1] / rho[i] for i in range(len(rho) - 1)]
        print("rho:", rho)
        print("rho_ratio:", rho_ratio)
        flag = True
        for i in range(2, len(rho) - 1):
            if rho[i] > 0.5 or rho[i + 1] / rho[i] >= 1:
                flag = False
        if rho[-1] > 0.5:
            flag = False
        if flag:
            print("数据通过光滑校验")
        else:
            print("该数据未通过光滑校验")

        '''判断是否通过级比检验'''
        lambds = [X0[i - 1] / X0[i] for i in range(1, len(X0))]
        X_min = np.e ** (-2 / (len(X0) + 1))
        X_max = np.e ** (2 / (len(X0) + 1))
        for lambd in lambds:
            if lambd < X_min or lambd > X_max:
                print('该数据未通过级比检验')
                return
        print('该数据通过级比检验')

    def train(self, X0):
        X1 = X0.cumsum()
        Z = (np.array([-0.5 * (X1[k - 1] + X1[k]) for k in range(1, len(X1))])).reshape(len(X1) - 1, 1)
        # 数据矩阵A、B
        A = (X0[1:]).reshape(len(Z), 1)
        B = np.hstack((Z, np.ones(len(Z)).reshape(len(Z), 1)))
        # 求灰参数
        a, u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(A)
        u = Decimal(u[0])
        a = Decimal(a[0])
        print("灰参数a：", a, "，灰参数u：", u)
        self.f = lambda k: (Decimal(X0[0]) - u / a) * np.exp(-a * k) + u / a

    def predict(self, k):
        X1_hat = [float(self.f(k)) for k in range(k)]
        X0_hat = np.diff(X1_hat)
        X0_hat = np.hstack((X1_hat[0], X0_hat))
        return X0_hat

    def evaluate(self, X0_hat, X0):
        '''
        根据后验差比及小误差概率判断预测结果
        :param X0_hat: 预测结果
        :return:
        '''
        S1 = np.std(X0, ddof=1)  # 原始数据样本标准差
        S2 = np.std(X0 - X0_hat, ddof=1)  # 残差数据样本标准差
        C = S2 / S1  # 后验差比
        Pe = np.mean(X0 - X0_hat)
        temp = np.abs((X0 - X0_hat - Pe)) < 0.6745 * S1
        p = np.count_nonzero(temp) / len(X0)  # 计算小误差概率
        print("原数据样本标准差：", S1)
        print("残差样本标准差：", S2)
        print("后验差比：", C)
        print("小误差概率p：", p)


if __name__ == '__main__':
    import matplotlib.pyplot as plt
    import numpy as np

    plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
    plt.rcParams['axes.unicode_minus'] = False  # 步骤二（解决坐标轴负数的负号显示问题）

    # 原始数据X
    X = np.array(
        [21.2, 22.7, 24.36, 26.22, 28.18, 30.16, 32.34, 34.72, 37.3, 40.34, 44.08, 47.92, 51.96, 56.02, 60.14,
         64.58,
         68.92, 73.36, 78.98, 86.6])
    # 训练集
    X_train = X[:int(len(X) * 0.7)]
    # 测试集
    X_test = X[int(len(X) * 0.7):]

    model = GM11()
    model.isUsable(X_train)  # 判断模型可行性
    model.train(X_train)  # 训练
    Y_pred = model.predict(len(X))  # 预测
    Y_train_pred = Y_pred[:len(X_train)]
    Y_test_pred = Y_pred[len(X_train):]
    score_test = model.evaluate(Y_test_pred, X_test)  # 评估

    # 可视化
    plt.grid()
    plt.plot(np.arange(len(X_train)), X_train, '->')
    plt.plot(np.arange(len(X_train)), Y_train_pred, '-o')
    plt.legend(['负荷实际值', '灰色预测模型预测值'])
    plt.title('训练集')
    plt.show()

    plt.grid()
    plt.plot(np.arange(len(X_test)), X_test, '->')
    plt.plot(np.arange(len(X_test)), Y_test_pred, '-o')
    plt.legend(['负荷实际值', '灰色预测模型预测值'])
    plt.title('测试集')
    plt.show()

数据通过光滑校验
该数据通过级比检验
灰参数a： -0.0764631383879229853395287364037358202040195465087890625 ，灰参数u： 19.73534371303100698469279450364410877227783203125
原数据样本标准差： 9.683763042674403
残差样本标准差： 1.0311971065218763
后验差比： 0.10648723042660145
小误差概率p： 1.0

可视化

二、复现论文《基于灰色系统理论的贵阳市城市用水总量预测》

2.1 数据：

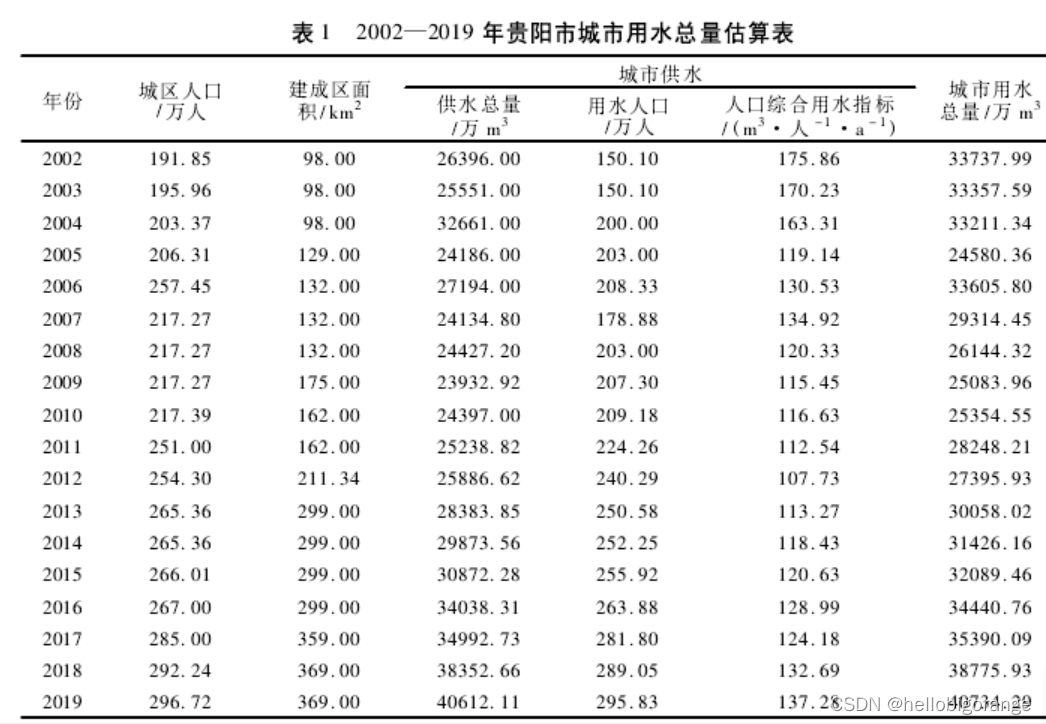
data.csv
年份,城区人口,建成区面积,供水总量,用水人口,人口综合用水指标,城市用水总量
2002, 191.85, 98.00, 26396.00, 150.10, 175.86, 33737.99
2003, 195.96, 98.00, 25551.00, 150.10, 170.23, 33357.59
2004, 203.37, 98.00, 32661.00, 200.00, 163.31, 33211.34
2005, 206.31, 129.00, 24186.00, 203.00, 119.14, 24580.36
2006, 257.45, 132.00, 27194.00, 208.33, 130.53, 33605.80
2007, 217.27, 132.00, 24134.80, 178.88, 134.92, 29314.45
2008, 217.27, 132.00, 24427.20, 203.00, 120.33, 26144.32
2009, 217.27, 175.00, 23932.92, 207.30, 115.45, 25083.96
2010, 217.39, 162.00, 24397.00, 209.18, 116.63, 25354.55
2011, 251.00, 162.00, 25238.82, 224.26, 112.54, 28248.21
2012, 254.30, 211.34, 25886.62, 240.29, 107.73, 27395.93
2013, 265.36, 299.00, 28383.85, 250.58, 113.27, 30058.02
2014, 265.36, 299.00, 29873.56, 252.25, 118.43, 31426.16
2015, 266.01, 299.00, 30872.28, 255.92, 120.63, 32089.46
2016, 267.00, 299.00, 34038.31, 263.88, 128.99, 34440.76
2017, 285.00, 359.00, 34992.73, 281.80, 124.18, 35390.09
2018, 292.24, 369.00, 38352.66, 289.05, 132.69, 38775.93
2019, 296.72, 369.00, 40612.11, 295.83, 137.28, 40734.29

2.2 使用灰色预测预测供水总量及城市用水总量

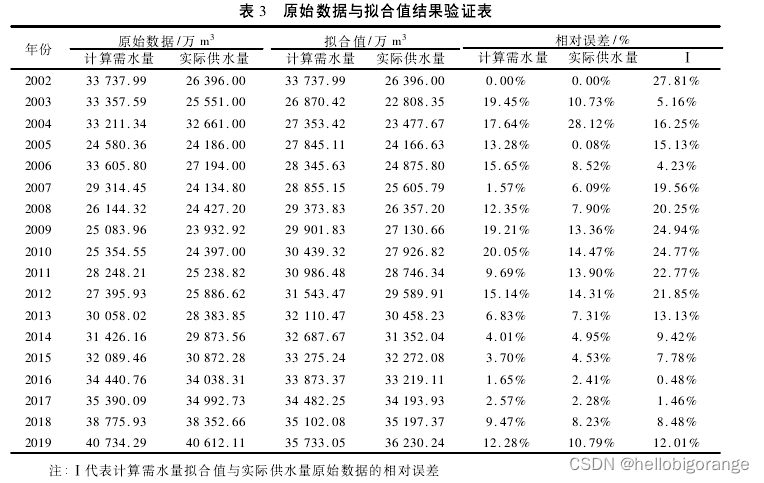
采用1.3的代码复现结果与论文的完全一致，因此下面就直接放了论文的结果。
以 2002—2019 年各年间估算的城市用水总量( 计算需水量) 与供水总量( 实际供水量) 为原始数据序
列，运用 GM(1,1) 模型分别得到原始数据序列的响应式。

以贵阳市 2002—2019 年各年间供水总量 ( 实际供水量) 计算灰色预测模型，得到各关键参数如下:

结果分析

以供水总量( 实际供水量) 组成的原始数据所计算的 c 值和 p 值均符合灰色预测的范围，精度检验结果信度可靠; 另一方面，模型预测的相对误差 0. 087 8 ＜ 0. 10，预测精度为91. 22% ，GM（1,1） 预测模型可运用于预测贵阳市城市用水总量。

另一方面，由于城市用水总量原始数据的波动较大，因此 GM( 1，1) 预测后的数据方差也较大，从而导致模型的后验差检验的 c值较大，p 值较小。GM(1,1)预测不满足要求。

比较可以发现以供水总量( 实际供水量) 组成的原始数据序列 X( 0)的响应式模型精度较高，原因在于实际供水量更符合一定时期内供需平衡的客观规律，而计算需水量受人口综合用水指标的影响较大，人口综合用水指标与一定时期内的经济发展水平、人口流动等因素有关。

一些问题补充

1、为什么灰色预测使用的数据量少？

灰色预测对数据白话的处理是累加处理，不会造成数据损失，因此可以在数据量较少的情况下建模。像是一些时序模型，如arima可能会对数据差分处理，进一步造成数据损失，有些模型对数据的分布有要求，这本身就需要较大的数据量
为什么说灰色系统预测方法所需样本数据量少？

2、灰色预测为啥要用微分方程拟合，原理是什么？

第二个回答的PPT很赞，灰色预测为什么需要用微分方程拟合