目录
碰撞检测——GJK算法
1.GJK算法的原理及思想
GJK算法是由 Gilbert,johnson和 Keerthi 3人在1988年共同开发的一类迭代算法。GJK算法的输入为两物体的顶点集,通过有限次数的迭代后,最后输出结果为两物体之间的欧氏距离。根据两物体之间 的欧氏距离,可进行碰撞检测。当两物体之间的距离等于或者小于零时,可判定两物体发生碰撞。基于距离跟踪的Gilbert-Johnson-Keerth(简称GJK)碰撞算法是通过支持映射来计算空间中两个凸体间距的渐进算法。
1.1 Minkowski Sum(明可夫斯基和)
GJK算法中使用了明可夫斯基和的概念。假设有两个物体,它们的明可夫斯基和就是物体1上的所有点和物体2上的所有点的和集。用公式表示就是:
A + B = {a + b|a∈A, b∈B}
如果两个物体都是凸体,它们的明可夫斯基和也是凸体。
对于减法,明可夫斯基和的概念也成立,这时也可称作明可夫斯基差。
A – B = A + (-B) = {a + (– b)|a∈A, b∈B} = {a – b)|a∈A, b∈B}
如果两个形状重叠,进行Minkowski Sum后的形状包含原点。Minkowski Sum的运算是shape A的每个顶点和shape B的所有顶点求和(或求差)。所得到点的外包络即是运算所得形状。
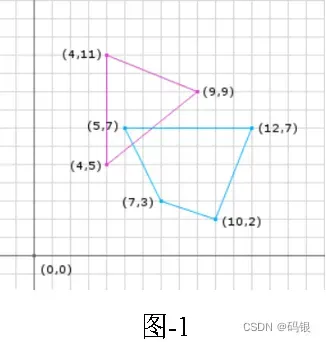
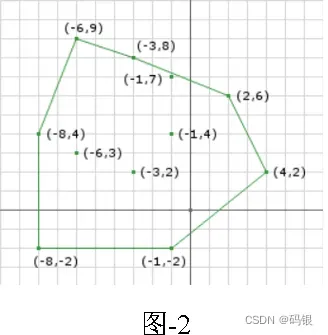
1.2 Simplex
单纯形是代数拓扑中的基本概念,单纯形是三角形和四面体的一种泛化,一个k 维单纯形是指包含(k+1)个节点的凸多面体。不需要计算Minkowski Sum,只需要计算Minkowski Sum是否包含原点,如果包含原点则两个形状重叠,否则不重叠。在Minkowski Sum得到的形状中迭代的构建Simplex,判断Simplex是否包含原点,包含则重叠,否则不重叠。
1.3 support函数
support函数返回两个形状Minkowski Sum的一个点用以构建Simplex,shape1的点减去shape2的点可以得到一个Minkowski Sum的一个点,但我们不希望得到重复的点。使用support函数得到shape在一个direction(方向)上的最远点,然后在不同的方向上得到另一个不同的点。在direction上选择最远点可以使生成的Simplex的面积最大化以增加包含原点的几率增加算法收敛速度。使用这种方法得到的点在Minkowski Sum的边上,因此如果得到的点不包含原点则Minkowski Sum不包含原点。
Public Point support(Shape shape1, Shape shape2, Vector d) {
// d is a vector direction(doesn't have to normalized)
// get points on the edge of the shapes in opposite direction
Point p1 = shape1.getFarthestPointInDirection(d);
Point p2 = shape2.getFarthestPointInDirection(d.negative());
// perform the Minkowski Sum
Point p3 = p1.subtract(p2);
// p3 is now a point in Minkowski space on the edge of the Minkowski Difference
return p3;
}
1.4 构建Simplex
首先选择三个点构造Simplex,如果包含原点,则两个多边形重叠,否则重新选择点构建新的Simplex。由support函数可知,需要一个direction来选择Minkowski Sum点,任意的direction都是可以的,但是选择两个多边形的中心点的向量方向是较优的选择。
Vector d = // choose a search direction
// get the first Minkowski Difference point
Simplex.add(support(A, B, d));
// negate d for the next point
d.negate();
// start looping
while (true) {
// add a new point to the simplex because we haven't terminated yet
Simplex.add(support(A, B, d));
// make sure that the last point we added actually passed the origin
if (Simplex.geLast().dot(d) <= 0) {
// if the point added last was not past the origin in the direction of d
// then the Minkowski Sum cannot possibly contain the origin since
// the last point added is on the edge of Minkowski Difference
return false;
} else {
// otherwise we need to determine if the origin is in the current simplex
if (Simplex.contains(ORIGIN)) {
// if it does then we know there is a collision
return true;
} else {
// otherwise we cannot be certain so find the edge who is closest to the
// origin and use its normal (in the direction of the origin) as the new
// d and continue the loop
d = getDirection(Simplex);
}
}
}
Simplex.geLast().dot(d) <= 0的解释:
Simplex最新得到的点是Minkowski Sum在给定方向上的最远点,如果这个点没有enclose原点,则Minkowski Sum不会包含原点。如下图,direction是( 1 , 0 ) (-1, 0)(-1,0),点p ( 1, – 4 ) p(1, 4)p(1, -4)是在direction上的最远点。点p在d上的投影是-1,原点在d dd上的投影是0,由于p是Minkowski Sum是最远点,所以其不会包含原点
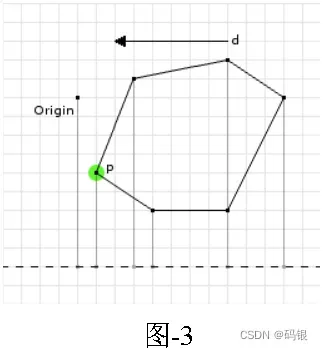
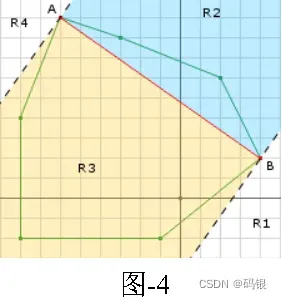
当得到两个Minkowski Sum点时,如图-4,B是第一个点,A 是第二个点,A 和B是Minkowski Sum包络上的点,如果origin在R1或者R4区域,则Minkowski Sum不包含原点,Simplex.geLast().dot(d) <= 0返回true。由图可知,origin在R3区域内,因此需要计算AB的petualar vector应该指向R3。
AB=B−A
AO=O−A
perp=(AB×AO)×AB
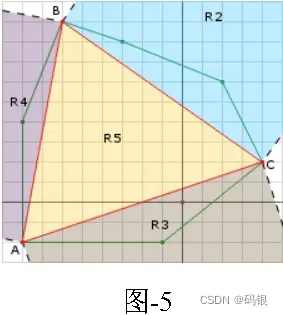
如图-5,此时support函数得到新的Minkowski Sum点A,点B是第二点(图-4中的A ),点C 是第一个点(图-4中的B),origin可能存在于R3、R4和R5中,计算( A C × A B ) × A B生成ABperp,计算ABprep⋅(AO)判断origin是否在R4,计算(AB×AC)×AC生成ACperp,计算ACperp⋅(AO)判断origin是否在R3。
Vector d = // choose a search direction
// get the first Minkowski Sum point
Simple.add(support(A, B, d));
// nagate d for the next point
d.negate();
// start loop
while (true) {
// add a new point to the simplex because we haven't terminated yet
Simple.add(support(A, B d));
// make sure that the last point added actually passed the origin
if (Simple.getLast().dot(d) <= 0) {
// if the point added last was not past the origin in the direction of d
// then the Minkowski Sum cannot possibly contain the origin since
// the last point added is on the edge of Minkowski Difference
return false;
} else {
// otherwise determine if the origin is in the current simplex
if (containsOrigin(Simple, d)) {
// if it does, there is a collision
return true;
}
}
}
public boolean containOrign(Simples s, Vector d) {
// get the last point added to the simplex
a = Simplex.getLast(); // the last point
// compute AO (same thing as -A)
ao = a.negate();
if (Simplex.points.size == 3) {
// in triangle case
// get point B and C
b = Simplex.getB(); // the second point
c = Simplex.getC(); // the first point
// compute the edges
ab = b - a;
ac = c - a;
// compute the normals
abPerp = tripleProduct(ac, ab, ab);
acPerp = tripltProdect(ab, ac, ac);
// is the origin in R4
if (adPerp.dot(ao) > 0) {
// remove point C
Simplex.remove(c);
// set the new direction to ABPerp
d.set(abPerp);
} else {
// is the origin in R3
if (acPerp.dot(ao) > 0) {
// remove point B
Simples.remove(b);
// set the new direction to ACPerp
d.set(acPerp);
} else {
// otherwise origin in R5, there is a collision
return true;
}
}
} else {
// in line segment case
b = Simplex.getB();
// compute AB
ab = b -a;
// get the perp to AB in the direction of the origin
abPerp = tripleProduct(ab, ao, ab);
// set the direction to ABPerp
d.set(abPerp);
}
return false;
}
2. GJK算法步骤
1.选取初始方向,初始方向可以是两个多边形的中心点构成的矢量,也可以是两个多边形各自选取一个顶点构成的
矢量,还可以是给定的任意矢量;
2.根据初始方向,用Support函数得到第一个support点,并放到单纯形(simplex)中;
3.将初始方向取反,作为下一-次迭代方向;
4.循环开始:
a)根据迭代方向和Support函数计算出一个新的support点;
b)若新的support点与迭代方向的点乘结果小于0 ,说明在这个迭代方向上,已经无法找到一个能够跨越原
点的support点了。也就是说,无法组成一个能够包含原点的单纯形。 即两个多边形不相交,函数退出;
c)若新的support点能够跨越原点,则将其加到simplex中;
d)更新单纯形和迭代方向,并判断simplex是否包含原点。这时simplex有两个点或三个点:
若为两个点,则这两个点构成一条直线,以该直线的垂线朝向原点的方向,作为下一次迭代方向;
若为三个点,则需要判断这三个点组成的三角形是否包含原点。若不包含,则保留离原点最近的边上的两个点,同样以这两个点的直线的垂线朝向原点的方向,作为下一次迭代方向。
回到循环的开始步骤a。
3. GJK算法的优缺点分析
优点:
基于GJK模型的算法有快速,易实施,且适用于多种凸体的优点。
它是一种迭代方法,但是收敛速度非常快,如果使用最终的穿透/分离向量进行约束,则可以在几乎恒定的时间内运行。
它可以支持实现“support ”函数的任何形状。因此不需要增加特殊的代码或算法来处理弯曲的形状。
缺点:
仅能在凸包上运行,数学模型复杂(需要有一定的线性空间,线性代数的知识),且难以理解。
线段是一种十分简单的单形体,用GJK算法进行距离计算太繁琐。
4. GJK算法与其他相关算法的比较分析
4.1 GJK算法和SAT算法的比较
分离轴定理(Separating Axis Theorem,SAT)是一种可用于精确判断两个物体是否相交的算法,不仅适用于 Box(矩形),还适用于凸多边形。SAT用来检测两个凸多边形是否相交,也可以用于检测点是否在凸多边形内。凸多边形内的点的连线上的点都在凸多边形内,或者连线只和图多边形相交两次(边界处)。
GJK与SAT一样,仅在凸包上运行。GJK更具吸引力的功能之一是,它可以支持实现“support ”函数的任何形状。因此,与SAT不同,您不需要增加特殊的代码或算法来处理弯曲的形状。
GJK是一个迭代算法,但是如果事先给出穿透/分离向量,则它的收敛会很快,可以在常量时间内完成。在3D环境中,GJK可以取代SAT算法。GJK算法的最初目的是计算两个凸体之间的距离,在两个物体穿透深度比较小的情况下,可用它判定物体之间的碰撞。它也可以和别的算法相结合,用来检测两个物体之间深度穿透时候的碰撞情况。
4.2 GJK算法和EPA算法的比较
EPA,扩展多边形算法(Epanding Polytop Algorithm) ,用来计算两个多边形碰撞的穿透深度和方向,可用于将两个发生碰撞的多边形分离。当碰撞发生时,原点到最近的闵可夫斯基差集多边形的边(下文称作“差集最近边”)的距离,就是穿透深度,原点到该边的垂直向量就是穿透向量的方向。因此,核心问题就转换成了,如何求得距离原点最近的差集边。当碰撞检测完毕后,我们会得到一个单形体(Simplex),该单形体可能包含两个或三个support点,将这些support点首尾相连构成封闭的多边形。EPA算法每次迭代的时候,从这个多边形中选择一条最近的边,沿着该边的法线方向(原点到边的垂线方向),向外扩展。直到某条边无法向外扩展时,则该边就是差集最近边。
EPA算法和GJK求最近距离算法很相似,都是在找一个差集最近边。不过EPA用于发生碰撞的情况下,GJK求最近距离用于没有发生碰撞的情况下。理论上EPA也可以用于求两个多边形的最近边,只不过EPA收敛的速度没有GJK算法快。
参考资料
参考资料:http://www.dyn4j.org/2010/04/gjk-gilbert-johnson-keerthi/
版权声明:本文为CSDN博主「小作坊钳工」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:http://t.csdn.cn/6Vmyo
游蓝海的这篇文章:http://t.csdn.cn/dxWdx
由上述文章参考并修改
文章出处登录后可见!
