快速傅里叶变换-通过python代码实战讲解
注:该文适合在jupyter notebook编辑器上演示
FFT介绍
FT、DFT、FFT的关系:
傅里叶变换(FT)是针对连续信号的,不适用于离散信号。而实际测得的信号(如振动、电流等)都是不连续即离散的,这个时候离散傅里叶变换(DFT)出现了,用来针对离散信号的做傅里叶变换。但是DFT从数学上计算是可行的,但给计算机计算,比较复杂,因此J.W.库利和T.W.图基提出了快速傅里叶变换 (FFT), 其目的是利用计算机来高效、快速计算离散傅里叶变换。
适用范围
周期性信号,平稳信号(简单可理解其频率不随时间变化)
通过python代码来理解FFT
先产生一段正弦信号 y=sin(2_π_f*t) ,这里信号频率f=2
import numpy as np # 导入numpy包
import matplotlib.pyplot as plt # 导入matplotlib.pyplot包
t = np.linspace(start=0, stop=10, num=100) # 采样频率fs=100÷10=10
y = 4*np.sin(2*np.pi*t*2) # y=sin(2*π*f*t) # 这里f=2
plt.plot(t, y) # 绘制图形
plt.xlabel('t(s)')
plt.ylabel('f(Hz)')
plt.title('y=sin(2*π*2*t)')
输出结果
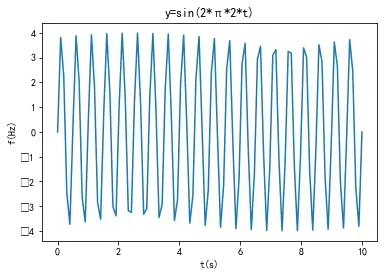
这里有两个问题:
第一,纵坐标的-1,-2,-3和-4的负号未能显示完全,这是因为python不能显示负号和中文。
第二,这个正弦信号不光滑,比较尖锐,这是因为采样频率为10,分辨率比较低。
改进后的时域信号
import numpy as np # 导入numpy包
import matplotlib.pyplot as plt # 导入matplotlib.pyplot包
import matplotlib
t = np.linspace(start=0, stop=10, num=1000) # 采样频率fs=1000÷10=10
y = 4*np.sin(2*np.pi*t*2) # y=sin(2*π*f*t) # 这里f=2
matplotlib.rcParams['axes.unicode_minus']=False #用来正常显示正负号
plt.plot(t, y) # 绘制图形
plt.xlabel('t(s)')
plt.ylabel('f(Hz)')
plt.title('y=sin(2*π*2*t)')
输出结果
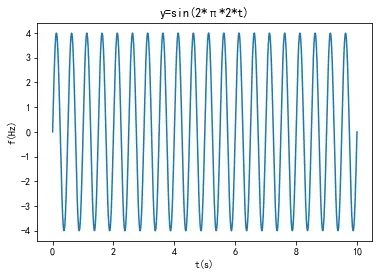
现在采样频率为100,生成的信号和正弦信号很像了
现在就开始对这个离散信号做FFT变换,看看效果
####----进行fft---####
matplotlib.rcParams['axes.unicode_minus']=False #用来正常显示正负号
t = np.linspace(start=0, stop=10, num=1000) # 采样频率fs=1000÷10=10
y = 4*np.sin(2*np.pi*t*2) # y=sin(2*π*f*t) # 这里f=2
# 画时域图
ax1 = plt.subplot(1, 2, 1)
plt.plot(t, y)
plt.xlabel('t(s)')
plt.ylabel('f(Hz)')
plt.title('y=sin(2*π*2*t) 时域图')
# 画fft图
fs = 100 # 采样频率
xf = np.fft.fft(y) # 对离散数据y做fft变换得到变换之后的数据xf
xfp = np.fft.fftfreq(len(y), d=1 / fs) # fftfreq(length,fs),计算得到频率
xf = abs(xf) # 将复数求模,得到fft的幅值
ax1 = plt.subplot(1, 2, 2)
plt.plot(xfp, xf) # 画fft图像,横坐标为频率,纵坐标为幅值
plt.xlabel('f(Hz)')
plt.ylabel('Amp')
plt.title('y=sin(2*π*2*t)p fft图')
输出结果
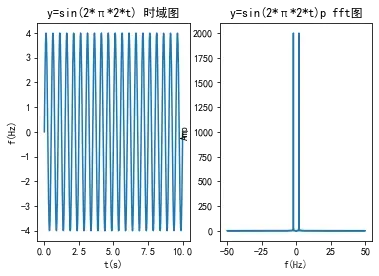
从fft图中可以看出这两个重要的现象
第一,频率存在负数,且其图像关于0Hz对称。在-2Hz和2Hz的地方存在很大的幅值
第二,频率是从-50Hz到50Hz(这个也是很重要的一点,fft得到的频率是采样频率的一半)
我们现在观察一下xf和xfp的值
print(xf) #这是幅值
array([1.91846539e-13, 2.00035896e-01, 4.03098512e-01, 6.12369070e-01,
8.31354662e-01, 1.06409657e+00, 1.31544309e+00, 1.59142838e+00,
1.89982442e+00, 2.25098029e+00, 2.65915286e+00, 3.14471294e+00,
3.73799357e+00, 4.48641986e+00, 5.46873781e+00, 6.82624293e+00,
8.84061181e+00, 1.21663574e+01, 1.87537300e+01, 3.82003257e+01,
1.99767920e+03, 4.18093223e+01, 2.11642707e+01, 1.43606392e+01,
1.09658841e+01, 8.92699589e+00, 7.56418128e+00, 6.58718456e+00,
5.85121855e+00, 5.27597074e+00, 4.81330295e+00, 4.43260128e+00,
4.11346328e+00, 3.84176526e+00, 3.60741741e+00, 3.40301801e+00,
...
1.99767920e+03, 3.82003257e+01, 1.87537300e+01, 1.21663574e+01,
8.84061181e+00, 6.82624293e+00, 5.46873781e+00, 4.48641986e+00,
3.73799357e+00, 3.14471294e+00, 2.65915286e+00, 2.25098029e+00,
1.89982442e+00, 1.59142838e+00, 1.31544309e+00, 1.06409657e+00,
8.31354662e-01, 6.12369070e-01, 4.03098512e-01, 2.00035896e-01])
print(xfp) #这是频率值
array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8,
0.9, 1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7,
1.8, 1.9, 2. , 2.1, 2.2, 2.3, 2.4, 2.5, 2.6,
2.7, 2.8, 2.9, 3. , 3.1, 3.2, 3.3, 3.4, 3.5,
3.6, 3.7, 3.8, 3.9, 4. , 4.1, 4.2, 4.3, 4.4,
4.5, 4.6, 4.7, 4.8, 4.9, 5. , 5.1, 5.2, 5.3,
...
47.7, 47.8, 47.9, 48. , 48.1, 48.2, 48.3, 48.4, 48.5,
48.6, 48.7, 48.8, 48.9, 49. , 49.1, 49.2, 49.3, 49.4,
49.5, 49.6, 49.7, 49.8, 49.9, -50. , -49.9, -49.8, -49.7,
-49.6, -49.5, -49.4, -49.3, -49.2, -49.1, -49. , -48.9, -48.8,
-48.7, -48.6, -48.5, -48.4, -48.3, -48.2, -48.1, -48. , -47.9,
-47.8, -47.7, -47.6, -47.5, -47.4, -47.3, -47.2, -47.1, -47. ,
-46.9, -46.8, -46.7, -46.6, -46.5, -46.4, -46.3, -46.2, -46.1,
...
-3.7, -3.6, -3.5, -3.4, -3.3, -3.2, -3.1, -3. , -2.9,
-2.8, -2.7, -2.6, -2.5, -2.4, -2.3, -2.2, -2.1, -2. ,
-1.9, -1.8, -1.7, -1.6, -1.5, -1.4, -1.3, -1.2, -1.1,
-1. , -0.9, -0.8, -0.7, -0.6, -0.5, -0.4, -0.3, -0.2,
-0.1])
从其频率值xfp可以看出来,其变化是0Hz->50Hz->-50Hz->0Hz
那我们只要0-50Hz的频率该怎么做,有两种办法
方法1
通过plt.xlim(x1, x2) #x1, x2是要展示出来的坐标值
ax1 = plt.subplot(1, 2, 2)
plt.plot(xfp, xf) # 画fft图像
plt.xlabel('f(Hz)')
plt.ylabel('Amp')
plt.title('y=sin(2*π*2*t)p fft图')
plt.xlim(0, int(fs/2)) #展示频率在(0,int(fs/2))范围内的图像
输出结果

方法2
只取正频率,即取前半个长度的点数
xf = np.fft.fft(y) # 对离散数据y做fft变换得到变换之后的数据xf
xf = abs(xf) # 将复数求模
xf = xf[0:int(len(xf)/2)] #取xf前半个长度
xfp = np.fft.fftfreq(len(y), d=1 / fs) # fftfreq(length,fs),计算得到频率
xfp = xfp[0:int(len(xfp)/2)] #取xfp前半个长度
ax1 = plt.subplot(1, 2, 2)
plt.plot(xfp, xf) # 画fft图像
plt.xlabel('f(Hz)')
plt.ylabel('Amp')
plt.title('y=sin(2*π*2*t)p fft图')
输出结果

采样定理
还记得第一张图,采样频率为10Hz时,其形状比较尖锐,那做fft是否也能分析出信号频率呢?
答案是可以的。采样定理是这样说的:采样频率需至少为所关心频率的2倍时,才能保留所关心信号的信息。采样10Hz是信号频率2Hz的5倍,大于2倍,所以是可以分析出来的
现在对采样频率为10Hz在的信号进行fft分析
####----进行fft---####
matplotlib.rcParams['axes.unicode_minus']=False #用来正常显示正负号
t = np.linspace(start=0, stop=10, num=100) # 采样频率fs=1000÷10=10
y = 4*np.sin(2*np.pi*t*2) # y=sin(2*π*f*t) # 这里f=2
# 画时域图
ax1 = plt.subplot(1, 2, 1)
plt.plot(t, y)
plt.xlabel('t(s)')
plt.ylabel('f(Hz)')
plt.title('y=sin(2*π*2*t) 时域图')
# 画fft图
fs = 10 # 采样频率
xf = np.fft.fft(y) # 对离散数据y做fft变换得到变换之后的数据xf
xfp = np.fft.fftfreq(len(y), d=1 / fs) # fftfreq(length,fs),计算得到频率
xf = abs(xf) # 将复数求模
ax1 = plt.subplot(1, 2, 2)
plt.plot(xfp, xf) # 画fft图像
plt.xlim(0, int(fs/2))
plt.xlabel('f(Hz)')
plt.ylabel('Amp')
plt.title('y=sin(2*π*2*t)p fft图')
结果
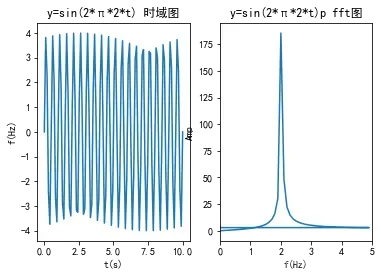
由图可知,当采样频率比较低时,其在频率为2Hz附近也会存在幅值比较低的频率,这种现象叫频谱泄露。
参考资料
信号处理 | 傅里叶变换、短时傅里叶变换、小波变换、希尔伯特变换、希尔伯特黄变换
一幅图弄清DFT与DTFT,DFS的关系
如何 FFT(快速傅里叶变换) 求幅度、频率(超详细 含推导过程)
DSP基本名词术语及其关系
信号处理若干名词解释(I)
信号处理若干名词解释(II)
什么是泄漏?
什么是混叠
什么是窗函数
plt.subplot()使用方法以及参数介绍
解决Matplotlib绘图中,负号不正常显示问题
欢迎关注我的公众号:
CWRU数据集介绍
论文学习-A Deep Learning Method for Bearing Fault Diagnosis Based on Time-frequency Image
论文?专利?科研?就业?研二学长带着满满干货分享入门知识啦
数据集 | 很全的轴承与齿轮数据集下载网站整理
论文学习|第2篇-综述:机器学习在机器故障诊断中的应用: 回顾和路线图
文章出处登录后可见!
