Binaryfloating pointmath 是这样的。在大多数编程语言中，它基于 IEEE 754 标准。问题的症结在于，数字以这种格式表示为整数乘以 2 的幂。分母不是2的幂的有理数（如0.1，即1/10）不能精确表示。

对于0.1在标准binary64格式中，表示可以完全写为

• 0.1000000000000000055511151231257827021181583404541015625 in decimal, or
• 0x1.999999999999ap-4 in C99 hexfloat notation .

相反，有理数0.1，即1/10，可以完全写成

• 0.1 in decimal, or
• 0x1.99999999999999…p-4 in an analogue of C99 hexfloat notation, where the … represents an unending sequence of 9’s.

程序中的常量0.2和0.3也将近似于它们的真实值。恰好最接近doubleto0.2大于有理数0.2但最接近doubleto0.3小于有理数0.3。 0.1和0.2之和最终大于有理数0.3，因此与代码中的常数不一致。

浮点算术问题的一个相当全面的处理是每个计算机科学家都应该知道的关于浮点算术的知识。有关更容易理解的解释，请参阅floating-point-gui.de。

旁注：所有位置（base-N）数字系统都精确地共享这个问题

普通的旧十进制（以 10 为底）数字也有同样的问题，这就是为什么像 1/3 这样的数字最终会变成 0.333333333…

您刚刚偶然发现了一个数字（3/10），它恰好很容易用十进制系统表示，但不适合二进制系统。它也是双向的（在某种程度上）：1/16是十进制的丑数（0.0625），但在二进制中，它看起来就像十进制的万分之一（0.0001）** – 如果我们在日常生活中习惯使用以 2 为底的数字系统，你甚至会看到这个数字，并本能地理解你可以通过减半、一次又一次、一次又一次地减半来到达那里。

** 当然，浮点数在内存中的存储方式并不完全正确（它们使用一种科学记数法）。然而，它确实说明了二进制浮点精度错误往往会出现这一点，因为我们通常感兴趣的“现实世界”数字通常是十的幂 – 但仅仅是因为我们使用十进制数字系统 -今天。这也是为什么我们会说 71% 而不是“每 7 个中有 5 个”之类的东西（71% 是一个近似值，因为 5/7 不能用任何十进制数精确表示）。

所以不：二进制浮点数没有被破坏，它们只是碰巧和其他所有基于 N 的数字系统一样不完美:)

旁注：在编程中使用浮点数

在实践中，这个精度问题意味着您需要使用舍入函数将浮点数四舍五入到您感兴趣的小数位，然后再显示它们。

您还需要用允许一定容差的比较替换相等测试，这意味着：

不要做if (x == y) { ... }

而是做if (abs(x - y) < myToleranceValue) { ... }。

其中abs是绝对值。myToleranceValue需要为您的特定应用选择 – 这与您准备允许多少“摆动空间”以及您将要比较的最大数字有很大关系是（由于精度问题的损失）。请注意您选择的语言中的“epsilon”样式常量。这些不得用作公差值。

它的破坏方式与您在小学时学到的十进制（以 10 为基数）符号的破坏方式完全相同，仅针对以 2 为基础的符号。

要理解，想想把 1/3 表示为十进制值。不可能做到完全正确！同样，1/10（十进制 0.1）不能以 2 进制（二进制）精确表示为“十进制”值；小数点后的重复模式永远存在。该值不精确，因此您无法使用普通浮点方法对其进行精确数学运算。

硬件设计师的观点

我相信我应该为此添加硬件设计师的观点，因为我设计和构建了浮点硬件。了解错误的来源可能有助于理解软件中发生的事情，最终，我希望这有助于解释浮点错误发生的原因，并且似乎随着时间的推移而累积。

一、概述

从工程的角度来看，大多数浮点运算都会有一些错误，因为进行浮点计算的硬件只需要在最后一个单位的误差小于一半。因此，许多硬件将停止在一个精度上，该精度只需要在单个操作的最后一个位置产生小于一半的误差，这在浮点除法中尤其成问题。什么构成单个操作取决于该单元需要多少个操作数。大多数情况下，它是两个，但有些单元需要 3 个或更多操作数。因此，不能保证重复的操作会导致理想的错误，因为错误会随着时间的推移而累积。

2. 标准

大多数处理器遵循 IEEE-754 标准，但有些使用非规范化或不同的标准。例如，IEEE-754 中有一种非规范化模式，它允许以牺牲精度为代价来表示非常小的浮点数。然而，下面将介绍 IEEE-754 的标准化模式，这是典型的操作模式。

在 IEEE-754 标准中，允许硬件设计人员使用任何 error/epsilon 值，只要它小于最后一个单位的二分之一，并且结果只需小于最后一个单位的二分之一一个操作的地方。这解释了为什么当有重复操作时，错误加起来。对于 IEEE-754 双精度，这是第 54 位，因为 53 位用于表示数字部分（归一化），也称为尾数, 的浮点数（例如。5.3e5 中的 5.3）。接下来的部分将更详细地介绍各种浮点运算导致硬件错误的原因。

三、除法舍入误差的原因

浮点除法错误的主要原因是用于计算商的除法算法。大多数计算机系统计算除法使用乘以逆，主要在Z=X/Y，Z = X * (1/Y)。一个除法是迭代计算的，即。每个循环计算一些位商直到达到所需的精度，对于 IEEE-754 来说，它是最后一位误差小于一个单位的任何东西。Y (1/Y) 的倒数表称为商选择表 (QST)在慢除法中，商选择表的位大小通常是基数的宽度，或者每次迭代计算的商的位数，加上一些保护位。对于 IEEE-754 标准，双精度（64 位），它将是除法器的基数的大小，加上一些保护位 k，其中k>=2。例如，一个典型的除法器商选择表计算 2 位的商在 a时间（基数 4）将是2+2= 4位（加上一些可选位）。

3.1 Division Rounding Error: Approximation of Reciprocal

商选择表中的倒数取决于除法：慢除法如 SRT 除法，或快速除法如 Goldschmidt 除法；每个条目都根据除法算法进行修改，以尝试产生尽可能低的误差。但是，无论如何，所有倒数都是实际倒数的近似值，并引入了一些误差元素。慢除法和快速除法方法都迭代计算商，即每一步计算商的一些位数，然后从被除数中减去结果，除法器重复这些步骤，直到误差小于最后一个单位的一半。慢除法计算一个每个步骤中商的位数固定，构建成本通常较低，而快速除法方法计算每个步骤的可变位数，构建成本通常更高。除法方法最重要的部分是大多数它们依赖于倒数的近似值的重复乘法，因此它们容易出错。

4. 其他运算中的舍入误差：截断

所有操作中舍入误差的另一个原因是 IEEE-754 允许的最终答案截断的不同模式。有截断、向零舍入、最近舍入（默认）、向下舍入和向上舍入。所有方法都会在单个操作的最后一个位置引入小于一个单位的误差元素。随着时间的推移和重复的操作，截断也会累积地增加结果错误。这种截断误差在求幂中尤其成问题，它涉及某种形式的重复乘法。

5.重复操作

由于进行浮点计算的硬件只需要在单个操作的最后一个位置产生一个误差小于一半的结果，如果不注意，误差会随着重复操作而增长。这就是为什么在需要有界误差的计算中，数学家使用诸如在 IEEE-754 的最后一个位置使用四舍五入到最近的偶数等方法，因为随着时间的推移，错误更有可能相互抵消，和区间算术结合IEEE 754舍入模式的变化来预测舍入误差，并纠正它们。由于与其他舍入模式相比，它的相对误差较低，舍入到最接近的偶数（在最后一位）是 IEEE-754 的默认舍入模式。

请注意，默认的舍入模式，最后一位舍入到最近的偶数位，保证一次操作的最后一位错误小于一个单位的二分之一。单独使用截断、向上舍入和向下舍入可能会导致错误大于最后一位单位的二分之一，但小于最后一位单位，因此不建议使用这些模式，除非它们是用于区间算术。

6.总结

简而言之，浮点运算出错的根本原因是硬件截断和除法倒数截断的结合。由于 IEEE-754 标准只要求单次运算的最后一位误差小于一个单位的二分之一，因此重复运算的浮点误差会累加起来，除非得到纠正。

这里的大多数答案都用非常枯燥的技术术语来解决这个问题。我想用普通人可以理解的方式来解决这个问题。

想象一下，您正在尝试切比萨饼。你有一个机器人披萨刀，可以将披萨片切成两半。它可以将整个披萨减半，也可以将现有切片减半，但无论如何，减半总是准确的。

那个比萨刀的动作非常精细，如果你从一个完整的比萨开始，然后把它减半，然后每次将最小的切片继续减半，你可以减半 53 次，以免切片太小而无法达到高精度的能力。那时，您不能再将那个非常薄的切片减半，而必须按原样包含或排除它。

现在，您将如何将所有切片以这样一种方式拼凑起来，加起来相当于披萨的十分之一 (0.1) 或五分之一 (0.2)？认真考虑一下，然后尝试解决。你甚至可以尝试使用真正的比萨，如果你手头有一个神话般的精密比萨刀。:-)

当然，大多数有经验的程序员都知道真正的答案，那就是，无论切片多么精细，都无法将披萨的十分之一或五分之一拼凑在一起。你可以做一个很好的近似，如果将 0.1 的近似值与 0.2 的近似值相加，得到一个相当好的近似值 0.3，但它仍然只是一个近似值。

对于双精度数（这是允许您将减半你的披萨53倍精度），立即较少的数量和大于0.1的0.09999999999999999167332731531132594682276248931884765625和0.1000000000000000055511151231257827021181583404541015625.The后者是颇有几分接近0.1比前者，所以数字给定输入 0.1，解析器将支持后者。

（这两个数字之间的差异是“最小切片”，我们必须决定要么包括，它会引入向上偏差，要么排除，它会引入向下偏差。最小切片的技术术语是 anulp。）

在 0.2 的情况下，数字都是一样的，只是放大了 2 倍。再次，我们赞成略高于 0.2 的值。

请注意，在这两种情况下，0.1 和 0.2 的近似值都有轻微的向上偏差。如果我们添加足够多的这些偏差，它们会使数字越来越远离我们想要的，事实上，在 0.1 的情况下+ 0.2，偏差足够大，结果数字不再是最接近 0.3 的数字。

特别地，0.1 + 0.2是真的0.1000000000000000055511151231257827021181583404541015625 + 0.200000000000000011102230246251565404236316680908203125 = 0.3000000000000000444089209850062616169452667236328125，而最接近0.3数量实际上是0.299999999999999988897769753748434595763683319091796875。

P.S。Some programming languages also provide pizza cutters that cansplit slices into exact tenths。Although such pizza cutters are uncommon, if you do have access to one, you should use it when it’s important to be able to get exactly one-tenth or one-fifth of a slice.

（最初发布在 Quora 上。）

我的答案很长，所以我把它分成三个部分。由于问题是关于浮点数学的，所以我把重点放在了机器的实际作用上。我还专门针对双精度（64 位）精度，但该参数同样适用于任何浮点运算。

前言

一个 IEEE 754 双精度二进制浮点格式 (binary64) 数字表示形式的数字

值 = (-1)^s * (1.m51m50…m2m1m0)2* 2e-1023

64位：

• 第一位是符号位：如果数字是负数，则为 1，否则为 0
  1
  .
• 接下来的 11 位是指数，偏移了 1023。换句话说，从双精度数中读取指数位后，必须减去 1023 才能获得 2 的幂。
• 剩下的 52 位是有效数（或尾数）。在尾数中，“隐含” 1. 总是
  2
  省略，因为任何二进制值的最高有效位都是 1 。

1- IEEE 754 允许分配零的概念-+0和-0被区别对待：1 / (+0)是正无穷大；1 / (-0)是负无穷大。对于零值，尾数和指数位都为零。注意：零值（+0 和 -0）明确不归类为 denormal2。

2- 非正规数不是这种情况，它的偏移指数为零（和隐含的0.）。非正规双精度数的范围是 dmin≤ |x| ≤ dmax，其中 dmin（可表示的最小非零数）为 2-1023 – 51（≈ 4.94 * 10-324），dmax（最大非正规数，其尾数完全由1s组成）为 2-1023 + 1 – 2-1023 – 51（≈ 2.225 * 10-308）。

将双精度数转换为二进制

存在许多在线转换器将双精度浮点数转换为二进制（例如。atbinaryconvert.com），但这里有一些示例 C# 代码来获得双精度数的 IEEE 754 表示（我用冒号分隔三个部分（: ):

public static string BinaryRepresentation(double value)
{
    long valueInLongType = BitConverter.DoubleToInt64Bits(value);
    string bits = Convert.ToString(valueInLongType, 2);
    string leadingZeros = new string('0', 64 - bits.Length);
    string binaryRepresentation = leadingZeros + bits;

    string sign = binaryRepresentation[0].ToString();
    string exponent = binaryRepresentation.Substring(1, 11);
    string mantissa = binaryRepresentation.Substring(12);

    return string.Format("{0}:{1}:{2}", sign, exponent, mantissa);
}

切入正题：原始问题

（TL；DR版本跳到底部）

卡托约翰斯顿（提问者）问为什么 0.1 + 0.2 != 0.3。

用二进制编写（用冒号分隔三部分），值的 IEEE 754 表示为：

0.1 => 0:01111111011:1001100110011001100110011001100110011001100110011010
0.2 => 0:01111111100:1001100110011001100110011001100110011001100110011010

请注意，尾数由重复的0011数字组成。这就是为什么计算会出现任何错误的关键——0.1、0.2和0.3不能用二进制精确地表示为二进制位的有限个数，不超过1/9、1/3或1/ 7 可以精确地表示小数位数。

另请注意，我们可以将指数中的幂减少 52 并将二进制表示中的点向右移动 52 位（很像 10-3* 1.23 == 10-5* 123）。这使我们能够表示二进制表示为它以 a * 2p 形式表示的精确值。其中 ‘a’ 是一个整数。

将指数转换为十进制，去除偏移量，并重新添加隐含的1（在方括号中），0.1 和 0.2 是：

0.1 => 2^-4 * [1].1001100110011001100110011001100110011001100110011010
0.2 => 2^-3 * [1].1001100110011001100110011001100110011001100110011010
or
0.1 => 2^-56 * 7205759403792794 = 0.1000000000000000055511151231257827021181583404541015625
0.2 => 2^-55 * 7205759403792794 = 0.200000000000000011102230246251565404236316680908203125

要添加两个数字，指数需要相同，即：

0.1 => 2^-3 *  0.1100110011001100110011001100110011001100110011001101(0)
0.2 => 2^-3 *  1.1001100110011001100110011001100110011001100110011010
sum =  2^-3 * 10.0110011001100110011001100110011001100110011001100111
or
0.1 => 2^-55 * 3602879701896397  = 0.1000000000000000055511151231257827021181583404541015625
0.2 => 2^-55 * 7205759403792794  = 0.200000000000000011102230246251565404236316680908203125
sum =  2^-55 * 10808639105689191 = 0.3000000000000000166533453693773481063544750213623046875

由于和不是 2n* 1.{bbb} 的形式，我们将指数加一并移动小数点（二进制）得到：

sum = 2^-2  * 1.0011001100110011001100110011001100110011001100110011(1)
    = 2^-54 * 5404319552844595.5 = 0.3000000000000000166533453693773481063544750213623046875

现在尾数有 53 位（第 53 位在上一行的方括号中）。IEEE 754 的默认舍入模式是“舍入到最近” – 即。如果一个数字 x 落在两个值 a 和 b 之间，则最低有效位的值是选择零。

a = 2^-54 * 5404319552844595 = 0.299999999999999988897769753748434595763683319091796875
  = 2^-2  * 1.0011001100110011001100110011001100110011001100110011

x = 2^-2  * 1.0011001100110011001100110011001100110011001100110011(1)

b = 2^-2  * 1.0011001100110011001100110011001100110011001100110100
  = 2^-54 * 5404319552844596 = 0.3000000000000000444089209850062616169452667236328125

注意a和b仅在最后一位不同；...0011+1=...0100。在这种情况下，最低有效位为零的值是 b，所以总和是：

sum = 2^-2  * 1.0011001100110011001100110011001100110011001100110100
    = 2^-54 * 5404319552844596 = 0.3000000000000000444089209850062616169452667236328125

而 0.3 的二进制表示是：

0.3 => 2^-2  * 1.0011001100110011001100110011001100110011001100110011
    =  2^-54 * 5404319552844595 = 0.299999999999999988897769753748434595763683319091796875

它与 0.1 和 0.2 之和的二进制表示仅相差 2-54。

0.1 和 0.2 的二进制表示是 IEEE 754 允许的数字的最准确表示。由于默认的舍入模式，添加这些表示会产生一个仅在最低有效位上有所不同的值。

TL;博士

以 IEEE 754 二进制表示形式写0.1 + 0.2（用冒号分隔三部分）并将其与0.3进行比较，这是（我已将不同的位放在方括号中）：

0.1 + 0.2 => 0:01111111101:0011001100110011001100110011001100110011001100110[100]
0.3       => 0:01111111101:0011001100110011001100110011001100110011001100110[011]

转换回十进制，这些值是：

0.1 + 0.2 => 0.300000000000000044408920985006...
0.3       => 0.299999999999999988897769753748...

与原始值相比，差异正好是 2-54，即 ~5.5511151231258 × 10-17- 微不足道（对于许多应用程序）。

比较浮点数的最后几位本质上是危险的，因为任何阅读了著名的“每个计算机科学家应该知道的关于浮点算术的知识”（涵盖了这个答案的所有主要部分）的人都会知道。

大多数计算器使用额外的保护数字来解决这个问题，这就是0.1 + 0.2会给出0.3：最后几位被四舍五入。

简而言之，因为：

浮点数不能用二进制精确表示所有小数

所以就像 10/3 不精确地以 10 为底（它将是 3.33..。重复），以同样的方式 1/10 在二进制中不存在。

所以呢？如何处理？有什么解决方法吗？

为了提供最好的解决方案我可以说我发现了以下方法：

parseFloat((0.1 + 0.2).toFixed(10)) => Will return 0.3

让我解释一下为什么它是最好的解决方案。正如上面提到的其他人回答的那样，使用现成的 Javascript toFixed() 函数来解决问题是一个好主意。但很可能你会遇到一些问题。

想象一下，您要将两个浮点数相加，例如0.2和0.7这里是：0.2 + 0.7 = 0.8999999999999999。

您的预期结果是0.9这意味着在这种情况下您需要一个精度为 1 位的结果。所以您应该使用(0.2 + 0.7).tofixed(1)但您不能只给 toFixed() 提供某个参数，因为它取决于给定的数字，例如

0.22 + 0.7 = 0.9199999999999999

在此示例中，您需要 2 位精度，所以它应该是toFixed(2)，那么适合每个给定浮点数的参数应该是什么？

您可能会说在每种情况下都设为 10：

(0.2 + 0.7).toFixed(10) => Result will be "0.9000000000"

该死！您将如何处理 9 之后那些不需要的零？现在是时候将其转换为浮点数以使其符合您的要求：

parseFloat((0.2 + 0.7).toFixed(10)) => Result will be 0.9

现在您找到了解决方案，最好将它作为这样的函数提供：

function floatify(number){
           return parseFloat((number).toFixed(10));
        }
    

让我们自己尝试一下：

function floatify(number){
       return parseFloat((number).toFixed(10));
    }
 
function addUp(){
  var number1 = +$("#number1").val();
  var number2 = +$("#number2").val();
  var unexpectedResult = number1 + number2;
  var expectedResult = floatify(number1 + number2);
  $("#unexpectedResult").text(unexpectedResult);
  $("#expectedResult").text(expectedResult);
}
addUp();

input{
  width: 50px;
}
#expectedResult{
color: green;
}
#unexpectedResult{
color: red;
}

<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script>
<input id="number1" value="0.2" onclick="addUp()" onkeyup="addUp()"/> +
<input id="number2" value="0.7" onclick="addUp()" onkeyup="addUp()"/> =
<p>Expected Result: <span id="expectedResult"></span></p>
<p>Unexpected Result: <span id="unexpectedResult"></span></p>

你可以这样使用它：

var x = 0.2 + 0.7;
floatify(x);  => Result: 0.9

AsW3SCHOOLSssuggests 还有另一种解决方案，您可以乘除以解决上述问题：

var x = (0.2 * 10 + 0.1 * 10) / 10;       // x will be 0.3

请记住，(0.2 + 0.1) * 10 / 10虽然看起来一样，但根本不起作用！我更喜欢第一个解决方案，因为我可以将它用作将输入浮点数转换为准确输出浮点数的函数。

除了其他正确答案之外，您可能需要考虑缩放值以避免浮点运算问题。

例如：

var result = 1.0 + 2.0;     // result === 3.0 returns true

… 代替：

var result = 0.1 + 0.2;     // result === 0.3 returns false

表达式0.1 + 0.2 === 0.3在 JavaScript 中返回false，但幸运的是浮点中的整数运算是精确的，因此可以通过缩放来避免十进制表示错误。

作为一个实际示例，为避免精度至关重要的浮点问题，建议 1 将货币处理为表示美分数量的整数：2550美分而不是25.50美元。

1Douglas Crockford：JavaScript：好的部分：附录 A – 糟糕的部分（第 105 页）。

浮点舍入误差。由于缺少 5 的素数因子，0.1 在 base-2 中不能像在 base-10 中那样准确地表示。就像 1/3 需要无限位数来表示十进制，但是是“0.1”在 base-3 中，0.1 在 base-2 中具有无限位数，而在 base-10 中则没有。并且计算机没有无限量的内存。

存储在计算机中的浮点数由两部分组成，一个整数和一个指数，以指数为底并乘以整数部分。

如果计算机在 10 进制下工作，0.1将是1 x 10⁻¹，0.2将是2 x 10⁻¹，0.3将是3 x 10⁻¹。整数数学既简单又精确，所以加0.1 + 0.2显然会得到0.3。

计算机通常不以 10 为底工作，它们以 2 为底工作。您仍然可以获得某些值的精确结果，例如0.5is1 x 2⁻¹和0.25is1 x 2⁻²，并将它们相加得到3 x 2⁻²或0.75。确切地。

问题在于数字可以精确地以 10 为底，但不能以 2 为底。这些数字需要四舍五入到最接近的等值。假设很常见的IEEE 64位浮点格式，离0.1最接近的数是3602879701896397 x 2⁻⁵⁵，离0.2最接近的数是7205759403792794 x 2⁻⁵⁵；将它们加在一起得到10808639105689191 x 2⁻⁵⁵，或精确的十进制值0.3000000000000000444089209850062616169452667236328125。浮点数通常四舍五入以便显示。

浮点数的陷阱是它们看起来像十进制，但它们以二进制工作。

2 的唯一质因数是 2，而 10 的质因数是 2 和 5。结果是每个可以精确写为二进制分数的数字也可以精确写为十进制分数，但只有可以写成十进制分数的数字可以写成二进制分数。

浮点数本质上是具有有限有效数字的二进制分数。如果超过这些有效数字，则结果将四舍五入。

当您在代码中键入文字或调用函数将浮点数解析为字符串时，它需要一个十进制数，并将该十进制数的二进制近似值存储在变量中。

当您打印浮点数或调用函数以将其转换为字符串时，它会打印浮点数的十进制近似值。可以将二进制数精确地转换为十进制数，但在转换为字符串* 时，我所知道的任何语言默认情况下都不会这样做。一些语言使用固定数量的有效数字，其他语言使用最短的字符串“往返”回到相同的浮点值。

* Python确实在将浮点数转换为“decimal.Decimal”时进行精确转换。这是我所知道的获得浮点数的精确十进制等值的最简单方法。

不，没有损坏，但大多数小数必须近似

概括

不幸的是，浮点算术精确，它与我们通常的以 10 为底的数字表示不匹配，所以事实证明，我们经常给它输入与我们编写的内容略有不同的输入。

即使是简单的数字，如 0.01, 0.02, 0.03, 0.04 …。0.24 不能完全表示为二进制分数。如果你数 0.01, .02, .03 …, 直到你得到 0.25 你才会得到第一个分数可在 base2 中表示。如果您尝试使用 FP，您的 0.01 会稍微偏离，因此将其中的 25 个添加到精确的 0.25 的唯一方法将需要涉及保护位和舍入的一长串因果关系。这很难预测所以我们举起手说“FP 不准确”，但这不是真的。

我们不断地为 FP 硬件提供一些以 10 为底的看似简单但以 2 为底的重复分数。

这怎么发生的？

当我们用十进制写时，每个分数（特别是每个终止小数）都是形式的有理数

一个 / (2nx 5m)

在二进制中，我们只得到了 2nterm，即：

一个/2n

所以在十进制中，我们不能表示 1/3。因为以 10 为底包含 2 作为质因数，所以我们可以写成二进制小数的每个数字也可以写成以 10 为底的分数。但是，我们写成以 10 为底的分数几乎是不可表示的二进制。在 0.01, 0.02, 0.03 ..的范围内。0.99，我们的 FP 格式只能表示三个数字：0.25, 0.50, 和 0.75，因为它们是 1/4, 1/2, 和 3/4，所有仅使用 2nterm 的素数。

在 base10 中我们不能表示 1/3。但在二进制中，我们不能做 1/10 或 1/3。

因此，虽然每个二进制分数都可以写成十进制，但反之则不然。事实上，大多数小数部分都以二进制形式重复。

处理它

开发人员通常被指示做< epsilon比较，更好的建议可能是四舍五入到整数值（在C库中：round()和roundf()，即保持FP格式）然后比较。四舍五入到特定的小数长度解决了大多数输出​​问题。

此外，在实数运算问题（FP 是在早期的、非常昂贵的计算机上发明的问题）中，宇宙的物理常数和所有其他测量只有相对少量的有效数字知道，所以整个问题空间无论如何是“不精确的”。 FP“准确性”在这种应用程序中不是问题。

当人们尝试使用 FP 进行豆子计数时，整个问题就真正出现了。它确实可以解决这个问题，但前提是你坚持使用整数值，这会破坏使用它的意义。这就是为什么我们拥有所有这些小数部分软件图书馆。

我喜欢克里斯的比萨回答，因为它描述了实际问题，而不仅仅是关于“不准确”的通常挥手致意。如果 FP 只是“不准确”，我们可以解决这个问题，并且在几十年前就可以做到。我们没有这样做的原因是因为 FP 格式紧凑且快速，它是处理大量数字的最佳方式。此外，它是太空时代和军备竞赛以及早期尝试使用小内存系统解决非常慢的计算机的大问题的遗产。 （有时，单个磁芯用于 1 位存储，但那是另一回事。）

结论

如果您只是在银行数豆子，那么首先使用十进制字符串表示的软件解决方案效果很好。但是你不能那样做量子色动力学或空气动力学。

浮点数在硬件级别表示为二进制数的分数（以 2 为基数）。例如小数部分：

0.125

具有值 1/10 + 2/100 + 5/1000 并且以同样的方式具有二进制分数：

0.001

值为 0/2 + 0/4 + 1/8。这两个分数具有相同的值，唯一的区别是第一个是十进制分数，第二个是二进制分数。

不幸的是，大多数十进制分数不能以二进制分数精确表示。因此，一般情况下，您给出的浮点数仅近似为要存储在机器中的二进制分数。

以 10 为底的问题更容易解决。例如，分数 1/3。您可以将其近似为小数：

0.3

或更好，

0.33

或更好，

0.333

等等。不管你写了多少个小数位，结果永远不会正好是 1/3，但它是一个总是更接近的估计值。

同样，无论您使用多少个以 2 为底的小数位，十进制值 0.1 都不能完全表示为二进制分数。在以 2 为底的情况下，1/10 是以下周期数：

0.0001100110011001100110011001100110011001100110011 ...

停在任何有限数量的位上，你会得到一个近似值。

对于 Python，在典型的机器上，浮点数的精度使用 53 位，因此输入十进制 0.1 时存储的值是二进制小数。

0.00011001100110011001100110011001100110011001100110011010

接近但不完全等于 1/10。

由于浮点数在解释器中的显示方式，很容易忘记存储的值是原始十进制小数的近似值。Python 仅显示以二进制形式存储的值的十进制近似值。如果 Python 要输出真正的十进制值为 0.1 存储的二进制近似值，它将输出：

>>> 0.1
0.1000000000000000055511151231257827021181583404541015625

这比大多数人预期的要多得多，因此 Python 显示一个四舍五入的值以提高可读性：

>>> 0.1
0.1

重要的是要理解这实际上是一种错觉：存储的值并不完全是 1/10，只是在显示屏上存储的值被四舍五入。一旦您使用这些值执行算术运算，这一点就会变得很明显：

>>> 0.1 + 0.2
0.30000000000000004

这种行为是机器浮点表示的本质所固有的：它不是 Python 中的错误，也不是代码中的错误。您可以在使用硬件支持计算浮点数的所有其他语言中观察到相同类型的行为（尽管某些语言默认情况下不会使差异可见，或者并非在所有显示模式下都可见）。

另一个惊喜是这个固有的。例如，如果您尝试将值 2.675 舍入到小数点后两位，您将得到

>>> round (2.675, 2)
2.67

round() 原语的文档表明它四舍五入到离零最近的值。由于小数部分正好在 2.67 和 2.68 之间，你应该期望得到 2.68（二进制近似值）。情况并非如此，但是，因为当小数 2.675 转换为浮点数时，它是通过一个近似值存储的，其精确值为：

2.67499999999999982236431605997495353221893310546875

由于近似值比 2.68 略接近 2.67，因此舍入向下。

如果您处于将十进制数字舍入一半很重要的情况，您应该使用十进制模块。顺便说一下，十进制模块还提供了一种方便的方法来“查看”为任何浮点数存储的确切值。

>>> from decimal import Decimal
>>> Decimal (2.675)
>>> Decimal ('2.67499999999999982236431605997495353221893310546875')

0.1 不完全存储在 1/10 中的另一个后果是 0.1 的十个值的总和也不给出 1.0：

>>> sum = 0.0
>>> for i in range (10):
... sum + = 0.1
...>>> sum
0.9999999999999999

二进制浮点数的算术具有许多这样的惊喜。“0.1”的问题在下面的“表示错误”部分中详细解释。有关这些惊喜的更完整列表，请参阅浮点的危险。

确实没有简单的答案，但是不要过分怀疑浮动虚拟数！在 Python 中，浮点数运算中的错误是由底层硬件引起的，并且在大多数机器上，每次操作的错误率不超过 2 ** 53。这对于大多数任务来说是非常必要的，但您应该记住，这些不是十进制运算，并且对浮点数的每个运算都可能会遇到新的错误。

尽管存在病态的情况，但对于大多数常见的用例，您将在最后通过简单地四舍五入到您想要的显示小数位数获得预期的结果。有关如何精细控制浮点数的显示，请参阅字符串格式语法str.format() 方法的格式规范。

这部分答案详细解释了“0.1”的例子，并展示了如何自己对这种情况进行精确分析。我们假设您熟悉浮点数的二进制表示。术语表示错误意味着大多数小数部分不能以二进制精确表示。这是 Python（或 Perl、C、C++、Java、Fortran 和许多其他）通常不以十进制显示精确结果的主要原因：

>>> 0.1 + 0.2
0.30000000000000004

为什么 ？ 1/10 和 2/10 不能用二进制分数精确表示。但是，今天（2010 年 7 月）的所有机器都遵循 IEEE-754 浮点数算术标准。大多数平台使用“IEEE-754 双精度”表示 Python 浮点数。双精度 IEEE-754 使用 53 位精度，因此在读取计算机时尝试将 0.1 转换为 J / 2 ** N 形式的最接近的小数，其中 J 是正好 53 位的整数。重写：

1/10 ~ = J / (2 ** N)

在 ：

J ~ = 2 ** N / 10

记住 J 正好是 53 位（所以> = 2 ** 52 但 <2 ** 53），N 的最佳可能值是 56：

>>> 2 ** 52
4503599627370496
>>> 2 ** 53
9007199254740992
>>> 2 ** 56/10
7205759403792793

所以 56 是 N 的唯一可能值，它正好为 J 留下 53 位。因此，J 的最佳可能值是这个商，四舍五入：

>>> q, r = divmod (2 ** 56, 10)
>>> r
6

由于进位大于 10 的一半，通过四舍五入获得最佳近似值：

>>> q + 1
7205759403792794

因此，“IEEE-754 双精度”中 1/10 的最佳近似值是高于 2 ** 56，即：

7205759403792794/72057594037927936

请注意，由于向上舍入，结果实际上略大于 1/10；如果我们没有四舍五入，商将略小于 1/10。但在任何情况下都不完全是 1/10！

所以计算机永远不会“看到”1/10：它看到的是上面给出的确切分数，使用“IEEE-754”中的双精度浮点数的最佳近似值：

>>>. 1 * 2 ** 56
7205759403792794.0

如果我们将这个分数乘以 10 ** 30，我们可以观察到它的小数点后 30 位的强权值。

>>> 7205759403792794 * 10 ** 30 // 2 ** 56
100000000000000005551115123125L

意味着存储在计算机中的确切值大约等于十进制值 0.100000000000000005551115123125。在 Python 2.7 和 Python 3.1 之前的版本中，Python 将这些值四舍五入到 17 个有效小数位，显示“0.10000000000000001”。在当前版本的 Python ，显示的值是小数部分尽可能短的值，同时在转换回二进制时给出完全相同的表示，仅显示“0.1”。

浮点舍入误差。来自每个计算机科学家都应该知道的关于浮点运算的知识：

将无限多个实数压缩为有限位数需要近似表示。尽管整数有无限多，但在大多数程序中，整数计算的结果可以存储在 32 位中。相反，给定任何固定位数，大多数实数计算将产生无法使用那么多位精确表示的量。因此，浮点计算的结果必须经常四舍五入以适应其有限表示。这种舍入误差是浮点计算的特征。

鉴于没有人提到这…

一些高级语言（例如 Python 和 Java）带有克服二进制浮点限制的工具。例如：

• Python 的十进制模块和 Java 的 BigDecimal 类，它们在内部用十进制表示法（与二进制表示法相反）表示数字。两者都具有有限的精度，因此它们仍然容易出错，但是它们解决了二进制浮点运算的大多数常见问题。
  处理金钱时，小数非常好：10 美分加 20 美分总是正好是 30 美分：>>> 0.1 + 0.2 == 0.3False>>> Decimal(‘0.1’) + Decimal(‘0.2’) == Decimal( ‘0.3’) 真
  Python 的十进制模块基于 IEEE 标准 854-1987 。
• Python 的分数模块和 Apache Common 的 BigFraction 类。两者都将有理数表示为（分子，分母）对，并且它们可能比十进制浮点算术提供更准确的结果。

这些解决方案都不是完美的（特别是如果我们查看性能，或者如果我们需要非常高的精度），但它们仍然解决了二进制浮点运算的大量问题。

一些与这个著名的双精度问题相关的统计数据。

当使用 0.1（从 0.1 到 100）的步长添加所有值 (a + b) 时，我们有大约 15% 的机会出现精度误差。请注意，误差可能会导致值稍大或稍小。以下是一些示例：

0.1 + 0.2 = 0.30000000000000004 (BIGGER)
0.1 + 0.7 = 0.7999999999999999 (SMALLER)
...
1.7 + 1.9 = 3.5999999999999996 (SMALLER)
1.7 + 2.2 = 3.9000000000000004 (BIGGER)
...
3.2 + 3.6 = 6.800000000000001 (BIGGER)
3.2 + 4.4 = 7.6000000000000005 (BIGGER)

当使用 0.1 的步长（从 100 到 0.1）减去所有值（a – bwherea > b）时，我们有大约 34% 的精度误差机会。以下是一些示例：

0.6 - 0.2 = 0.39999999999999997 (SMALLER)
0.5 - 0.4 = 0.09999999999999998 (SMALLER)
...
2.1 - 0.2 = 1.9000000000000001 (BIGGER)
2.0 - 1.9 = 0.10000000000000009 (BIGGER)
...
100 - 99.9 = 0.09999999999999432 (SMALLER)
100 - 99.8 = 0.20000000000000284 (BIGGER)

*15% 和 34% 确实很大，因此当精度非常重要时，请始终使用 BigDecimal。如果使用 2 个小数位（步长 0.01），情况会更糟一些（18% 和 36%）。

从 Python 3.5 开始，您可以使用math.isclose()函数来测试近似相等：

>>> import math
>>> math.isclose(0.1 + 0.2, 0.3)
True
>>> 0.1 + 0.2 == 0.3
False

已经发布了很多好的答案，但我想再附加一个。

并非所有数字都可以通过浮点数/双精度数表示，例如，数字“0.2”将在 IEEE754 浮点标准中以单精度表示为“0.200000003”。

引擎盖下存储实数的模型将浮点数表示为

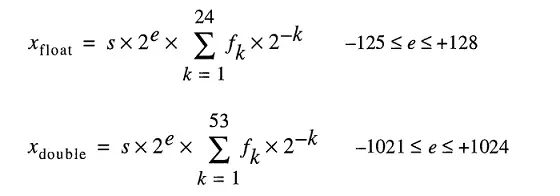
即使您可以轻松输入0.2，FLT_RADIX和DBL_RADIX是2；对于使用“二进制浮点算术的 IEEE 标准 (ISO/IEEE Std 754-1985)”的 FPU 计算机，不是 10。

所以要准确地表示这些数字有点困难。即使您在没有任何中间计算的情况下明确指定此变量。

我的解决方法：

function add(a, b, precision) {
    var x = Math.pow(10, precision || 2);
    return (Math.round(a * x) + Math.round(b * x)) / x;
}

精度是指在加法过程中要在小数点后保留的位数。

我可以添加吗？人们总是认为这是一个计算机问题，但如果你用手数（以 10 为底），你不能得到(1/3+1/3=2/3)=true，除非你有无穷大将 0.333.. 加到 0.333..。所以就像(1/10+2/10)!==3/10问题在基数 2 中，您将其截断为 0.333 + 0.333 = 0.666 并可能将其四舍五入为 0.667，这在技术上也是不准确的。

以三进制数数，但三分之二不是问题 – 也许一些每只手有 15 个手指的比赛会问为什么你的十进制数学被打破了……

普通算术是以 10 为基数的，因此小数表示十分位、百分之一等。当您尝试在二进制基数为 2 的算术中表示浮点数时，您正在处理一半、四分之一、八分之一等。

在硬件中，浮点数存储为整数尾数和指数。尾数表示有效数字。指数类似于科学计数法，但它使用 2 而不是 10 的底数。例如 64.0 将用尾数 1 和指数表示6。 0.125 将用尾数 1 和指数 -3 来表示。

浮点小数必须加起来 2 的负幂

0.1b = 0.5d
0.01b = 0.25d
0.001b = 0.125d
0.0001b = 0.0625d
0.00001b = 0.03125d

等等。

在处理浮点运算时，通常使用错误增量而不是使用相等运算符。代替

if(a==b) ...

你会用

delta = 0.0001; // or some arbitrarily small amount
if(a - b > -delta && a - b < delta) ...